Il problema del massimo flusso in una rete
Il problema del massimo flusso consiste nel massimizzare il flusso da un nodo sorgente s a un nodo destinazione t in un grafo orientato (digrafo).
E' uno dei problemi tipici della ricerca operativa.
Spiegazione
Ho una rete R composta da un insieme N di nodi e un insieme A di archi.
$$ R = ( N, A, b, u ) $$
- La variabile b è un vettore delle forniture/domande che indica per ogni nodo il flusso netto x ( uscita-entrata ).
- La variabile u è un vettore della capacità massima del flusso in ogni arco (i,j) di A della rete.
Ogni arco (i,j) di A può veicolare x(i,j) quantità.
Se la quantità uscente dal nodo sorgente (s) è la quantità V, il problema del massimo flusso consiste nel far arrivare -V al nodo terminale (t).
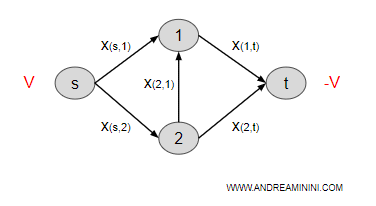
Ovviamente, il flusso deve rispettare tutti i vincoli del problema.
Posso scrivere il problema del massimo flusso come modello di programmazione lineare.
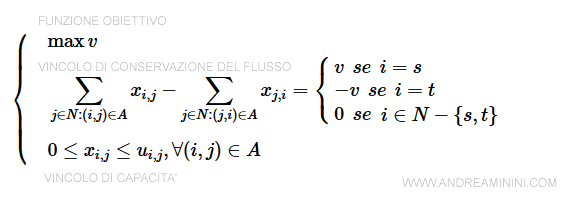
La funzione obiettivo max v massimizza il flusso netto uscente (v) dal nodo sorgente.
Il primo vincolo è il vincolo di conservazione del flusso, in base al quale il nodo sorgente ha una fornitura v e il nodo terminale una domanda -v.
Tutti gli altri nodi di transito e intermedi della rete hanno una quantità in entrata pari a quella in uscita.
L'ultimo vincolo è il vincolo di capacità che limita il flusso in ogni arco nell'intervallo compreso tra 0 e la capacità massima dell'arco u(i,j).
Nota. Per semplicità ipotizzo che gli archi non abbiano una capacità minima da rispettare.
Esempio
Ho la seguente rete con 4 nodi e 5 archi.
Dal nodo sorgente s esce un flusso V=6.
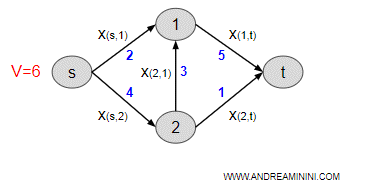
La capacità massima di ogni arco u(i,j) l'ho indicata con il colore blu.
Devo trovare il percorso Pst che massimizza il flusso dal nodo sorgente (s) al nodo terminale (t)
Nota. Scegliendo il percorso (s,1,t) trasmetto soltanto V=2 dal nodo s al nodo t. Scegliendo il percorso s-2-t soltanto V=1. Scegliendo il percorso s-2-1-t il flusso è V=3.
Esistono diversi algoritmi per risolvere questo genere di problemi.
