Algoritmo del percorso minimo in un grafo
Questo algoritmo trova il percorso ottimo, ossia un percorso di costo minimo, tra un nodo iniziale s e un nodo finale t in un grafo orientato (digrafo).
L'algoritmo è suddiviso in due fasi
- Inizializzazione
Nella prima fase l'algoritmo inizializza le variabili. - Ricerca del percoso minimo
Nella seconda fase compie N iterazioni per cercare il percorso di costo minimo (percorso ottimale) dal nodo s al nodo t.
Come funziona l'algoritmo
L'algoritmo ha i seguenti input
- un digrafo D(N,A) con N nodi e A archi
- un vettore c(i,j) dei costi degli archi
- un nodo iniziale S
Fornisce in output
- un vettore delle distanze/costi (d) ottimali da s a qualsiasi altro nodo del digrafo
- un vettore delle etichette (pred) che indica il migliore predecessore di ciascun nodo
L'elaborazione si svolge in due fasi
1] inizializzazione
| d[s]=0 | (distanza nodo iniziale=0) |
| d[i]=∞ | distanza iniziale di ogni nodo diverso da s) |
| pred[i]=i | ogni nodo ha predecessore se stesso) |
| cmin = min(cij) | minimo costo tra gli archi del digrafo) |
| L={s} | la lista dei nodi da visitare contiene il nodo s |
2] iterazione
- Finché la lista dei nodi da visitare L non è nulla
- estrarre un nodo x da visitare dalla lista L
- eliminare il nodo x dalla lista L
- aggiungere alla lista L i nodi adiacenti di x (se non già presenti in L)
- calcolare la distanza dei nodi adiacenti del nodo x d'[j]=d[x]+c(x,j)
- se ll costo d'[j]<d[j]
- aggiornare il vettore d[j]=d'[j]
- aggiornare il predecessore pred[j]=x
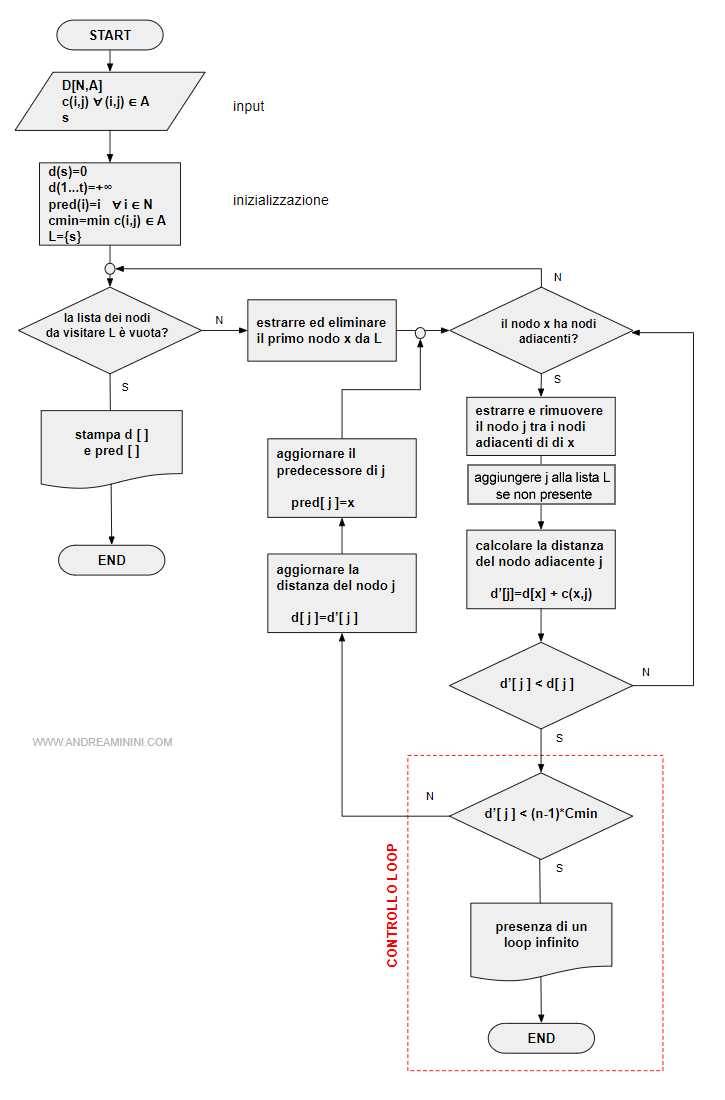
Posso descrivere l'algoritmo anche con un diagramma di flusso
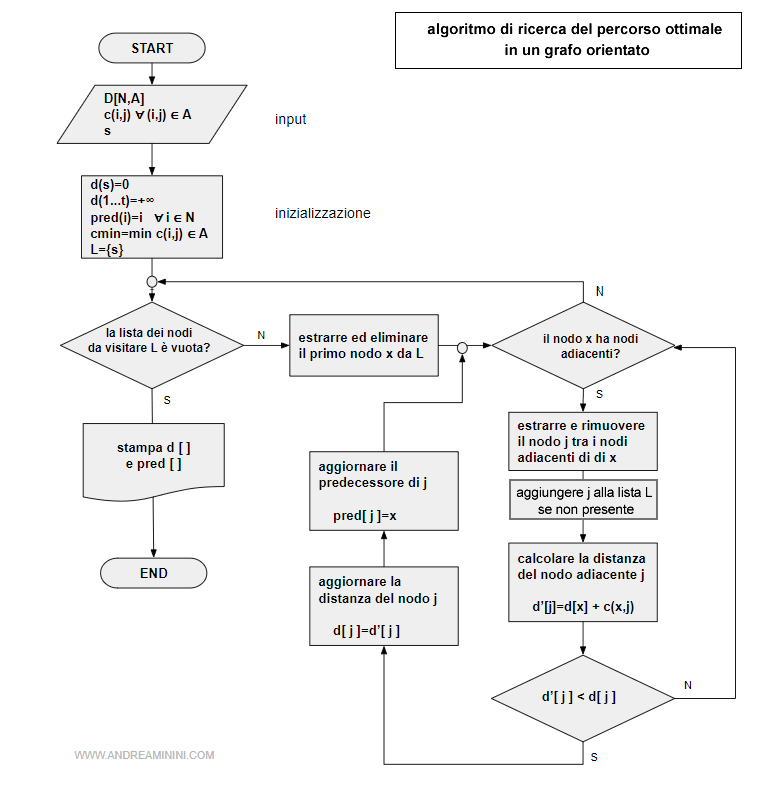
Al termine dell'esecuzione il valore d[i] indica il costo minimo del percorso per raggiungere l'i-esimo nodo a partire dal nodo iniziale S.
Se il valore d[i] è infinito, vuol dire che l'i-esimo nodo non è raggiungibile dal nodo S.
Nota. L'insieme di tutti i cammini orientati dal nodo S agli altri nodi raggiungibili del digrafo è detta arborescenza. Di fatto l'arborescenza è un sottodigrafo.
Un esempio pratico
Ho il seguente digrafo composto da 4 nodi e 5 archi.
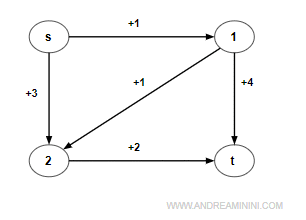
Inizializzazione
Nel vettore/lista dei nodi da visitare inserisco il nodo iniziale s.
$$ L=\{s\} $$
Il vettore delle distanze d è composto da 4 elementi, uno per ciascun nodo del digrafo.
$$ d = [ d_s , d_1 , d_2, d_t ] $$
La distanza del primo elemento (s) è posta a zero mentre le altre sono poste a infinito di default.
$$ d = [ 0 , +\infty, +\infty, +\infty ] $$
Il vettore pred individua il miglior predecessore per ciascun nodo, quello con il costo di percorso minimo.
E' composto da 4 elementi, uno per ciascun nodo del digrafo.
$$ pred = [ s , 1, 2, t ] $$
Nella fase di inizializzazione a ogni nodo è assegnato se stesso come miglior predecessore.
Individuo il costo minore negli archi del digrafo per verificare se ci sono archi con costi negativi.
$$ c_{min} = +1 $$
Un costo negativo implica il rischio di cicli infiniti nel digrafo.
In questo caso non ci sono perché cmin>0.
Iterazione 1
Estraggo un nodo dalla lista L (nodi da visitare) e lo elimino da L.
In questo caso c'è solo il nodo s.
$$ L = L \ \{s\} $$
Pertanto la lista L diventa vuota
$$ L = \{ \: \} $$
Il nodo corrente è s.
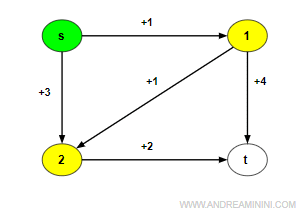
Individuo i nodi adiacenti al nodo estratto (s) ossia 1 e 2.
Li aggiungo ai nodi da visitare.
$$ L = L \: \cup \: \{1, 2 \} = \{ \: \} \cup \: \{1, 2 \} = \{1, 2 \} $$
Poi calcolo le distanze tra il nodo corrente (s) e i nodi adiacenti {1,2}.
$$ d'[1] = d_s + c(s,1) = 0 + 1 = 1 $$
$$ d'[2] = d_s + c(s,2) = 0 + 3 = 3 $$
La distanza d'[1]=1 è inferiore alla distanza d[1] =∞ nel vettore d.
$$ d = [ 0 , {\color{Red} {+\infty} } , +\infty, +\infty ] $$
Quindi, aggiorno il vettore d e assegno pred(1)=s come miglior predecessore del nodo 1.
$$ d = [ 0 , {\color{Red} 1} , +\infty, +\infty ] $$
$$ pred = [ s , {\color{Red} s}, 2, t ] $$
La distanza d'[2]=3 è inferiore alla distanza d[2] =3 nel vettore d.
$$ d = [ 0 , 1, {\color{Red} {+\infty} } , +\infty ] $$
Quindi, aggiorno il vettore d e assegno pred(2)=s come miglior predecessore del nodo 2.
$$ d = [ 0 , 1, {\color{Red} 3}, +\infty ] $$
$$ pred = [ s , s, {\color{Red} s}, t ] $$
Nota. Al termine dell'iterazione la situazione è $$ L = \{1,2 \} \:\: d = [ 0 , 1, 3, +\infty ] \:\: pred = [ s , s, s, t ] $$
Iterazione 2
Estraggo il primo nodo disponibile nella lista L. Si tratta del nodo 1.
$$ L = \{ {\color{Red} 1 } , 2 \} $$
Lo elimino dalla lista dei nodi da visitare.
$$ L = L \ \{1\} $$
Pertanto la lista L diventa
$$ L = \{ \: 2 \} $$
Il nodo corrente è il nodo 1.
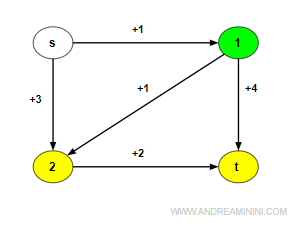
Individuo i nodi adiacenti al nodo estratto (1) ossia 2 e t.
Li aggiungo ai nodi da visitare.
$$ L = L \: \cup \: \{2, t \} = \{ \: 2 \} \cup \: \{2, t \} = \{2, t \} $$
Nota. Il nodo 2 è già presente nella lista. In questo caso non va aggiunto. Nella lista dei nodi da visitare ogni nodo deve apparire al massimo una volta. Non di più.
Sapendo che d[1]=1
$$ d = [ 0 , {\color{Red} 1 }, 3, +\infty ] $$
Calcolo le distanze d tra il nodo corrente (1) e i nodi adiacenti {2,t}.
$$ d'[2] = d[1] + c(1,2) = 1 + 1 = 2 $$
$$ d'[t] = d[1] + c(1,t) = 1 + 4 = 5 $$
Poi verifico se le nuove distanze sono migliori delle precedenti già registrate.
La distanza d'[2]=2 è inferiore alla distanza d[2] =3 nel vettore d.
$$ d = [ 0 , 1 , {\color{Red} 3 }, +\infty ] $$
Quindi, aggiorno il vettore d
$$ d = [ 0 , 1 , {\color{Red} 2 }, +\infty ] $$
e assegno pred[2]=1 come miglior predecessore del nodo 2.
$$ pred = [ s , s, {\color{Red} 1 } , t ] $$
La distanza d'[t]=5 è inferiore alla distanza d[t] =+∞ nel vettore d.
$$ d = [ 0 , 1 , 2, {\color{Red} {+\infty} } ] $$
Quindi, aggiorno il vettore d
$$ d = [ 0 , 1 , 2, {\color{Red} 5 } ] $$
e assegno pred[t]=1 come miglior predecessore del nodo 2.
$$ pred = [ s , s, 1 , {\color{Red} 1 } ] $$
Nota. Al termine dell'iterazione la situazione è $$ L = \{2,t \} \:\: d = [ 0 , 1, 2, 5 ] \:\: pred = [ s , s,1,1 ] $$
Iterazione 3
Estraggo il primo nodo disponibile nella lista L. Si tratta del nodo 2.
$$ L = \{ {\color{Red} 2, t } \} $$
Lo elimino dalla lista dei nodi da visitare.
$$ L = L \ \{ 2 \} = \{ 2,t \} \ \{ 2 \} = \{ t \} $$
Pertanto la lista L diventa
$$ L = \{ t \} $$
Il nodo corrente è il nodo 2.
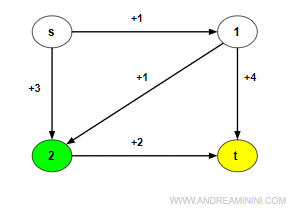
Individuo i nodi adiacenti al nodo estratto (2) ossia t.
Lo aggiungo ai nodi da visitare.
$$ L = L \: \cup \: \{t \} = \{ t \} \cup \: \{ t \} = \{ t \} $$
Nota. Il nodo t è già presente nella lista L dei nodi da visitare. Pertanto, non occorre aggiungerlo.
Sapendo che d[2]= 2
$$ d = [ 0 , 1 , {\color{Red} 2} , 5 ] $$
Calcolo le distanze d tra il nodo corrente (2) e i nodi adiacenti {t}.
$$ d'[t] = d[2] + c(2,t) = 2 + 2 = 4 $$
Poi verifico se le nuove distanze sono migliori delle precedenti già registrate.
La distanza d'[t]=4 è inferiore alla distanza d[t] =5 nel vettore d.
$$ d = [ 0 , 1 , 2 , {\color{Red} 5} ] $$
Quindi, aggiorno il vettore d
$$ d = [ 0 , 1 , 2 , {\color{Red} 4} ] $$
e assegno pred[t]=2 come miglior predecessore del nodo t.
$$ pred = [ s , s, 1, {\color{Red} 2 } ] $$
Nota. Al termine dell'iterazione la situazione è $$ L = \{t \} \:\: d = [ 0 , 1, 2, 4 ] \:\: pred = [ s , s, 1, 2 ] $$
Iterazione 2
Estraggo il primo nodo disponibile nella lista L. Si tratta del nodo t.
$$ L = \{ {\color{Red} t } \} $$
Lo elimino dalla lista dei nodi da visitare.
$$ L = L \ \{ t \} = \{ t \} \ \{ t \} = \{ \} $$
Pertanto la lista L diventa vuota
$$ L = \{ \: \} $$
Il nodo corrente è il nodo t.
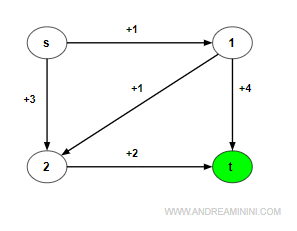
Il nodo t non ha nodi adiacenti. Pertanto, non devo aggiungere altri nodi alla lista dei nodi da visitare L.
Non essendoci nodi adiacenti, non devo nemmeno calcolare i nuovi costi del percorso.
Nota. Al termine dell'iterazione la situazione è $$ L = \{ \} \:\: d = [ 0 , 1, 2, 4 ] \:\: pred = [ s , s, 1, 2 ] $$
Iterazione 5
La lista dei nodi da visitare è vuota.
L'algoritmo termina qui.
$$ L = \{ \} $$
La situazione finale è
$$\: d = [ 0 , 1, 2, 4 ] $$
$$: pred = [ s , s, 1, 2 ] $$
Il costo minimo per raggiungere il nodo t è d[t]=4.
Per conoscere il percorso ottimale mi basta analizzare a ritroso i migliori predecessori a partire dal nodo t.
$$ pred[t]=2 \\ pred[2]=1 \\ pred[1]=s $$
Pertanto, il percorso ottimale da s a t è P*st={s,1,2,t}
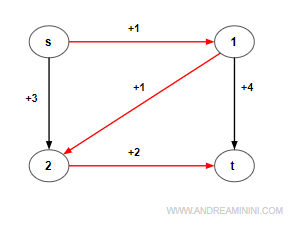
Il grafo con archi negativi
L'algoritmo di ricerca del percorso ottimale in un grafo orientato può entrare in un ciclo infinito quando gli archi hanno valori negativi.
In questo caso il problema è illimitato inferiormente.
Esempio
In questo grafo due archi sono negativi.
L'algoritmo entra in un ciclo infinito tra i nodi 1-2-t.
Nota. La presenza dei costi negativi sugli archi è una condizione necessaria ma non sufficiente all'insorgere dei cicli infiniti. Pertanto, la sola presenza di un costo negativo non vuol dire che l'algoritmo entri in un loop infinito. Ad esempio, anche questo digrafo ha due archi negativi ma non si verifica alcun loop infinito.
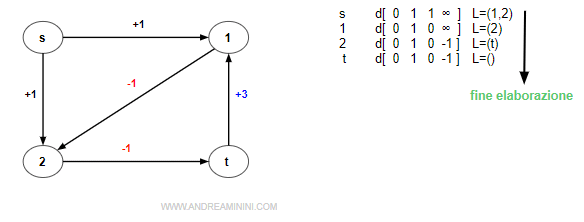
Quindi, la presenza di un costo minimo inferiore di zero (cmin<0) non causa necessariamente un loop infinito.
Come evitare il problema?
L'algoritmo va leggermente modificato con un controllo aggiuntivo.
L'elaborazione viene interrotta anticipatamente se dopo l'aggiornamento dell'etichetta di un nodo si verifica la seguente condizione
d[i]<(n-1)*cmin<0
Dove n è il numero dei nodi del digrafo mentre cmin è il costo più basso degli archi del digrafo.
L'arresto si verifica indipendentemente dal fatto che la lista dei nodi da visitare L sia vuota o meno.
Esempio
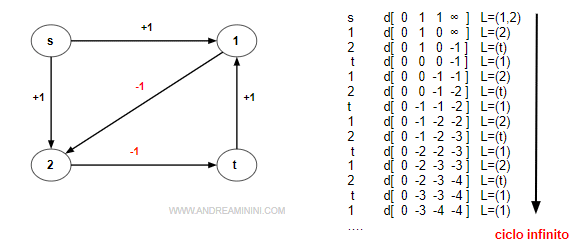
Il seguente digrafo ha un loop infinito.
Ci sono n=4 nodi e il costo minimo è cmin=-1.
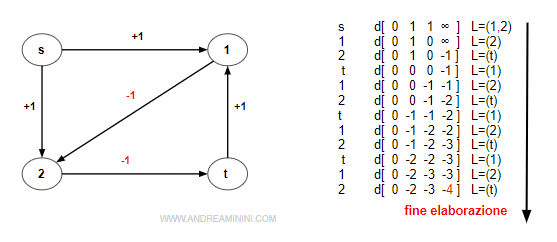
Quindi, la condizione di controllo è d[i]<(n-1)*cmin<0 ossia d[i]<-3
Grazie a questo controllo aggiuntivo l'algoritmo constata la presenza del loop dopo dodici iterazioni, quando aggiorna la distanza del nodo d[t]=-4.
In questo modo rilevo ed evito il loop infinito.
E così via.
