Algoritmo Floyd-Warshall

L'algoritmo Floyd-Warshall calcola il percorso a costo minore in un grafo orientato aciclico.

L'algoritmo prende in input un digrafo (n,m) con n nodi e m archi con i relativi costi per ciascun arco.

Restituisce in output i costi minori e i percorsi ottimi per tutte le coppie di nodi.

Nota. A differenza di altri algoritmi non calcola il percorso ottimo da un nodo di partenza (sorgente) a un nodo finale (pozzo) bensì da qualsiasi nodo a qualsiasi altro nodo del grafo. E' quindi un'informazione molto più completa.

Come funziona

Nella fase di inizializzazione crea due matrici nxn.

• La prima matrice misura i costi minimi tra due nodi (da,a) in ogni percorso
• La seconda matrice indica i predecessori (da) di ciascun nodo (a) in ogni percorso possibile.

Nota. Nella matrice dei costi sono posti a zero le celle della diagonale principale d(i,i)=0. Le celle non associate a un arco sono di default pari a +∞.

Nella fase di elaborazione un'iterazione esterna legge un nodo alla volta k=1,....,n.

Poi cerca i percorsi P(i,j) in cui il nodo k è un nodo intermedio.

Una volta trovati i percorsi P(i,j) verifica se la somma dei costi dei sottopercorsi d(i,k)+d(k,j) è inferiore al costo d(i,j). Se è inferiore l'algoritmo aggiorna le seguenti etichette

• d(i,j) = d(i,k)+d(k,j)
• pred(i,j) = pred(k,j)

Come verificare se il grafo contiene un ciclo? Se il grafo contiene un ciclo, almeno una cella della diagonale principale nella matrice dei costi è inferiore a zero d(i,i)<0. In fase di inizializzazione è stato posto d(i,i)=0. Quindi, se d(i,i) diventa negativo, l'unica causa possibile è la presenza di un ciclo con archi negativi all'interno del grafo.

Un esempio pratico

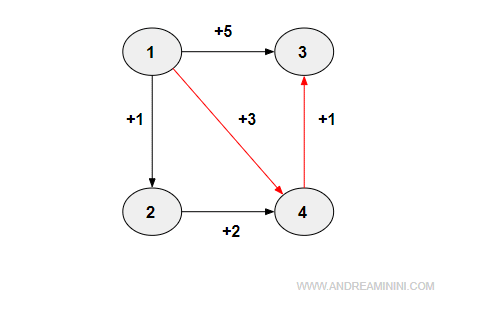
Per spiegare meglio il funzionamento dell'algoritmo faccio un esempio pratico.

Questo semplice grafo orientato ha n=4 nodi.

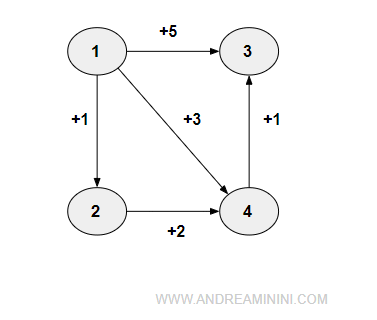
Per prima cosa l'algoritmo esegue l'inizializzazione.

Poi segue la fase di elaborazione dei nodi.

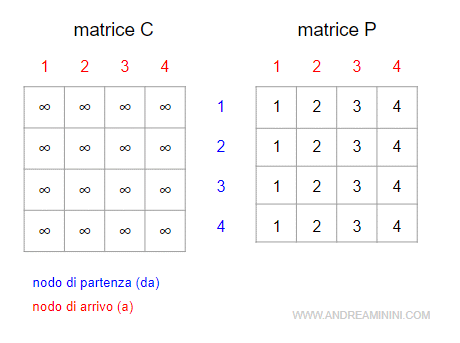
Fase di inizializzazione

Nella fase di inizializzazione l'algoritmo crea due matrici quadrate n x n:

• la matrice C dei costi di spostamento sugli archi
• la matrice P dei predecessori dei nodi

Di default la matrice C dei costi ha tutti valori infiniti ∞ mentre la matrice P è composta dai nodi da 1 a n ripetuti in ogni riga.

Per ciascun nodo da 1 a n l'algoritmo individua gli archi uscenti scrivendo i costi e il nodo predecessore nelle due matrici C e P.

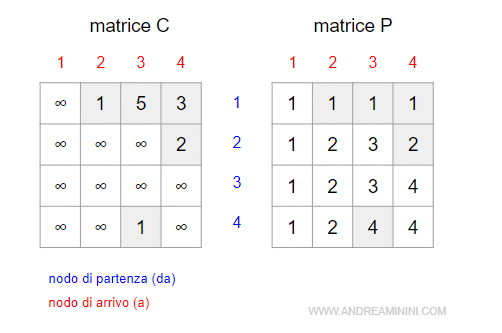
Spiegazione. Il nodo 1 ha tre archi uscenti (1,2), (1,3) e (1,4) con rispettivi costi +1, +5 e +3. Nella matrice C l'algoritmo aggiorna i costi nelle rispettive celle C(1,2) = +1, C (1,3) = +5, C(1,4) = +3. Nella matrice P viene aggiornato il predecessore P(1,2) = 1, P(1,3) = 1, P(1,4) = 1. Il nodo 2 ha un solo arco in uscita (2,4) con costo pari a +2. Nella matrice C viene aggiornata la cella C(2,4)=2 e nella matrice P il predecessore P(2,4)=2. Il nodo 4 ha un solo arco in uscita (4,3). Quindi, l'algoritmo aggiorna il costo C(4,3)=2 e il predecessore P(4,3)=4.

Durante l'iterazione da 1 a n l'algoritmo inserisce il valore zero nella matrice C dei costi se il numero della colonna è uguale al numero della riga.

In pratica azzera i valori sulla diagonale principale della matrice C.

Tutto è pronto per passare alla fase di elaborazione.

Nota. La fase di inizializzazione ha complessità pari a O(n) perché l'algoritmo deve leggere gli n nodi del grafo per modificare i valori delle due matrici quadrate. In questo esempio n=4 perché il grafo ha quattro nodi.

Fase di elaborazione

L'algoritmo itera i nodi da k=1,...,4 per verificare se sono nodi intermedi di qualche percorso P(da,a).

Quando trova un percorso P(da,a) verifica se la somma dei costi dei sottopercorsi C(da,k)+C(k,a) è inferiore al costo del percorso C(da,a). Se è inferiore aggiorna le etichette C e P con i nuovi dati

C(da,a) = C(da,k)+C(k,a)

P(da,a) = P(k,a)

Nodo 1

Il primo nodo da elaborare è il nodo 1.

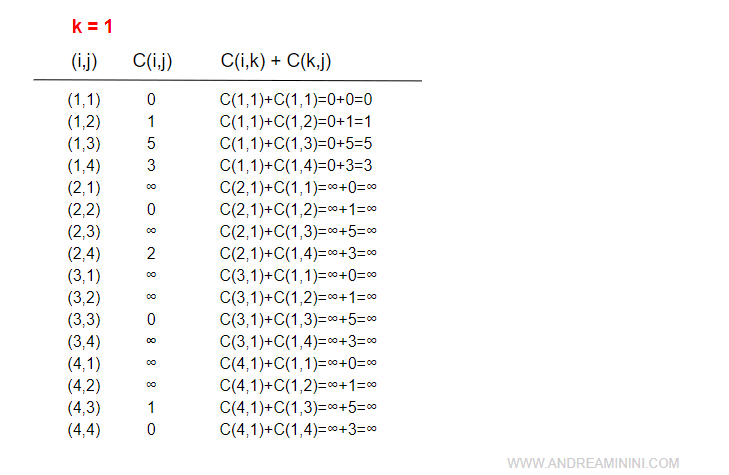
Il nodo k=1 non è un nodo intermedio dei percorsi perché, salvo i casi banali iniziali, i costi dei sottopercorsi sono uguali infinito.

Quindi, non c'è nessun aggiornamento da fare.

Nodo 2

Il secondo nodo da analizzare è il nodo 2.

Anche in questo caso non c'è nessun nodo da aggiornare.

Nodo 3

Il terzo nodo da analizzare è il nodo 3.

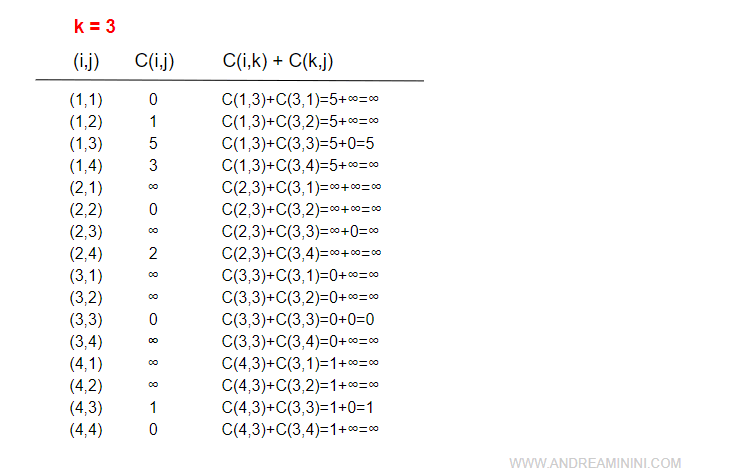
Non ci sono nodi da aggiornare.

Nodo 4

Il quarto nodo da elaborare è il nodo k=4.

Il percorso (1,3) include il nodo k=4 perché i costi dei sottopercorsi sono numeri interi C(1,4)+C(4,3)=3+1.

Inoltre, la somma dei costi dei sottopercorsi C(1,4)+C(4,3)=4 è inferiore al costo del percorso C(1,3)=5

Quindi l'algoritmo aggiorna l'etichetta C(1,3)=4 e l'etichetta P(1,3)=P(1,4)=4.

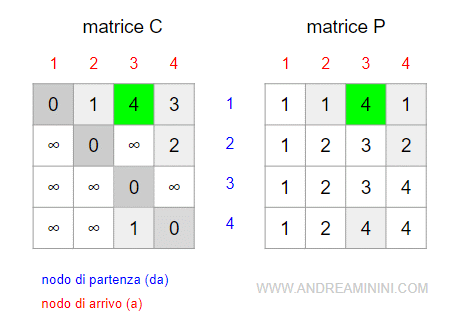
C'è anche un altro aggiornamento da fare. Il percorso (2,3) include il nodo k=4 e la somma dei costi dei sottopercorsi C(2,4)+C(4,3)=2+1 è inferiore al costo del percorso C(2,3)=∞.

Quindi l'algoritmo aggiorna l'etichetta C(2,3)=3 e l'etichetta P(2,3)=P(4,3)=4.

Nota. Questa operazione ha una complessità k x ( n x n ). Peranto, essendo k=n, la complessità è O(n³).

L'algoritmo restituisce in output le matrici C e P ottimizzate per i percorsi ottimi da qualsiasi nodo a un altro.

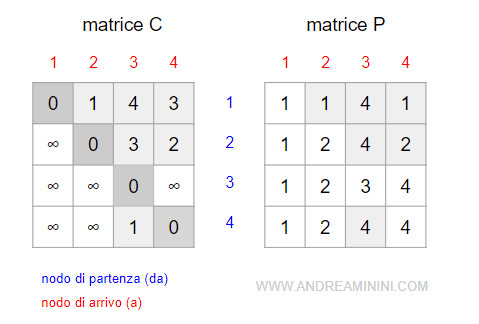
Ad esempio, per andare dal nodo 1 al nodo 3 la matrice C mi permette di conoscere il costo del percorso ottimo C(1,3)=4.

La matrice P, invece, mi permette di trovare i predecessori a partire dal nodo finale.

P(1,3)=4
P(1,4)=1

Quindi, il percorso migliore per andare dal nodo 1 al nodo 3 è il seguente: 1 , 4, 3.

L'algoritmo Floyd-Warshall su Python

Ecco un semplice sviluppo in Python dell'algoritmo di Floyd-Warshall.

1. import numpy as np
2. grafo=np.array([[0,1,5,3],[None,0,None,2],[None,None,0,None],[None,None,1,0]])
3. pred=np.array([[1, 1, 1, 1],[1, 2, 3, 2],[1, 2, 3, 4],[1, 2, 4, 4]])
4. # numero nodi nel grafo
5. n=grafo.shape[0]
6. # inizializzazione
7. for i in range(0,n):
8. grafo[i,i]=0
9. pred[i,i]=i+1
10. # elaborazione
11. for k in range(1,n+1):
12. print(" k = ", k)
13. for riga in range(1,n+1):
14. for colonna in range(1, n+1):
15. d=grafo[riga-1,colonna-1]
16. ds=None
17. if ((grafo[riga-1,k-1]!=None)&(grafo[k-1, colonna-1]!=None)):
18. ds=grafo[riga-1,k-1]+grafo[k-1, colonna-1]
19. if (ds!=None):
20. if (d==None):
21. grafo[riga-1,colonna-1]=ds
22. pred[riga-1,colonna-1]=pred[k-1,colonna-1]
23. else:
24. if (d>ds):
25. grafo[riga-1,colonna-1]=ds
26. pred[riga-1,colonna-1]=pred[k-1,colonna-1]
27. print("*********************")
28. print(grafo)
29. print("*********************")
30. print(pred)

E così via.