Esercizio sul problema del massimo flusso in un grafo tramite PL

Un grafo è composto da 8 nodi e archi con vincoli di capacità. Devo calcolare il massimo flusso come problema di programmazione lineare (PL). Tutti gli archi non indicati espressamente nel problema sono considerarsi con capacità nulla.

Archi	Capacità
(s,1)	6
(s,5)	3
(1,4)	5
(1,3)	9
(2,5)	3
(2,t)	6
(3,6)	2
(4,5)	4
(4,2)	6
(5,1)	5
(5,6)	2
(6,2)	7
(6,t)	2

Per prima cosa costruisco il grafo.

Si tratta di un grafo orientato.

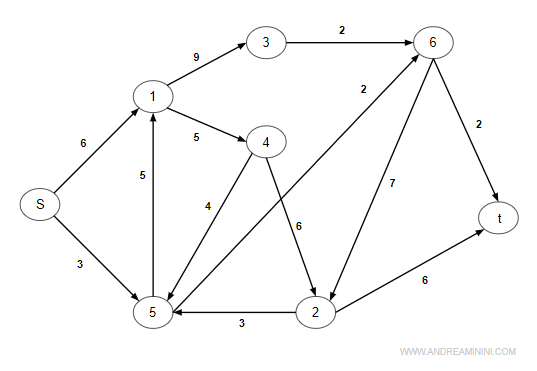
Le variabili del problema sono le quantità di flusso passanti da un nodo a un altro.

Ad esempio x_s1 indica il flusso da s a 1

Le altre variabili sono x_s2, x₁₂, x₁₃, x₂₃, x_2t, x₃₄, x₃₆, x₄₂, x₄₃, x₅₂, x₅₄, x_6t^, x_ts.

Nota. Per indicare le variabili ho combinato in pedice il nodo di partenza (da) e di arrivo (a). $$ x_{da a} $$ Pertanto, la variabile x₁₃ indica il flusso sull'arco dal nodo 1 al nodo 3.

Tutte le variabili sono maggiori o uguali a zero (non negative).

$$ x \ge 0 $$

Ogni variabile deve rispettare anche il vincolo di capacità del proprio arco.

$$ x_{s1} \le 6 \\ x_{s5} \le 3 \\ x_{13} \le 9 \\ x_{14} \le 5 \\ x_{25} \le 3 \\ x_{2t} \le 6 \\ x_{36} \le 2 \\ x_{45} \le 4 \\ x_{42} \le 6 \\ x_{51} \le 5 \\ x_{56} \le 2 \\ x_{62} \le 7 \\ x_{6t} \le 2 $$

Sono le variabili e i primi vincoli del sistema lineare che sto costruendo.

Ora aggiungo un arco virtuale di massimo carico da t a s con capacità infinita.

E ovviamente aggiungo nel sistema lineare anche un'altra variabile x_ts non negativa (x_ts>0).

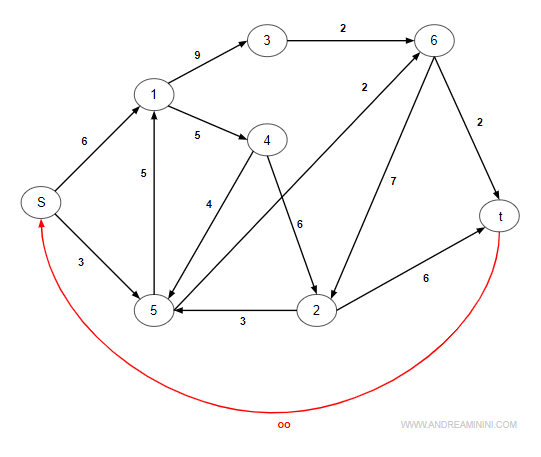
Il problema del massimo flusso da t a s consiste nella massimizzazione della variabile x_ts

Quindi, la funzione obiettivo del sistema di programmazione lineare è la seguente

$$ max \: x_{ts} $$

Per ultimare il sistema devo soltanto aggiungere i vincoli di equilibrio del flusso.

A ogni nodo associo un vincolo di equilibrio del flusso.

A cosa serve?. In pratica, in ogni nodo il flusso in entrata è uguale al flusso in uscita. Non può esserci né riduzione, né incremento del flusso.

Ad esempio, il nodo s ha un arco in entrata (x_ts) e due archi in uscita (x_s1, x_s5).

Pertanto, il vincolo di equilibrio del flusso è

$$ x_{ts} - x_{51} - x_{s5} = 0 $$

Per il nodo 1 il vincolo di equilibrio del flusso è

$$ x_{s1} + x_{s1} - x_{14}- x_{13} = 0 $$

Per il nodo 2

$$ x_{42} + x_{62} - x_{25}- x_{2t} = 0 $$

Per il nodo 3

$$ x_{13} - x_{36} = 0 $$

Per il nodo 4

$$ x_{14} - x_{42}- x_{45} = 0 $$

Per il nodo 5

$$ x_{45}+x_{25}+x_{s5} - x_{51}- x_{56} = 0 $$

Per il nodo 6

$$ x_{36} + x_{56} - x_{62}- x_{6t} = 0 $$

Arrivato a questo punto ho tutti gli elementi per costruire il sistema di programmazione lineare.

$$ max \: x_{ts} $$

$$ \begin{cases} x_{ts} - x_{s1} - x_{s5} = 0 \\ x_{s1} + x_{51} - x_{14}- x_{13} = 0 \\ x_{42} + x_{62} - x_{25}- x_{2t} = 0 \\ x_{13} - x_{36} = 0 \\ x_{14} - x_{42}- x_{45} = 0 \\ x_{45}+x_{25}+x_{s5} - x_{51}- x_{56} = 0 \\ x_{36} + x_{56} - x_{62}- x_{6t} = 0 \\ x_{s1},x_{s5},x_{13},x_{14}, x_{25}, x_{2t}, x_{36}, x_{42}, x_{45},x_{51}, x_{56},x_{62}, x_{6t} \ge 0 \\ x_{s1} \le 6 \\ x_{s5} \le 3 \\ x_{13} \le 9 \\ x_{14} \le 5 \\ x_{25} \le 3 \\ x_{2t} \le 6 \\ x_{36} \le 2 \\ x_{45} \le 4 \\ x_{42} \le 6 \\ x_{51} \le 5 \\ x_{56} \le 2 \\ x_{62} \le 7 \\ x_{6t} \le 2 \end{cases} $$

A questo punto risolvo il problema lineare con l'algoritmo del simplesso.

E così via.