I grafi
Un grafo è una struttura relazionale formata da un numero finito V di vertici ( o nodi ) e un numero finito E di segmenti ( archi o spigoli ) che collegano ogni nodo agli altri.
Un esempio pratico di grafo
Ecco un esempio pratico di grafo
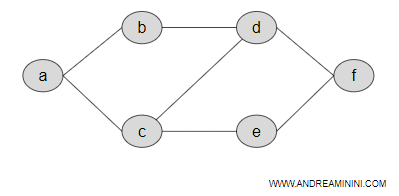
Definizione matematica di grafo
Un grafo è una relazione n-aria su un insieme finito S definita dai sottoinsiemi di S con n elementi che soddisfano una proprietà P(1,...,n).
La definizione matematica è sempre un po' difficile per spiegare un concetto informatico, quindi proverò a descrivere il concetto di grafo anche in modo pratico.
Per indicare un grafo utilizzo la notazione seguente:
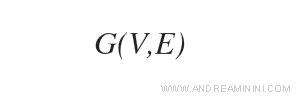
Dove V è l'insieme di tutti i nodi e E è l'insieme di tutti gli archi del grafo.
I nodi del grafo
L'insieme dei nodi è indicato con la notazione
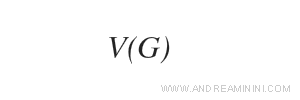
Esempio
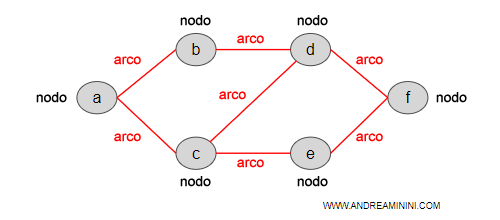
Riprendendo il grafo precedente appartengono a V(G) tutti i nodi a, b, c, d, e, f.
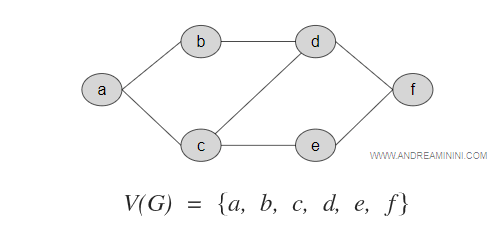
Il numero dei nodi determina l'ordine del grafo.
Gli archi del grafo
Un arco è una relazione binaria tra due nodi ed è indicato nel seguente modo:
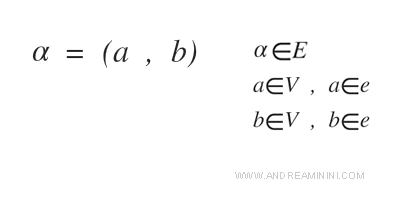
Dove a e b sono due nodi V del grafo e sono detti estremi dell'arco.
L'arco tra due vertici è detto incidente.
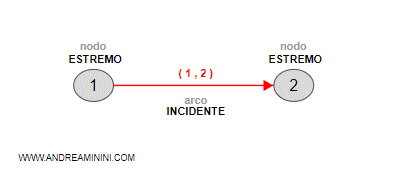
Ogni relazione forma una coppia ordinata se è indicata una direzione oppure una coppia non ordinata.
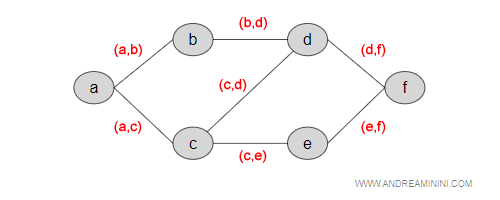
Differenza tra coppie ordinate e non ordinate. Nel caso delle coppie non ordinate, le coppie (a,b) e (b,a) indicano lo stesso spigolo del grafo. Viceversa, nel caso delle coppie ordinate le coppie (a,b) e (b,a) indicano un verso differente sullo stesso spigolo, rispettivamente a→b e b→a.
In alternativa, posso indicare un arco scrivendo soltanto i due nodi.
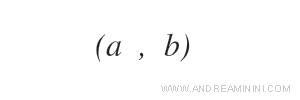
Per indicare l'insieme di tutti gli archi del grafo utilizzo la seguente notazione
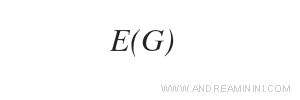
Il numero degli archi determina la dimensione del grafo.
Esempio
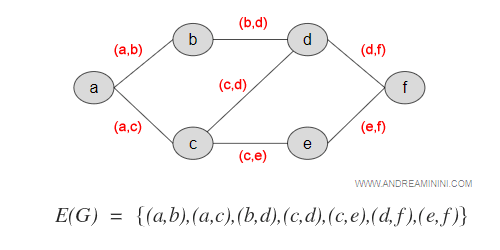
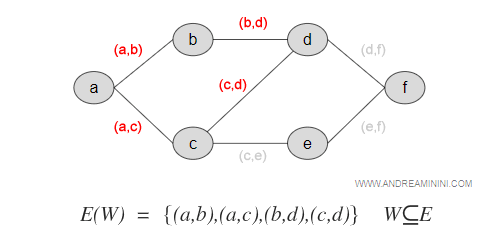
Nel grafo precedente l'insieme E(G) è composto da tutte le coppie ordinate (a,b) , (a,c), (b,d), (c,d), (c,e), (d,f), (e,f).
Posso anche indicare soltanto un sottoinsieme W del grafo.
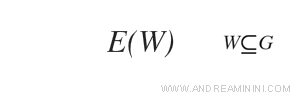
In questo caso l'insieme E(W) comprende tutti gli archi che hanno entrambi gli estremi nel sottoinsieme W.
Esempio
Il sottoinsieme W è composto soltanto dagli archi (a,b), (a,c), (b,d), (c,d).
I grafi orientati e non orientati
Esistono due categorie principali di grafi: orientati e non orientati.
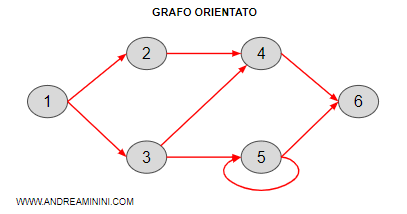
- Grafo orientato. I grafi orientati hanno gli archi con una direzione. In questo caso gli archi sono frecce. Ad esempio, si può andare dal nodo 1 al nodo 2 ma non viceversa, non si può passare dal nodo 2 al nodo 1.
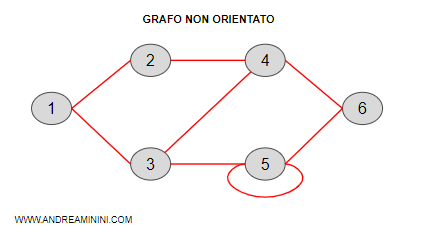
- Grafo non orientato. I grafi non orientati hanno gli archi con una relazione biunivoca tra i nodi. In altri termini, il nodo 1 collega il nodo 2 e il nodo 2 collega il nodo 1. Si può scorrere in entrambe le direzioni.
La differenza tra grafi orientati e non orientati è importante nello sviluppo dell'algoritmo di calcolo per elaborare la rete dei nodi del grafo, perché la complessità dell'algoritmo è molto diversa.
Le liste e le matrici di adiacenze
Per sviluppare un grafo in un programma informatico si utilizzano due metodi.
- La lista di adiacenze. I nodi del grafo sono memorizzati in una variabile array. Ogni elemento dell'array indica un nodo del grafo e contiene la lista delle sue connessioni ( archi ).
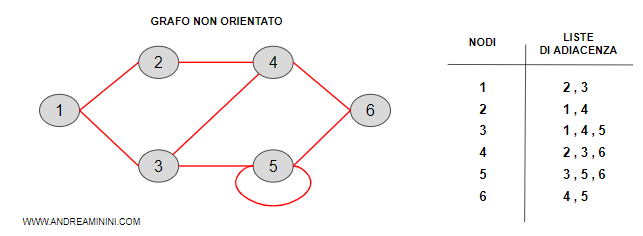
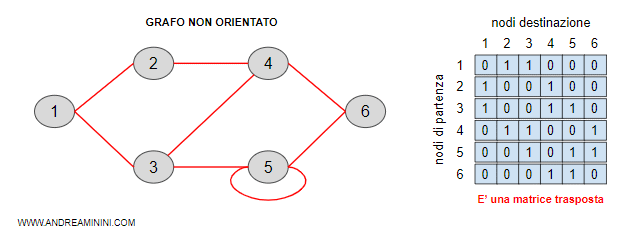
- La matrice di adiacenze. In nodi e gli archi sono memorizzati in una matrice quadrata nxn. Dove le n righe indicano i nodi di origine e le n colonne quelli di destinazione. Ogni elemento della matrice indica se i due nodi sono collegati tra loro (1) oppure no (0).