La complessità degli algoritmi
L'esecuzione di un programma implica un costo economico, dovuto all'utilizzo delle risorse ( memoria, traffico sulla rete, spazio su disco, ecc. ) e di tempo di elaborazione. In genere si parla di
- Complessità spaziale per intendere l'utilizzo delle risorse da parte di un programma.
- Complessità temporale per intendere il tempo di esecuzione di un programma.
Nello sviluppo di un algoritmo è particolarmente importante la complessità temporale.
Nota. La complessità spaziale è spesso compensata dai progressi tecnologici sui componenti hardware del computer ( es. hard disk e memorie ram più capienti ).
La complessità temporale
La complessità temporale cresce al crescere della dimensione n dei dati in input.
Per dimensione dell'input intendo la quantità dei dati in input di un algoritmo.
Il tempo di esecuzione di un algoritmo è strettamente legato al funzionamento di un algoritmo.
Per raggiungere un obiettivo esistono algoritmo più efficienti di altri.
Esistono anche altri fattori che possono influenzare il tempo di esecuzione ma in un'analisi dell'algoritmo non vanno considerati.
Esempio. Nel computo della complessità di un algoritmo non vanno considerati gli aspetti hardware, la velocità del processore (cpu), né le tecniche di compilazione, il compilatore o il linguaggi di programmazione utilizzato.
L'analisi asintotica
In informatica per calcolare la complessità computazionale di un algoritmo si utilizza l'analisi asintotica.
Tuttavia, l'analisi asintotica è uno strumento della matematica che si applica alle funzioni, mentre il tempo di esecuzione non lo è.
Quindi, per usare l'analisi asintotica devo trasformare il tempo di esecuzione dell'algoritmo in una funzione T(n) in funzione della dimensione n dei dati input.
In genere la funzione T(n) misura il numero di comandi eseguiti dall'algoritmo.
Data un'istanza di dimensione n, nel caso peggiore l'algoritmo ha una complessità temporale O(f(n)) se T(n)=O(f(n)).
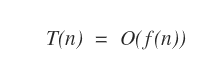
Dove n è il numero delle righe eseguite ( dimensione n dei dati ) mentre f(n) è un limite superiore del tempo di esecuzione dell'algoritmo nell'ipotesi peggiore.
Nell'analisi asintotica il simbolo O è detto "o grande".
Nota. Oltre a O grande si utilizzano anche le altre notazioni del calcolo asintotico, ossia omega (Ω) e theta (θ). In questo appunto mi limito ad accennare la loro esistenza per non appesantire la spiegazione. La differenza tra O, Ω e θ è la delimitazione superiore, inferiore o media della funzione T(n). Per approfondire la differenza rimando alla lettura del calcolo asintotico.
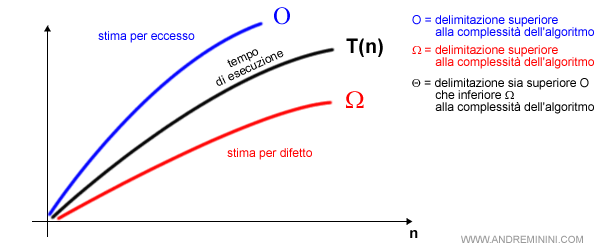
In ogni caso, per valutare la complessità di un algoritmo si utilizza sempre l'ipotesi del caso peggiore.
Perché si utilizza il caso peggiore?
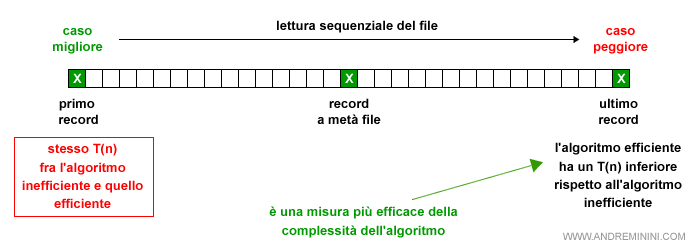
Faccio un esempio pratico, un algoritmo cerca sequenzialmente un dato X in un file composto da 1000 record, partendo dal primo all'ultimo.

Possono verificarsi tre casi:
- Caso migliore. Il dato X si trova al primo record (1 iterazione).
- Caso intermedio. Il dato X si trova alla metà del file (500 iterazioni).
- Caso peggiore. Il dato X si trova alla fine del file (1000 iterazioni). Per arrivarci l'algoritmo deve leggere tutto il file.
Nell'analisi di un algoritmo si utilizza il caso peggiore, perché è quello che ne misura meglio l'efficienza dal punto di vista tecnico.
Viceversa, il caso migliore non permette di distinguere un algoritmo inefficiente da uno efficiente.
Nota. A volte il caso medio è utile se l'algoritmo deve essere eseguito moltissime volte perché il caso peggiore e quello migliore si compensano tra loro nel corso del tempo. E' comunque preferibile analizzare sempre anche il caso peggiore, perlomeno per evitare il rischio di sviluppare un "algoritmo eterno".
Come calcolare la complessità di un algoritmo
Il seguente pseudocodice è composto soltanto da 6 linee.
Tuttavia nel codice sono presenti due cicli nidificati.

Nota. Per semplicità uso lo stesso costo c per ogni istruzioni. In realtà, il costo computazionale varia a seconda se si tratta di un'assegnazione, di un confronto, ecc. Inoltre, per semplicità sto utilizzando uno pseudocodice. Un algoritmo scritto in pseudocodice può comunque essere implementato in un programma utilizzando qualsiasi linguaggio di programmazione.
L'algoritmo prende in input un vettore M composto da 5 elementi ( length=5 ).
Poi verifica se esistono elementi uguali all'interno del vettore.
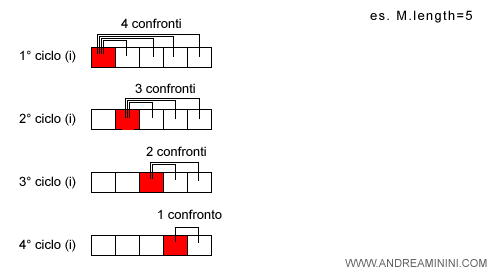
Nota. Il ciclo più esterno non analizza l'ultimo elemento perché non ha alcun elemento successivo. Quindi, il ciclo va dal primo al penultimo elemento. Il ciclo più interno, invece, prende in considerazione soltanto gli elementi successivi a quello di riferimento (i) per evitare di ripetere gli stessi confronti più volte.
Per calcolare la complessità devo calcolare quante volte (n) ogni riga di codice viene eseguita.
La prima linea (1) e l'ultima (2) sono eseguite una sola volta durante l'esecuzione del programma (n=1).

Il calcolo si complica un po' quando devo analizzare i cicli.
Il ciclo esterno
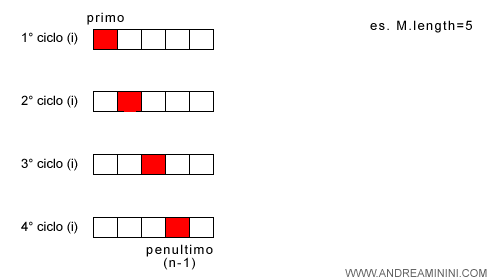
La seconda linea del codice è un'iterazione for che va dal primo elemento del vettore (i=0) al penultimo (i=length-2) ossia 5-2=3 ( incluso ).
Attenzione. Negli array il primo elemento dell'array ha sempre l'indice uguale a 0. Quindi l'ultimo elemento del vettore M non è M[5] ma M[4]. E' opportuno non confondersi.
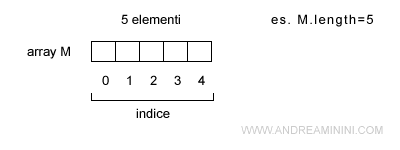
Quindi, il ciclo compie n-1 iterazioni dove n=5.
Tuttavia, per calcolare la complessità devo considerare anche il test di chiusura del ciclo.
La riga di codice viene eseguita anche quando la condizione (i≤M.length) non viene soddisfatta e il programma esce dall'iterazione.
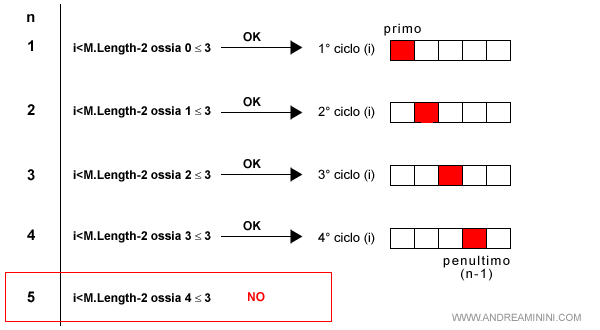
Pertanto, la seconda linea del codice viene eseguita (n-1)+1 volte ossia n volte.
A questo punto scrivo n nella colonna vicino alla riga di codice.

Il ciclo interno
Nella linea 3 c'è il secondo ciclo interno (j) che analizza gli elementi del vettore a partire dalla posizione i+1 fino all'ultimo length-1 ( compreso ) ossia n-1.
Attenzione. Come nel precedente caso n-1 indica l'ultimo elemento dell'array. L'array è composto da 5 elementi (n=5) ma il primo elemento parte dalla posizione zero (M[0]). Pertanto l'ultimo elemento è M[4] ossia n-1=4.

Quindi, compie n-(i+1) iterazioni ossia n-i-1 uterazioni per ogni i dove n=5.
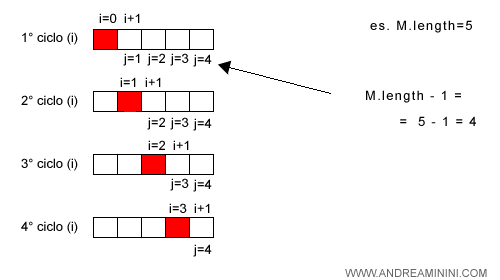
Anche in questo caso va considerato anche l'ulteriore confronto di chiusura.
Pertanto, la terza riga del codice viene eseguita (n-i-1)+1 volte ossia n-i volte per ogni i.
Ma quante volte varia i?
Guardando il ciclo esterno l'indice i varia da 0 a n-2.
Quindi per calcolare il numero di volte che viene eseguito il ciclo interno devo calcolare la seguente sommatoria.

Per semplificare il calcolo scorporo la sommatoria in due distinti elementi:
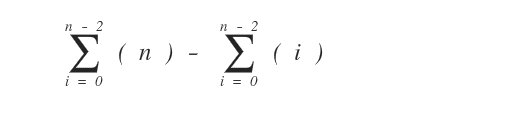
Poi risolvo le due sommatorie singolarmente, generalizzando il numero delle esecuzioni per n.
La prima componente viene eseguita n(n-1) volte.
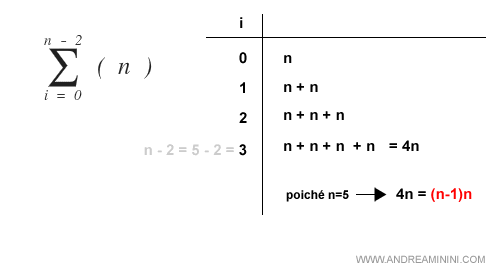
La seconda componente viene eseguita (n-2)(n-1)/2 volte secondo la formula di Gauss delle serie divergenti.

Poi sommo tutte le componenti tra loro e svolgo i relativi passaggi algebrici.
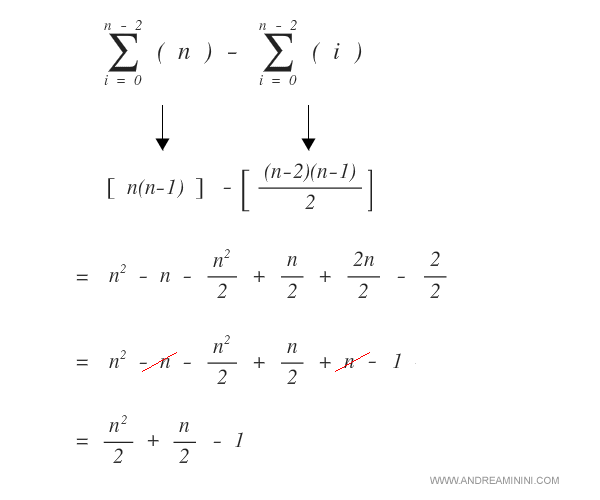
La linea 3 del ciclo interno viene eseguita 0.5n2 + 0.5n - 1 volte
Ma anche in questo caso devo aggiungere l'ultimo confronto di uscita della for.
Quindi, la linea 3 viene eseguita 0.5n2 + 0.5n volte

La linea 4 viene eseguita ogni iterazione del ciclo interno (salvo il confronto finale di uscita).
Quindi la linea 4 viene eseguita 0.5n2 + 0.5n - 1 volte.

Infine, la linea 5 viene eseguita ogni volta che M[i]=M[j] è soddisfatta (linea 4).
Tuttavia, io non so esattamente quante volte accade.
In questi casi nel calcolo della complessità di un algoritmo si utilizza l'ipotesi peggiore ossia in tutte le iterazioni del ciclo interno.
Secondo questa ipotesi la linea 5 è eseguita 0.5n2 + 0.5n - 1 volte.

A questo punto devo moltiplicare il numero di esecuzione di ciascun riga per il suo costo (c).
In questo caso è facile perché ho ipotizzato lo stesso costo c per tutte le istruzioni.

Poi sommo tutti i costi di esecuzione delle linee.
Ottengo così il costo finale dell'elaborazione.

Per calcolare la complessità dell'algoritmo devo prendere in considerazione l'elemento più significativo ossia n2 senza considerare il coefficiente ( 1.5 ).
Gli altri dati possiamo ignorarli perché non sono rilevanti
Esempio. E' inutile considerare gli altri elementi ( 2.5n ) perché influenzerebbero ben poco il risultato finale.
Quindi la complessità computazionale dell'algoritmo è O(n2).
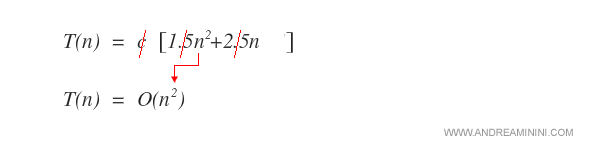
Un metodo alternativo
C'è anche un metodo più veloce per calcolare la complessità dell'algoritmo.
Una volta calcolato il numero di esecuzione per ciascuna linea del codice

Posso calcolare il costo asintotico direttamente su ogni riga.

A questo punto posso considerare il valore più significativo ( più alto ) come rappresentativo della complessità dell'algoritmo.
Il risultato è sempre O(n2).
La scala della complessità
La complessità di un algoritmo può essere classificata in una delle seguenti categorie:
| O(n!) con k>0 | complessità fattoriale ( complessità massima ) |
| O(kn) con k>0 | complessità esponenziale |
| O(nk) con k>0 | complessità polinomiale |
| O(n3) | complessità cubica |
| O(n2) | complessità quadratica ( complessità media ) |
| O(n·log n) | complessità pseudolineare |
| O(n) | complessità lineare ( complessità minima ) |
| O(log n) | complessità logaritmica |
| O(k) | complessità costante - es. O(1) |
Nota. La funzione O() è detta big-o. Si tratta di una notazione introdotta da Bachmann nel XIX secolo per indicare un ordine di grandezza della crescita di una funzione f(x) al crescere della variabile indipendente x, trascurando gli aspetti marginali. Nell'applicazione informatica la f(x) è il tempo di esecuzione o lo spazio di memoria di un programma, la variabile x è la quantità dei dati che il programma deve elaborare.
Per rendere più chiaro il concetto, in questo grafico mostro come cambia il tempo di esecuzione (t) dell'algoritmo all'aumentare del numero dei dati (n) nelle varie complessità.
Per elaborare n=4 dati, un algoritmo lineare impiega un secondo (t=1) mentre un algoritmo a complessità polinomiale ben 12 secondi.
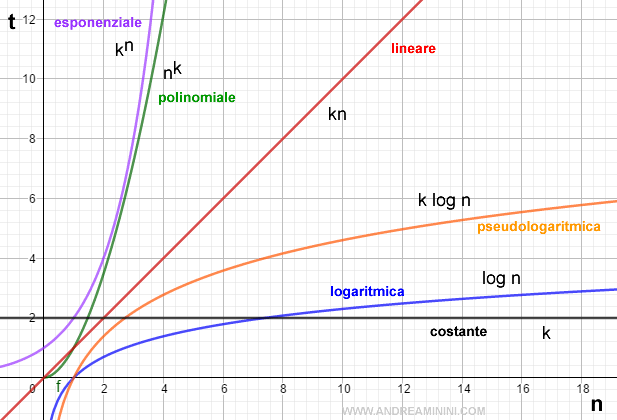
Nelle complessità superiori a quella lineare, la complessità cresce più rapidamente al crescere dei dati.
In alcuni casi, la ricerca della soluzione di un problema potrebbe richiedere anche anni di elaborazione.
Nota. Nel caso della complessità costante T(n)=O(k), il tempo di esecuzione non dipende dalla dimensione n dei dati di ingresso. Ad esempio T(n)=O(1). Per qualsiasi quantità di dati di ingresso (n), la complessità temporale dell'algoritmo è sempre la stessa O(k) dove k è una costante.
Problemi P e NP
A seconda della complessità dell'algoritmo esistono due classi di problemi: P e NP.
La classe P
La classe P comprende tutti i problemi trattabili, ossia risolvibili da un algoritmo in tempo ragionevole.
Appartengono alla classe P gli algoritmi di complessità polinomiale da cui prende il nome la classe.
La classe NP
La classe NP include i problemi risolvibili da algoritmi non deterministici, la cui soluzione può essere verificata con un algoritmo polinomiale.
Un algoritmo della classe NP ( Non Polinomiale ) elenca tutte le possibili soluzioni del problema usando un algoritmo di complessità non polinomiale ( ad esempio esponenziale ).
Poi verificano ogni singola soluzione con un algoritmo polinomiale.
Esempio. Un algoritmo deve trovare un cammino che passa per tutti i vertici di un grafo. Un primo algoritmo esponenziale elenca tutti i possibili cicli del grafo. Un secondo algoritmo polinomiale verifica se il ciclo è hamiltoniano.
La relazione tra P e NP
La classe dei problemi P è un sottoinsieme della classe NP.
P⊆NP
Non si può però affermare con certezza l'esistenza della relazione P=NP e di conseguenza nemmeno di P⊂NP.
E' uno dei problemi dell'informatica teorica ancora aperti su cui si discute.
Nota. E' comunque opinione diffusa che P≠NP.
E così via.
