La catena di Markov

La catena di Markov è una rappresentazione grafica delle relazioni di dipendenza tra le variabili di un sistema. E' anche detta processo di Markov o processo markoviano.

A cosa servono le catene di Markov? Le catene di Markov sono utili per analizzare le relazioni di causa ed effetto tra le variabili e trovare le soluzioni di un problema.

Si chiama così perché è stata usata per la prima volta dal matematico russo Andrei Markov.

Un esempio di catena di Markov

La catena di Markov viene rappresentata come una rete di nodi e archi ( o reye bayesiana ).

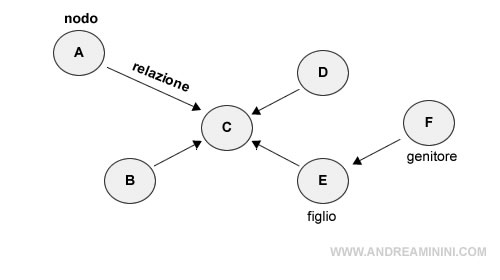
I nodi identificano le variabili del sistema.

Gli archi, invece, rappresentano la relazione tra due o più variabili.

Ogni arco è caratterizato da una freccia orientata verso la variabile dipendente.

Esempio. Il nodo F è la variabile indipendente ( nodo genitore ) che determina il valore del nodo E. Quest'ultima è la variabile dipendente ( nodo figlio ). A sua volta il nodo E è uno dei genitori del nodo C ( figlio ).

L'ipotesi di Markov

L'ipotesi di Markov è una ipotesi semplificatrice usata per analizzare i modelli dinamici, ossia quei sistemi che evolvono nel corso del tempo.

Secondo l'ipotesi di Markov si assume che ogni variabile di stato è determinata dallo stato precedente.

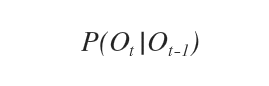
In altri termini, la variabile O nell'istante t è determinata dal valore della variabile O nell'istante t-1.

La lettera P indica che si tratta di un valore probabilistico ( probabilità condizionata ).

Si tratta di un modello di transizione abbastanza semplice, in cui il valore corrente delle variabili è determinato dalla loro storia passata.

Nota. Si parla di modello di transizione perché i valori degli stati precedenti sono osservabili in modo diretto. Se non fossero osservabili si parlerebbe, invece, di modello sensoriale.

I processi di Markov di primo, secondo e terzo grado

Le relazioni di Markov sono classificate in gradi ( o ordini ).

Ogni grado indica la relazione con lo stato precedente.

Alcuni esempi pratici di catene di Markov

Nel processo di Markov di primo grado la variabile è determinata dallo stato immediatamente precedente (t-1).

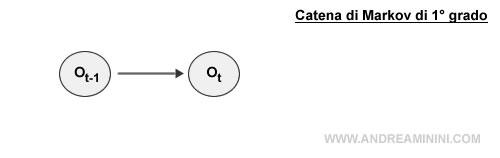
Nota. Nel processo di Markov di primo grado la previsione del futuro si basa esclusivamente sull'informazione del passato prossimo, lo stadio immediatamente precedente a quello corrente.

Nel processo di Markov di secondo grado, invece, la variabile nell'istante t è determinata dagli ultimi due stati ( t-1 , t-2 ).

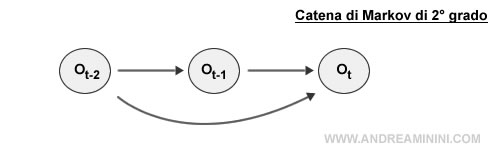
Nel processo di Markov di terzo grado, infine, la variabile nell'istante t è determinata dagli ultimi tre stati ( t-1, t-2, t-3 ).

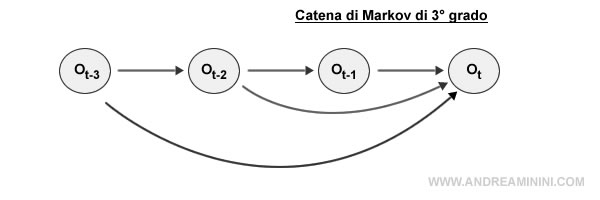
E così via.