L'algoritmo di valutazione delle informazioni aggiuntive
Prima di raccogliere un'informazione Ej e aggiungerla alla sua base di conoscenza KB ( Knowledge base ), l'agente razionale deve calcolare l'incremento dell'utilità dell'info aggiuntiva rispetto a tutte le altre.
Perché valutare le informazioni da aggiungere? La raccolta delle informazioni aggiuntive segue un ordine logico basato sull'utilità netta apportata dall'info. Vanno raccolte prima le informazioni più utili. Per farlo, l'agente deve ordinare l'utilità attesa EU di ogni informazione aggiuntiva Ej con j=1...n.
Come valutare informazione aggiuntiva
Non è sempre così semplice fare una valutazione ex-ante dell'informazione.
L'agente razionale non conosce con precisione l'utilità che un'informazione aggiuntiva può apportare alla sua conoscenza.
Pertanto, non si tratta di un processo deterministico con una relazione di causa-effetto in condizioni di certezza.
E' più che altro un processo probabilistico.
Un esempio pratico
Un'azione A potrebbe apportare un aumento di utilità pari a UA.
Non essendo un risultato sicuro, viene calcolata la distribuzione della probabilità intorno al valore medio UA.
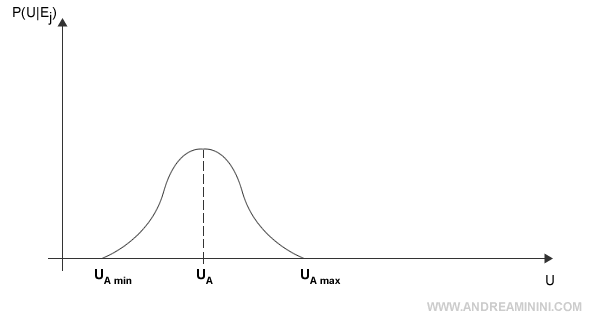
In questo caso la dispersione di probabilità P(U|Ej) è molto ampia, l'informazione aggiuntiva Ej è particolarmente utile perché consente di stabilire con maggiore precisione l'utilità attesa U'A dell'azione A.
Tuttavia, questo non vuol dire nulla perché l'agente non ha alternative.
L'informazione aggiuntiva non cambierebbe i suoi piani.
Esempio. L'agente deve percorrere la strada A ma non conosce la situazione del traffico stradale. Non ci sono alternative e la strada A è l'unica possibile. Inoltre, l'agente non ha fretta. L'informazione aggiuntiva ( il bollettino del traffico ) non cambia la sua decisione.
Se invece l'agente dovesse scegliere tra due azioni alternative A e B e l'azione B fosse decisamente più utile di A, la situazione sarebbe diversa.
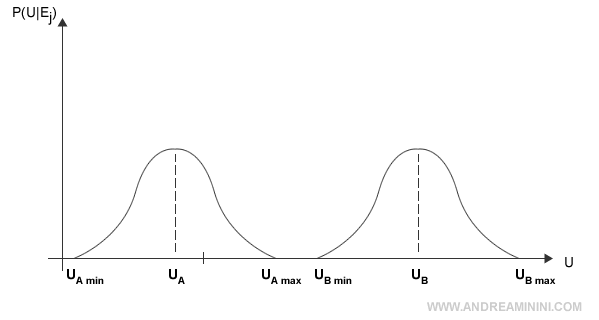
Tuttavia, anche in questo caso non c'è bisogno di alcuna informazione aggiuntiva (Ej).
Le due distribuzioni di probabilità non si toccano nemmeno, il peggiore risultato ottenibile dall'azione B (UBmin) sarebbe comunque meglio del migliore risultato ottenibile dall'azione A (UAmax).
L'informazione aggiuntiva non cambierebbe la decisione dell'agente.
Esempio. L'agente deve scegliere tra due strade A e B. La strada B ( es. autostrada ) è meno lunga, più larga e rapida della strada A ( es. strada statale ). E' evidente che la scelta razionale sia B. Non c'è bisogno di alcuna informazione aggiuntiva Ej. L'agente non conosce lo stato o il traffico della strada B ma non ha comunque alternative altrettanto valide tra cui scegliere.
Viceversa, se la distribuzione di probabilità fosse quasi sovrapposta, l'informazione aggiuntiva Ej avrebbe una grande importanza.
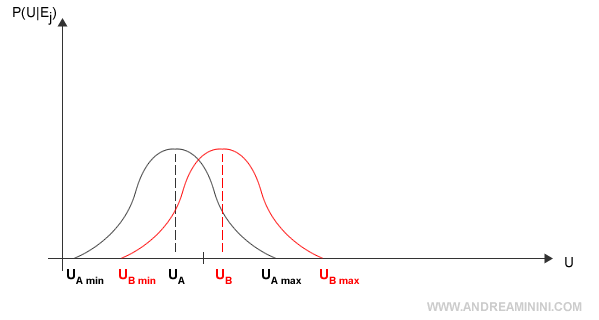
In questo caso l'informazione aggiuntiva consentirebbe all'agente di sapere con maggiore precisione l'utilità U'A e U'B effettiva e ridurre il rischio di fare una scelta sbagliata.
L'informazione aggiuntiva può modificare il piano di azione dell'agente.
Esempio. L'agente deve scegliere tra due strade A e B della stessa lunghezza. Tuttavia, una delle due strade potrebbe essere chiusa a causa del maltempo. L'informazione aggiuntiva Ej è molto utile.
D'altra parte, se la dispersione delle probabilità fosse molto piccola e le utilità molto vicine tra loro, l'informazione Ej non sarebbe poi così utile. Scegliere l'una o l'altra non cambia molto.
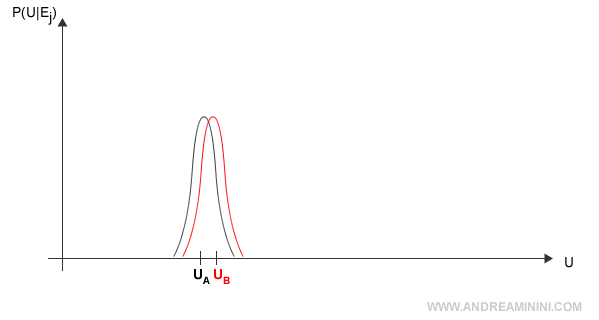
In questo caso è più razionale ed economica una scelta casuale ( random ).
Esempio. L'agente deve scegliere tra due strade A e B della stessa lunghezza. Da diverse settimane non piove, è quindi improbabile che ci siano state frane. Il rischio è molto basso.
