La predizione
La predizione è un modello previsionale che calcola la probabilità P di uno stato futuro Xt+k utilizzando tutte le variabili di prova raccolte in passato O1:t.
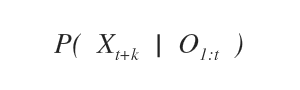
Si tratta di un modello di inferenza temporale.
A cosa serve la predizione? E' utile per capire quali saranno i probabili scenari del prossimo futuro.
Qual è la differenza tra filtraggio e predizione
Con il modello di monitoring ( filtraggio ) posso calcolare la probabilità di pioggia odierna e di domani in base:
- all'ultima prova raccolta, se vedo arrivare in ufficio una persona con l'ombrello oppure no ( modello sensoriale )
- ai giorni precedenti di pioggia ( modello di transizione )
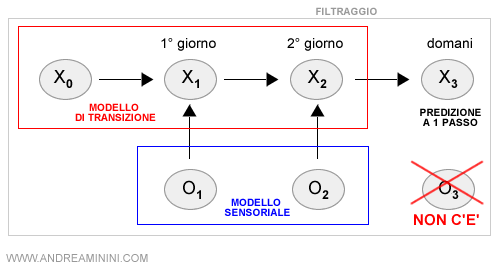
Nota. La formula filtraggio contiene già una predizione a un passo t+1 (ossia O3). Nella formula è la seconda probabilità condizionata P(Xt+1|O1:t).

Nel caso della predizione, invece, devo stimare se dopodomani pioverà oppure no.
In questo caso non ho a disposizione nessuna variabile di prova ( ombrello ) perché la persona arriverà dopodomani in ufficio e non posso già sapere se porterà con sé l'ombrello oppure no.
Non posso aggiungere nuove variabili di prova (O).
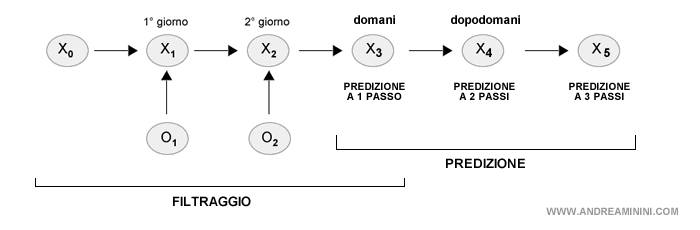
Pertanto, per fare una predizione non posso usare il modello sensoriale ( variabili di prova ). Posso basarmi esclusivamente sul modello di transizione.
La formula della predizione
La formula generale della predizione per k passi in avanti è la seguente:
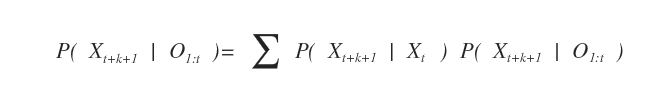
Un esempio pratico di calcolo della predizione
In questo esempio riprendo la situazione calcolata nel filtraggio fino al secondo giorno ( vedi esempio di filtraggio ) .
Secondo il modello di transizione, la probabilità di pioggia è del 70% se ha piovuto il giorno precedente.
La probabilità scende al 30% se il giorno precedente non ha piovuto.

In base alle osservazioni passate le probabilità di pioggia di oggi sono pari al 88%.
A questo punto passo a calcolare la predizione a un passo in avanti ( k=1 ), ossia la probabilità di pioggia domani.
Non avendo variabili di prova osservate, la probabilità che un collega si presenti in ufficio domani con un ombrello è del 50%.

In base alla calcolo della predizione, domani la probabilità di pioggia è del 66%.
Una volta ottenuta la predizione sul giorno successivo, posso calcolare la predizione a due passi in avanti ( k=2 ) per dopodomani.
La modalità di calcolo è sempre la stessa.

Dopodomani la probabilità di pioggia è pari al 56%. E così via.
Quali sono gli svantaggi della predizione
La predizione è utile per calcolare i probabili scenari futuri a breve o brevissimo termine, ossia per pochi passi in avanti.
Quando i passi in avanti sono molti, la predizione perde di efficacia perché le probabilità convergono verso un punto fisso.
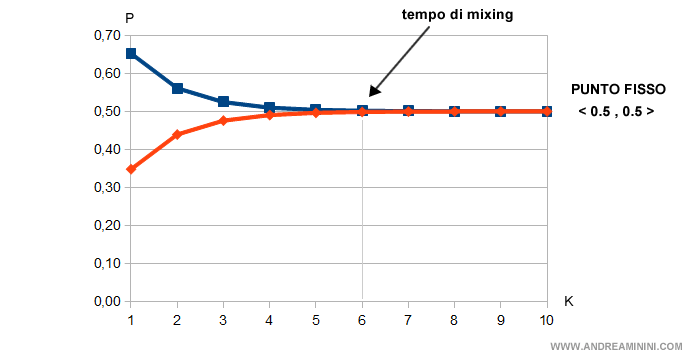
Perché la probabilità futura converge al 50?
Quanto più si va avanti, tanto più aumenta l'incertezza previsionale del modello di transizione.
Si arriva a un punto in cui non si può più affermare nessuna probabilità sull'evento.
In condizioni di ignoranza si stabilisce una probabilità del 50%.
Nota. Nel caso delle variabili booleane ( vero o falso ) il punto fisso è il 50%. Può comunque trattarsi di una percentuale differente. Ad esempio, in una variabile a tre stati possibili è il 33%. E così via.
Quanto si raggiunge il punto fisso?
Alcuni modelli di transizione raggiungono prima il punto fisso, mentre altri dopo.
Il tempo necessario per raggiungere la distribuzione stazionaria ( punto fisso ) è detto tempo di mixing.
Nota. Nell'esempio precedente il mixing si raggiunge con la predizione a sei passi in avanti ( k=6 ).
