La regolarizzazione
La regolarizzazione ( o smoothing ) è un modello di inferenza temporale usato per analizzare uno stato X in un istante passato K, considerando tutte le prove raccolte fino a oggi O1:T.
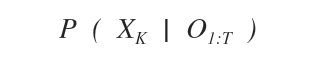
A cosa serve la regolarizzazione? Lo scopo della regolarizzazione è la ricostruzione degli eventi accaduti in passato, in modo logico e attendibile, utilizzando tutte le informazioni a propria disposizione. Anche le informazioni successive all'evento storico.
Qual è la differenza tra filtraggio, predizione e regolarizzazione?
Nella regolarizzazione si ricostruisce una situazione passata XK prendendo in considerazione tutte le variabili di prova a disposizione da O1 a OT.
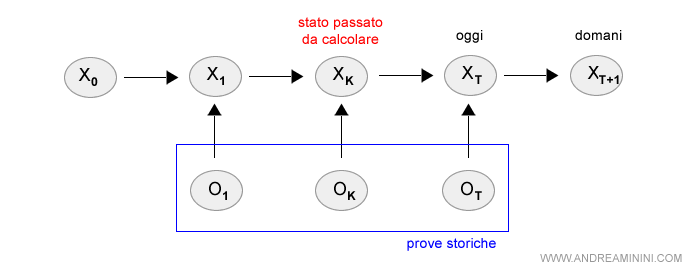
Nel filtraggio, invece, il modello ricostruisce la situazione corrente XT e predice lo stato futuro a un passo in avanti XT+1 ( futuro prossimo ) a partire dallo stato iniziale zero X0, considerando tutte le prove da O1 a OT.
Nella predizione, infine, si stima l'evoluzione futura della situazione con N passi in avanti da XT+1 a XT+N ( futuro remoto ) sulla base delle prove raccolte fino a oggi da O1 a OT.
La formula di smoothing
La formula di smoothing ( regolarizzazione ) è la seguente:
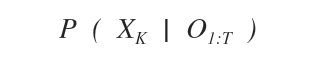
A questo punto suddivido le variabili di prova O in due gruppi.
Nel primo gruppo considero le prove dall'istante zero a K, mentre nel secondo gruppo quelle dall'istante K+1 a T.
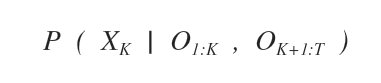
Ora applico la regola di Bayes normalizzata.
Nota. Secondo la regola generale di Bayes una probabilità condizionata P(A|B) può essere normalizzata e scomposta in α P(B|A)P(A). Dove alfa (α) è un fattore moltiplicativo che consente di avere la somma delle probabilità pari a 1.
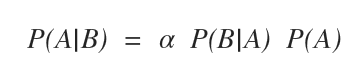
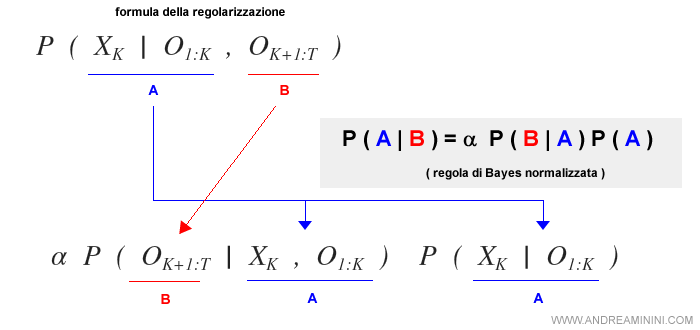
Nella prima componente posso eliminare O1:K per la regola della prova di Markov.
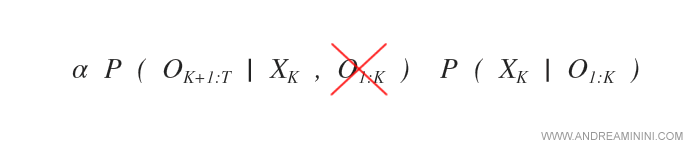
Nota. Secondo la proprietà di Markov della prova per calcolare la probabilità di una variabile casuale basta considerare l'ultima osservazione corrente. Le osservazioni passate O1:K possono essere eliminate.

A questo punto la formula della regolarizzazione può essere affrontata separatamente nelle sue due componenti.
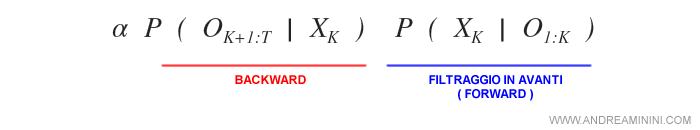
La prima componente è un processo ricorsivo all'indietro a partire da T fino a K+1.
La seconda è un filtraggio in avanti ( forward ) a partire da zero fino a K. Questa componente si calcola utilizzando il modello di transizione del filtraggio.
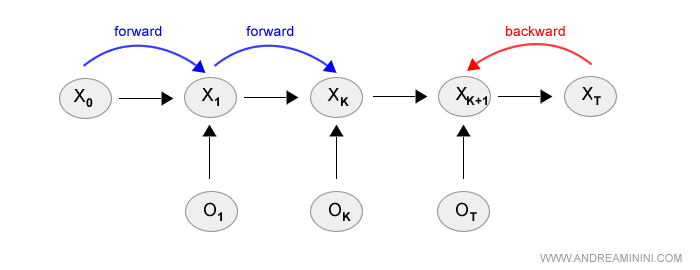
La formula della componente backward si ottiene nel seguente modo:
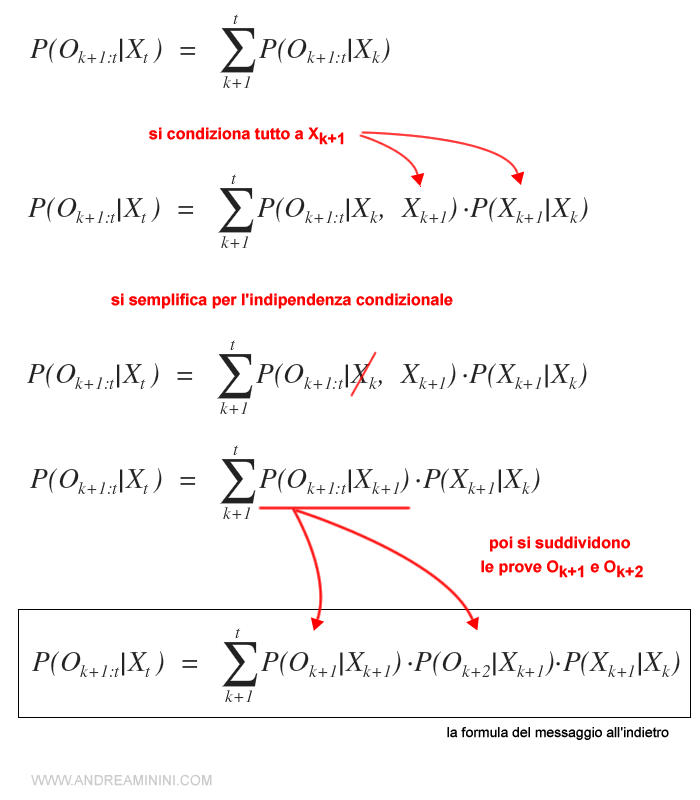
Nota. La formula della componente in avanti ( forward ) è sempre la stessa usata per costruire un modello di filtraggio ed è la seguente.
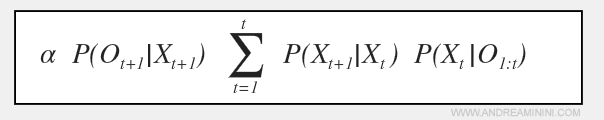
Un esempio pratico
Riprendo l'esempio del deposito sotterraneo dove non posso vedere se fuori piove o no.
L'unica prova a mia disposizione è vedere se i colleghi che arrivano in ufficio hanno l'ombrello oppure no.
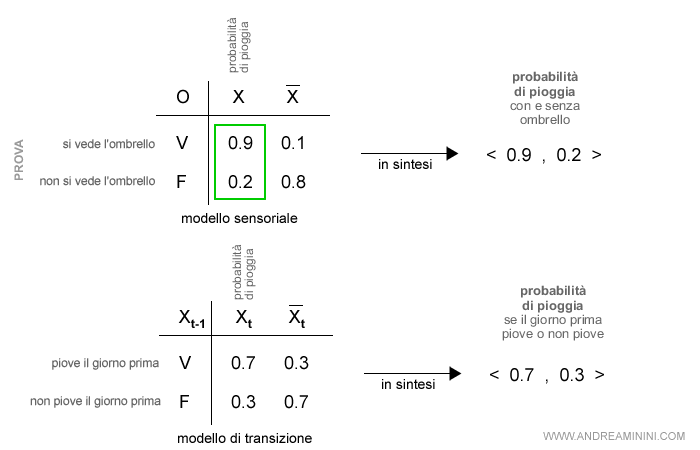
Le condizioni del modello sensoriale e di transizioni sono le seguenti:
Oggi è il secondo giorno (K=2) e sono più di due giorni che non esco.
A differenza del filtraggio, in questo caso non c'è una predizione perché conosco tutte le prove a mia disposizione.
So già che sia il primo giorno che il secondo giorno i colleghi arrivano in ufficio con l'ombrello (O1 e O2 sono veri).
Ovviamente non so se fuori piove oppure no perché non sono ancora uscito.
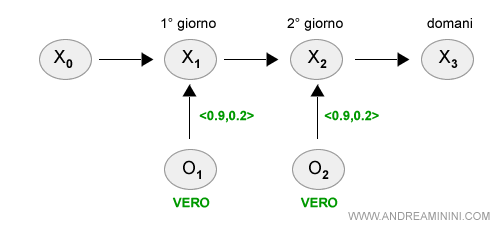
A questo punto mi chiedo quale è la probabilità di pioggia nel primo giorno (K=1).
Per ottenere questa risposta calcolo la regolarizzazione della probabilità di pioggia in K=1.
La formula della regolarizzazione è la seguente:
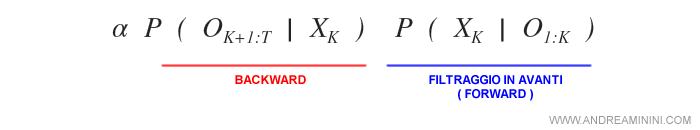
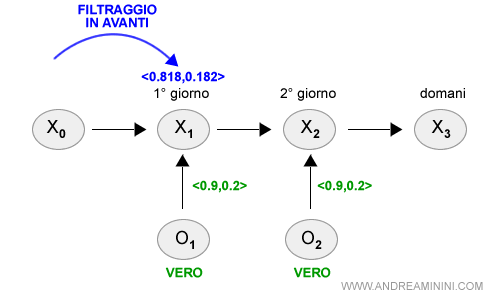
Come prima cosa calcolo la probabilità di pioggia nel primo giorno con il filtraggio in avanti.
Nota. Non conosco se nel giorno X0 stesse piovendo oppure no. Pertanto, nel modello di transizione considero il 50% di probabilità di pioggia nel giorno X0. Nel modello sensoriale, invece, uso la probabilità <0.9, 0.2> perché i colleghi hanno portato l'ombrello in ufficio.
Ho già calcolato la probabilità di pioggia nel primo giorno nell'esempio del filtraggio. Evito di riscrivere i calcoli.
Nel primo giorno la probabilità di pioggia è <0.818 , 0.182> secondo il filtraggio in avanti.
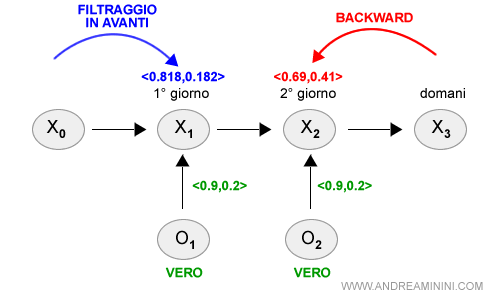
Ora posso calcolare la probabilità di pioggia nel giorno successivo (K=2) considerando la prova del giorno successivo (K=2).
So già che anche nel secondo giorno è comparso l'ombrello (O2=vero). Pertanto, la probabilità di pioggia del modello sensoriale è <0.9,0.2>.
Nel secondo giorno (K=2) la probabilità di pioggia è <0.69 , 0.41> secondo la propagazione all'indietro ( backward ) rispettivamente se i colleghi si presentano con o senza ombrello.

Ho così ottenuto entrambe le componenti della formula della regolarizzazione.
A questo punto posso calcolare la stima regolarizzata della probabilità di pioggia in K=1.

Secondo la regolarizzazione nel giorno K la probabilità di pioggia è pari all'88% ( <0.88 , 0.12> ).
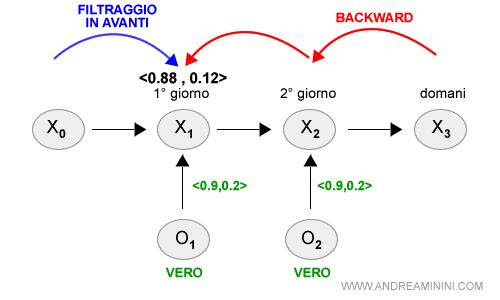
Nota. La probabilità di pioggia in K=1 secondo il filtraggio era 0.818 (81,8%) mentre quella calcolata con la regolarizzazione è più alta (88%) perché considera anche le prove del giorno successivo (K=2). Poiché vedo un ombrello anche nel giorno successivo (K=2) la probabilità di pioggia nel giorno successivo è alta e influenza anche la probabilità regolarizzata nel giorno K=1 perché la probabilità di pioggia è maggiore se piove anche nel giorno più vicino.
