Il modello di Markov nascosto
Il modello di Markov nascosto è un modello temporale probabilistico in cui lo stato del mondo si basa su una singola variabile casuale discreta ( cd variabile di stato ).
Il modello nascosto di Markov è anche conosciuto con la sigla HMM ( Hidden Markov Model ).
Un semplice esempio di Hidden Markov Model
Un esempio classico di HMM è quello in cui cerchiamo di capire se fuori fa caldo osservando l'abbigliamento dei passanti.
La temperatura esterna ( T ) è la variabile nascosta che misura lo stato del mondo ( giornata calda o no ).
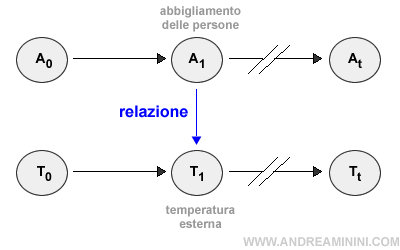
L'abbigliamento delle persone ( A ) è, invece, la variabile di prova che osserviamo direttamente e ci aiuta a calcolare la probabilità di pioggia all'esterno.
La variabile nascosta T è determinata dal:
- Modello di transizione. E' la relazione che collega la variabile Tt allo stato del mondo precedente Tt-1.
Nota. La variabile nascosta T è una variabile casuale. Può assumere valori decimali da 0 a 1.0 per indicare la probabilità che la giornata sia calda ( es. 75% calda ).
- Modello sensoriale. E' la relazione che lega la variabile nascosta Tt ( giornata calda o no ) all'osservazione della variabile di prova At ( abbigliamento leggero dei passanti o no ).
Nota. La variabile di prova è una variabile booleana perché può assumere soltanto il valore vero o falso. Se vediamo i passanti con un abbigliamento leggero la variabile è vera ( A=1 ) altrimenti è falsa ( A=0 ).
Il modello di Markov nascosto a matrice
Il modello di Markov nascosto può comunque essere esteso anche a più stati, se si considera la variabile di stato come una tupla di valori, un vettore o una matrice.

Nota. Nel modello la variabile di stato è sempre una ma comprende al suo interno una combinazioni di N stati del mondo. Ad esempio, invece di avere un solo stato ( caldo ) se ne possono considerare diversi ( afa, caldo, temperato, fresco, freddo ).
Ogni elemento della matrice indica la probabilità di transizione P(Tt|Tt-1) dallo stato I allo stato J.

Esempio. Oggi (t) la giornata ha la probabilità condizionata di essere calda pari a 0.70 (70%) se anche ieri (t-1) la giornata è stata calda e a 0.30 (30%) se invece ieri è stata una giornata non calda ( fredda ). Il modello di transizione a matrice può essere scritto nel seguente modo:

Allo stesso modo anche il modello sensoriale P(At|Tt) può essere rappresentato con una matrice.
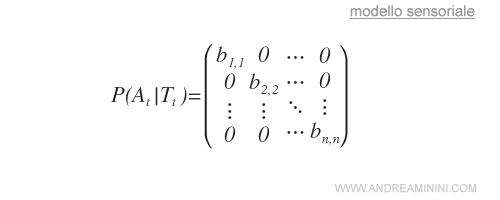
Esempio. La giornata calda ha una probabilità condizionata di verificarsi pari a 0.9 se osserviamo i passanti con un abbigliamento leggero e di 0.2 se hanno un abbigliamento pesante. La matrice sensoriale sarebbe scritta nel seguente modo:

