Come visualizzare le formule matematiche in html

Per mostrare i simboli matematici in un sito web utilizzo la libreria opensource MathJax. E' sviluppata in javascript e mi permette di utilizzare le sintassi di MathML, TeX, LaTeX e ASCIImath sul sito web.

A cosa serve MathJax? Questa libreria interpreta il codice testuale della pagina, lo trasforma nella sintassi tipica delle formule matematiche e lo visualizza sul browser dell'utente.

Come usare MathJax su un sito

E' molto facile da utilizzare. Basta inserire nella sezione head del documento html lo script che richiama la libreria Mathjax.

<script src='https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.5/MathJax.js?config=TeX-MML-AM_CHTML' async></script>

A questo punto nella sezione <body> della pagina web posso digitare le formule matematiche nella sintassi Math direttamente nel codice HTML.

Il codice delle formule matematiche va inserito tra due delimitatori di apertura e chiusura $$ ( doppio dollaro ).

$$ sintassi $$

Tutto ciò che è dentro questi delimitatori, viene elaborato dalla libreria MathJax e mostrato in forma grafica.

Un esempio pratico

Questo documento html richiama la libreria MathJax.

  1. <!DOCTYPE html>
  2. <html>
  3. <head>
  4. <title>MathJax TeX Test Page</title>
  5. <script src='https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.5/MathJax.js?config=TeX-MML-AM_CHTML' async></script>
  6. </head>
  7. <body>
  8. X_1 <br>
  9. $$ X_1 $$
  10. </body>
  11. </html>

Quando il browser apre questa pagina web, richiama la libreria MathJax ed elabora il testo.

La pagina web appare sul browser in questo modo.

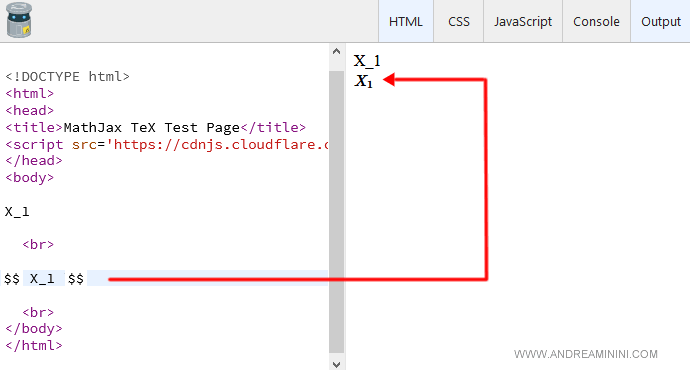
un esempio pratico

Come si può vedere X_1 è stato elaborato in modo diverso dentro i delimitatori \( \).

Questo è soltanto un esempio banale per spiegare come funziona MathJax.

Seguendo la sintassi del linguaggio di MathJax posso creare anche formule matematiche molto più complesse.

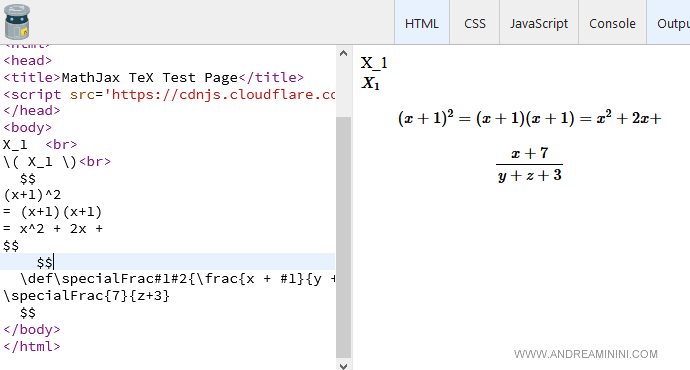
un altro esempio pratico di utilizzo

Lista dei codici LatTeX in MathJax

Per imparare a conoscere tutti i simboli di MathJax consulto questo elenco online. E' abbastanza completo.

codice risultato descrizione
$$ x_n $$ $$ x_n $$  
$$ x^n $$ $$ x^n $$ potenza
$$ x^{i_2} $$ $$ x^{i_2} $$  
$$ x^{i^2} $$ $$ x^{i^2} $$  
$$ {x^i}^2 $$ $$ {x^i}^2 $$  
$$ ^ax^b $$ $$ ^ax^b $$  
$$ \require{cancel} \cancel{x} $$ $$ \require{cancel} \cancel{x} $$  
$$ \require{cancel} \cancel{testo} $$ $$ \require{cancel} \cancel{testo} $$  
$$ \not{x} $$ $$ \not{x} $$  
$$ \rlap{\backslash} x $$ $$ \rlap{\backslash} x $$  
$$ \sum_{n=1}^\infty $$ $$ \sum_{n=1}^\infty $$  
$$ \overbrace{x+\cdots+x} $$ $$ \overbrace{x+\cdots+x} $$  
$$ \underbrace{x+\cdots+x} $$ $$ \underbrace{x+\cdots+x} $$  
$$ \underset{bottom}{base} $$ $$ \underset{bottom}{base} $$  
$$ \stackrel{top}{bottom} $$ $$ \stackrel{top}{bottom} $$  
$$ ^{n\text{ times}} $$ $$ ^{n\text{ times}} $$  
$$ \frac{x+1}{x-1} $$ $$ \frac{x+1}{x-1} $$ frazione
$$ \binom n k $$ $$ \binom n k $$ binomio
$$ \left(\frac{x}{y}\right) $$ $$ \left(\frac{x}{y}\right) $$  
$$ \left\{\frac{x}{y}\right\} $$ $$ \left\{\frac{x}{y}\right\} $$  
$$ \left[\frac{x}{y}\right] $$ $$ \left[\frac{x}{y}\right] $$  
$$ \{1,2,3\} $$ $$ \{1,2,3\} $$  
$$ \sqrt[89]{x+4} $$ $$ \sqrt[n]{x+y} $$ radice
$$ \lim_{x\to 5}{x+y} $$ $$ \lim_{x\to 5}{x+y} $$ limite
$$ \log_{a}{b} $$ $$ \log_{a}{b} $$ logaritmo
$$ \int_{a}^{b}{x dx} $$ $$ \int_{a}^{b}{x dx} $$ integrale definito
$$ \int{x dx} $$ $$ \int{x dx} $$ integrale indefinito
$$ \iint{f \ dx \ dy} $$ $$ \iint{f \ dx \ dy} $$ integrale doppio
$$ \iiint{f \ dx \ dy \ dz} $$ $$ \iiint{f \ dx \ dy \ dz} $$ integrale triplo
$$ \sum_{i=1}^{a}{b^{i}} $$ $$ \sum_{i=1}^{a}{b^{i}} $$ sommatoria
$$ \prod_{i=1}^{a}{b^{i}} $$ $$ \prod_{i=1}^{a}{b^{i}} $$ produttoria
$$ \overrightarrow{V} $$ $$ \overrightarrow{V} $$ vettore
$$ \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{matrix} $$ $$ \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{matrix} $$ matrice
$$ \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{pmatrix} $$ $$ \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{pmatrix} $$ matrice
$$ \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{bmatrix} $$ $$ \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{bmatrix} $$ matrice
$$ \begin{Bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{Bmatrix} $$ $$ \begin{Bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{Bmatrix} $$ matrice
$$ \begin{vmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{vmatrix} $$ $$ \begin{vmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{vmatrix} $$ matrice
$$ \begin{Vmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{Vmatrix} $$ $$ \begin{Vmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{Vmatrix} $$ matrice
$$ \begin{cases}y=x\\ y=x+1\end{cases} $$ $$ \begin{cases}y=x\\ y=x+1\end{cases} $$ sistema
$$ \begin{array}{c|c} x & y \\ \hline 0 & 0 \\ 1 & 1 \\ 2 & 2\\ 3 & 3 \end{array} $$ $$ \begin{array}{c|c} x & y \\ \hline 0 & 0 \\ 1 & 1 \\ 2 & 2\\ 3 & 3 \end{array} $$ tabella semplice
$$ \begin{array}{c|lcr} n & \text{a} & \text{b} & \text{c} \\ \hline 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \end{array} $$ $$ \begin{array}{c|lcr} n & \text{a} & \text{b} & \text{c} \\ \hline 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \end{array} $$ array / tabella
$$ \begin{array}{cr|c} p & q & p∧q \\ \hline 0 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 1 & 1 \end{array} $$ $$ \begin{array}{cr|c} p & q & p∧q \\ \hline 0 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 1 & 1 \end{array} $$ tabella
$$ f(n) = \begin{cases} n/2, & \text{if $n$ is even} \\ 3n+1, & \text{if $n$ is odd} \end{cases} $$ $$ f(n) = \begin{cases} n/2, & \text{if $n$ is even} \\ 3n+1, & \text{if $n$ is odd} \end{cases} $$  
$$ \left. \begin{array}{l} \text{if $n$ is even:}&n/2\\ \text{if $n$ is odd:}&3n+1 \end{array} \right\} =f(n) $$ $$ \left. \begin{array}{l} \text{if $n$ is even:}&n/2\\ \text{if $n$ is odd:}&3n+1 \end{array} \right\} =f(n) $$  
$$ \boxed{testo} $$ \boxed{testo} $$  
$$ \left| testo \right|   $$ \left| \frac{1}{2} \right| $$ parentesi grande
$$ \right)testo \right)
 $$ \left( \frac{1}{2} \right) $$ parentesi grande
$$ \small testo $$ \small testo $$ testo; piccolo
$$ \tiny testo $$ \tiny testo $$ testo; piccolo
$$ \textstyle testo $$ \textstyle testo $$ testo più piccolo
$$ \scriptstyle testo $$ \scriptstyle testo $$ testo ancora più piccolo
$$ \scriptscriptstyle{testo} $$ \scriptscriptstyle testo $$ testo ancora più piccolo
\mathbf{x} $$ \mathbf{A+B} $$ formule in grassetto
\boldsymbol{123} $$ \boldsymbol{123} $$ simboli in grassetto
\textbf{testo in grassetto} $$ \textbf{testo in grassetto} $$ testo in grassetto

Colori

$$ {\color{red} x} + {\color{blue} y} $$ $$ {\color{red} x} + {\color{blue} y} $$

La tabella dei simboli matematici

codice simbolo descrizione
\\ $$ a\\b $$ new line ( ritorno a capo su una nuova linea )
$$ \forall $$ \forall $$ per ogni
$$ \in $$ $$ \in $$  
$$ \notin $$ $$ \notin $$  
$$ \ni $$ $$ \ni $$  
$$ \ne $$ $$ \ne $$  
$$ \exists $$ $$ \exists $$  
$$ \cong $$ $$ \cong $$ isomorfismo, approssimativamente uguale
$$ \partial $$ $$ \partial $$ derivate parziali
$$ \nabla $$ $$ \nabla $$ Nabla
$$ \nexists $$ $$ \nexists $$  
$$ \nleq $$ $$ \nleq $$  
$$ \Re $$ $$ \Re $$  
$$ + $$ $$ + $$  
$$ \infty $$ $$ \infty $$  
$$ - $$ $$ - $$  
$$ \% $$ $$ \% $$  
$$ \times $$ $$ \times $$  
$$ \circ $$ $$ \circ $$  
$$ \cdot $$ $$ \cdot $$  
$$ ^{\circ} $$ $$ ^{\circ} $$  
$$ : $$ $$ : $$  
$$ \vee $$ $$ \vee $$  
$$ / $$ $$ / $$  
$$ \wedge $$ $$ \wedge $$  
$$ \pm $$ $$ \pm $$  
$$ \cup $$ $$ \cup $$  
$$ \bigcup $$ $$ \bigcup $$  
$$ \mp $$ $$ \mp $$  
$$ \cap $$ $$ \cap $$  
$$ \bigcap $$ $$ \bigcap $$  
$$ \sim $$ $$ \sim $$  
$$ \subset $$ $$ \subset $$  
$$ \simeq $$ $$ \simeq $$  
$$ \subseteq $$ $$ \subseteq $$  
$$ \equiv $$ $$ \equiv $$ Equivalenza
$$ \doteq $$ $$ \doteq $$ Uguale per definizione.
$$ \supset $$ $$ \supset $$  
$$ \approx $$ $$ \approx $$  
$$ \approxeq $$ $$ \approxeq $$  
$$ \supseteq $$ $$ \supseteq $$  
$$ < $$ $$ < $$  
$$ \oplus $$ $$ \oplus $$ somma diretta
$$ \leq $$ $$ \leq $$  
$$ \uplus $$ $$ \uplus $$  
$$ > $$ $$ > $$  
$$ \ominus $$ $$ \ominus $$  
$$ \geq $$ $$ \geq $$  
$$ \otimes $$ $$ \otimes $$  
$$ \succ $$ $$ \succ $$  
$$ \prec $$ $$ \prec $$  
$$ \succeq $$ $$ \succeq $$  
$$ \preceq $$ $$ \preceq $$  
$$ \dots $$ $$ \dots $$  
$$ \diamond $$ $$ \diamond $$  
$$ \vdots $$ $$ \vdots $$  
$$ \bigtriangleup $$ $$ \bigtriangleup $$ determinante
$$ \ddots $$ $$ \ddots $$  
$$ \bigtriangledown $$ $$ \bigtriangledown $$  
$$ \nabla $$ $$ \nabla $$  
$$ \clubsuit $$ $$ \clubsuit $$  
$$ \emptyset $$ $$ \emptyset $$  
$$ \diamondsuit $$ $$ \diamondsuit $$  
$$ \heartsuit $$ $$ \heartsuit $$  
$$ \Re $$ $$ \Re $$  
$$ \perp $$ $$ \perp $$  
$$ \Im $$ $$ \Im $$  
$$ \parallel $$ $$ \parallel $$  
$$ \ell $$ $$ \ell $$  
$$ \{ \} $$ $$ \{ \} $$  

Le frecce

codice simbolo
$$ \to $$ $$ \to $$
$$ \leftarrow $$ $$ \leftarrow $$
$$ \Leftarrow $$ $$ \Leftarrow $$
$$ \rightarrow $$ $$ \rightarrow $$
$$ \Rightarrow $$ $$ \Rightarrow $$
$$ \longleftarrow $$ $$ \longleftarrow $$
$$ \Longleftarrow $$ $$ \Longleftarrow $$
$$ \longrightarrow $$ $$ \longrightarrow $$
$$ \Longrightarrow $$ $$ \Longrightarrow $$
$$ \uparrow $$ $$ \uparrow $$
$$ \Uparrow $$ $$ \Uparrow $$
$$ \downarrow $$ $$ \downarrow $$
$$ \Downarrow $$ $$ \Downarrow $$
$$ \leftrightarrow $$ $$ \leftrightarrow $$
$$ \Leftrightarrow $$ $$ \Leftrightarrow $$
$$ \longleftrightarrow $$ $$ \longleftrightarrow $$
$$ \Longleftrightarrow $$ $$ \Longleftrightarrow $$
$$ \updownarrow $$ $$ \updownarrow $$
$$ \Updownarrow $$ $$ \Updownarrow $$
$$ \mapsto $$ $$ \mapsto $$
$$ \longmapsto $$ $$ \longmapsto $$
$$ \nearrow $$ $$ \nearrow $$
$$ \searrow $$ $$ \searrow $$
$$ \swarrow $$ $$ \swarrow $$
$$ \nwarrow $$ $$ \nwarrow $$
$$ \hookleftarrow $$ $$ \hookleftarrow $$
$$ \hookrightarrow $$ $$ \hookrightarrow $$
$$ \leftharpoonup $$ $$ \leftharpoonup $$
$$ \rightharpoonup $$ $$ \rightharpoonup $$
$$ \leftharpoondown $$ $$ \leftharpoondown $$
$$ \rightharpoondown $$ $$ \rightharpoondown $$
$$ \leftrightharpoons $$ $$ \leftrightharpoons $$
$$ \rightleftharpoons $$ $$ \rightleftharpoons $$

Gli accenti

codice simbolo
$$ \hat{a} $$ $$ \hat{a} $$
$$ \dot{a} $$ $$ \dot{a} $$
$$ \acute{a} $$ $$ \acute{a} $$
$$ \ddot{a} $$ $$ \ddot{a} $$
$$ \grave{a} $$ $$ \grave{a} $$
$$ \check{a} $$ $$ \check{a} $$
$$ \bar{a} $$ $$ \bar{a} $$
$$ \vec{a} $$ $$ \vec{a} $$
$$ \tilde{a} $$ $$ \tilde{a} $$
$$ \breve{a} $$ $$ \breve{a} $$
$$ \widehat{abc} $$ $$ \widehat{abc} $$
$$ \widetilde{abc} $$ $$ \widetilde{abc} $$
$$ \overline{abc} $$ $$ \overline{abc} $$
$$ \overrightarrow{abc} $$ $$ \overrightarrow{abc} $$
$$ \overparen{abc} $$ $$ \overparen{abc} $$
$$ \underline{abc} $$ $$ \underline{abc} $$
$$ \overset{=}{x} $$ $$ \overset{=}{x} $$
$$ \underset{=}{x} $$ $$ \underset{=}{x} $$
$$ \overleftarrow{abc} $$ $$ \overleftarrow{abc} $$

Le lettere dell'alfabeto greco

codice simbolo descrizione
$$ \alpha $$ $$ \alpha $$  
$$ A $$ $$ A $$  
$$ \beta $$ $$ \beta $$  
$$ B $$ $$ B $$
$$ \gamma $$ $$ \gamma $$
$$ \Gamma $$ $$ \Gamma $$
$$ \delta $$ $$ \delta $$
$$ \Delta $$ $$ \Delta $$
$$ \epsilon $$ $$ \epsilon $$
$$ \varepsilon $$ $$ \varepsilon $$
$$ E $$ $$ E $$
$$ \zeta $$ $$ \zeta $$
$$ Z $$ $$ Z $$
$$ \eta $$ $$ \eta $$
$$ H $$ $$ H $$
$$ \theta $$ $$ \theta $$
$$ \vartheta $$ $$ \vartheta $$
$$ \Theta $$ $$ \Theta $$
$$ \iota $$ $$ \iota $$
$$ I $$ $$ I $$
$$ \kappa $$ $$ \kappa $$
$$ \varkappa $$ $$ \varkappa $$
$$ K $$ $$ K $$
$$ \lambda $$ $$ \lambda $$
$$ \Lambda $$ $$ \Lambda $$
$$ \mu $$ $$ \mu $$
$$ M $$ $$ M $$
$$ \ni $$ $$ \ni $$
$$ N $$ $$ N $$
$$ \xi $$ $$ \xi $$
$$ \Xi $$ $$ \Xi $$
$$ \omicron $$ $$ \omicron $$
$$ O $$ $$ O $$
$$ \pi $$ $$ \pi $$
$$ \varpi $$ $$ \varpi $$
$$ \Pi $$ $$ \Pi $$
$$ \rho $$ $$ \rho $$
$$ \varrho $$ $$ \varrho $$
$$ P $$ $$ P $$
$$ \sigma $$ $$ \sigma $$
$$ \varsigma $$ $$ \varsigma $$
$$ \Sigma $$ $$ \Sigma $$
$$ \tau $$ $$ \tau $$
$$ T $$ $$ T $$
$$ \upsilon $$ $$ \upsilon $$
$$ \Upsilon $$ $$ \Upsilon $$
$$ \phi $$ $$ \phi $$
$$ \varphi $$ $$ \varphi $$
$$ \Phi $$ $$ \Phi $$
$$ \chi $$ $$ \chi $$
$$ \Chi $$ $$ X $$
$$ \psi $$ $$ \psi $$
$$ \Psi $$ $$ \Psi $$
$$ \omega $$ $$ \omega $$
$$ \Omega $$ $$ \Omega $$

Per esercitarmi a usare la sintassi di MathJax, invece, utilizzo editor online.

E così via.

Per ulteriori info su MathJax, Math, LaTeX

https://www.mathjax.org
http://www.w3.org/Math/
http://www.latex-project.org/

 

 


 
Segnalami un errore, un refuso o un suggerimento per migliorare gli appunti

FacebookTwitterLinkedinLinkedin
knowledge base

Libri di approfondimento
  1. Il linguaggio Html