La regressione lineare semplice
La regressione lineare semplice è un modello statistico che permette di descrivere la relazione tra due variabili numeriche. È una delle tecniche più utilizzate in statistica descrittiva e inferenziale.
La regressione lineare semplice assume che la variabile dipendente $Y$ sia una funzione lineare della variabile indipendente $X$, più un termine di errore casuale.
In forma matematica:
$$ Y = a + bX + \varepsilon $$
Dove:
- $Y$ è la variabile risposta (dipendente)
- $X$ è la variabile esplicativa (indipendente)
- $a$ è l’intercetta
- $b$ è il coefficiente angolare
- $\varepsilon$ è il termine di errore aleatorio (non osservabile)
L'intercetta $a$ rappresenta il valore atteso di $Y$ quando $X = 0$. È l’ordinata all’origine della retta stimata.
Il coefficiente angolare $b$ indica quanto cambia in media la variabile $Y$ al variare di una unità della variabile $X$. È il tasso di variazione marginale.
Come trovare i parametri $ a $ e $ b $?
Inizialmente i valori $a$ e $b$ non sono noti. Vengono stimati a partire dai dati campionari tramite il metodo dei minimi quadrati.
Questo metodo cerca i coefficienti $\hat{a}$ e $\hat{b}$ in modo da minimizzare la somma dei quadrati degli scarti tra i valori osservati $y_i$ e quelli previsti dal modello $\hat{y}_i$:
$$ \text{SSE} = \sum_{i=1}^n (y_i - \hat{y}_i)^2 $$
Le formule per le stime sono:
$$
\hat{b} = \frac{ \sum (x_i - \bar{x})(y_i - \bar{y}) }{ \sum (x_i - \bar{x})^2 }
\quad ; \quad
\hat{a} = \bar{y} - \hat{b} \bar{x}
$$
Un esempio pratico
Voglio prevedere il punteggio in un test in funzione del numero di ore di studio settimanali.
Supponiamo che l’analisi dei dati fornisca:
$$ \hat{a} = 50 \quad ; \quad \hat{b} = 2 $$
L’equazione stimata diventa:
$$ \hat{y} = 50 + 2x $$
Se uno studente non studia ($x = 0$), ci si attende un punteggio medio di 50.
Ogni ora in più di studio settimanale comporta un incremento atteso di 2 punti nel test.
Nota. Questo modello non garantisce previsioni esatte, ma stima un valore medio atteso in base ai dati disponibili.
Esempio 2
Supponiamo di avere un piccolo campione con 5 osservazioni che registrano:
- $ X$: numero di ore di studio
- $Y$: livello di preparazione (misurato con un punteggio da 0 a 100)
I dati sono:
| i | xi (ore) | yi (preparazione) |
|---|---|---|
| 1 | 1 | 55 |
| 2 | 2 | 58 |
| 3 | 3 | 60 |
| 4 | 4 | 63 |
| 5 | 5 | 65 |
Voglio stimare la retta $\hat{y} = \hat{a} + \hat{b} x$ ma non conosco ancora il coefficiente e l'intercetta.
Per prima cosa calcolo le medie dei valori
$$ \bar{x} = \frac{1 + 2 + 3 + 4 + 5}{5} = \frac{15}{5} = 3 $$
$$ \bar{y} = \frac{55 + 58 + 60 + 63 + 65}{5} = \frac{301}{5} = 60.2 $$
Poi calcolo il numeratore per $\hat{b}$, cioè $\sum (x_i - \bar{x})(y_i - \bar{y})$:
| i | \(x_i - \bar{x}\) | \(y_i - \bar{y}\) | Prodotto |
|---|---|---|---|
| 1 | \(1 - 3 = -2\) | \(55 - 60.2 = -5.2\) | \((-2)(-5.2) = 10.4\) |
| 2 | \(2 - 3 = -1\) | \(58 - 60.2 = -2.2\) | \((-1)(-2.2) = 2.2\) |
| 3 | \(3 - 3 = 0\) | \(60 - 60.2 = -0.2\) | \(0 \cdot (-0.2) = 0\) |
| 4 | \(4 - 3 = +1\) | \(63 - 60.2 = 2.8\) | \(1 \cdot 2.8 = 2.8\) |
| 5 | \(5 - 3 = +2\) | \(65 - 60.2 = 4.8\) | \(2 \cdot 4.8 = 9.6\) |
La somma dei prodotto è:
$$ 10.4 + 2.2 + 0 + 2.8 + 9.6 = 25.0 $$
Quindi, calcolo il denominatore per $\hat{b}$, cioè $\sum (x_i - \bar{x})^2$:
| i | \(x_i - \bar{x}\) | Quadrato |
|---|---|---|
| 1 | \(-2\) | 4 |
| 2 | \(-1\) | 1 |
| 3 | 0 | 0 |
| 4 | \(+1\) | 1 |
| 5 | \(+2\) | 4 |
La somma dei quadrati è 10
$$ 4 + 1 + 0 + 1 + 4 = 10 $$
Questo mi permette di stimare il coefficiente angolare $\hat{b}$:
$$ \hat{b} = \frac{25.0}{10} = 2.5 $$
e l'intercetta $\hat{a}$:
$$ \hat{a} = \bar{y} - \hat{b}\,\bar{x} = 60.2 - 2.5 \cdot 3 = 60.2 - 7.5 = 52.7 $$
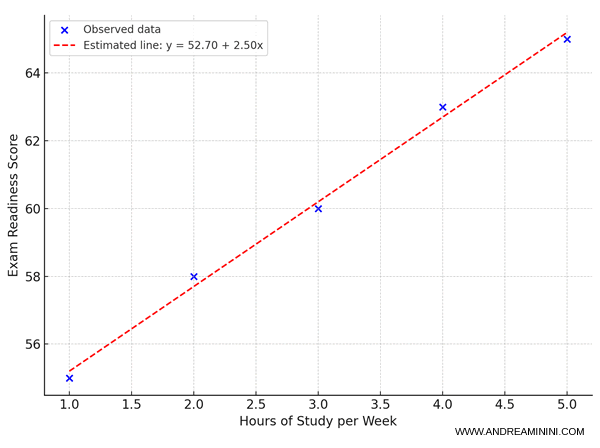
In base a questi calcoli la retta stimata è:
$$ \hat{y} = 52.7 + 2.5\,x $$
Questo significa che se una persona non studia ($x = 0$), la preparazione stimata è $\hat{y} = 52.7$.
Ogni ora aggiuntiva di studio settimanale è associata in media a un aumento di 2.5 punti nel punteggio di preparazione.
A questo punto, volendo posso calcolare i residui $e_i = y_i - \hat{y}_i$ per ogni osservazione, in modo da verificare la bontà dell’adattamento. Ad esempio:
- Per $i = 1$: $\hat{y}_1 = 52.7 + 2.5 \cdot 1 = 55.2$. Residuo $e_1 = 55 - 55.2 = -0.2$.
- Per $i = 2$: $\hat{y}_2 = 52.7 + 2.5 \cdot 2 = 57.7$. Residuo $e_2 = 58 - 57.7 = 0.3$.
- E così via.
Se i residui sono “piccoli”, il modello è accettabile, se invece mostrano tendenze sistematiche (ad esempio crescono con $x$), qualche ipotesi è probabilmente violata.
I limiti del modello
Il modello si basa su alcune ipotesi:
- Linearità: la relazione tra $X$ e $Y$ è rettilinea.
- Omogeneità della varianza: la dispersione degli errori è costante.
- Indipendenza degli errori.
- Normalità degli errori (per inferenza).
Quando una o più ipotesi vengono violate, il modello può diventare inadeguato.
Ad esempio, se la relazione tra $X$ e $Y$ è curva, una retta non riesce a descrivere correttamente l’andamento.
Quindi, l'utilizzo della regressione lineare semplice richiede sempre una verifica empirica dell’adeguatezza del modello. È il primo passo verso modelli statistici più sofisticati.
Pur essendo un modello elementare, la regressione lineare semplice pone le basi per affrontare strumenti statistici più complessi e apre la strada a una vasta gamma di sviluppi teorici e applicativi.
Quali sono le possibili estensioni del modello?
Uno dei principali sviluppi è la regressione multipla, che estende il modello lineare semplice a più di una variabile indipendente.
In questo caso, la variabile dipendente è spiegata non da una sola causa, ma da un insieme di fattori esplicativi.
Questo consente di descrivere fenomeni più realistici, nei quali le influenze sono molteplici e interconnesse.
Un’altra estensione importante riguarda i modelli non lineari.
Quando la relazione tra le variabili non segue un andamento rettilineo, la retta di regressione non è più adeguata. In questi casi si ricorre a funzioni più flessibili, come le parabole, le curve logaritmiche o esponenziali, che permettono di adattarsi meglio alla forma dei dati osservati.
La regressione semplice introduce anche concetti fondamentali come:
- Il coefficiente di determinazione $R^2$, che quantifica quanta parte della variabilità osservata in $Y$ è spiegata dal modello. Un valore vicino a 1 indica una buona capacità esplicativa, mentre un valore basso suggerisce che il modello non riesce a catturare la struttura del fenomeno.
- L’analisi dei residui, ossia l’esame delle differenze tra i valori osservati e quelli previsti dal modello. Questa analisi è essenziale per individuare anomalie, verificare la bontà dell’adattamento e controllare le ipotesi statistiche sottostanti.
In sintesi, pur nella sua semplicità, questo modello rappresenta un punto di partenza obbligato per chi vuole acquisire padronanza degli strumenti dell’analisi statistica.
