Come rappresentare il grafico di una funzione matematica in Python

In questo tutorial spiego come rappresentare il grafico di una o più funzioni matematiche in Python usando le librerie Matplotlib e Numpy.

Per prima cosa importo le librerie matplotlib e numpy.

import matplotlib.pyplot as plt
import numpy as np

Poi definisco le funzioni di alcune parabole e di una retta

def retta(x):
   return -x + 2

def parabola1(x):
   return x**2 - 3*x + 3

def parabola2(x):
   return -x**2 + x + 1

def parabola3(x):
   return 2*x**2 - 5*x + 4

Creo un range di valori per x

x = np.linspace(-2, 3, 400)

Calcolo i valori di y per ogni funzione

y_retta = retta(x)
y_parabola1 = parabola1(x)
y_parabola2 = parabola2(x)
y_parabola3 = parabola3(x)

Quindi, traccio le funzioni

plt.figure(figsize=(10, 6))
plt.plot(x, y_retta, label='y = -x + 2', color='red')
plt.plot(x, y_parabola1, label='y = x^2 - 3x + 3', color='blue')
plt.plot(x, y_parabola2, label='y = -x^2 + x + 1', color='green')
plt.plot(x, y_parabola3, label='y = 2x^2 - 5x + 4', color='purple')

Evidenzio il punto T(1, 1)

plt.scatter(1, 1, color='black', zorder=5)
plt.text(1, 1, ' T(1, 1)', verticalalignment='bottom', horizontalalignment='right')

Aggiungo la legenda e le etichette degli assi

plt.legend()

Visualizzo le variabili x e y sugli assi cartesiani

plt.xlabel('x')
plt.ylabel('y')

Aggiungo un titolo al grafico

plt.title('Fascio di parabole tangenti alla retta y = -x + 2 nel punto T(1, 1)')

Visualizzo una griglia

plt.grid(True)
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)

Infine visualizzo il grafico delle funzioni

plt.show()

Il risultato è una grafico che mostra il comportamento delle funzioni nell'intervallo che ho indicato.

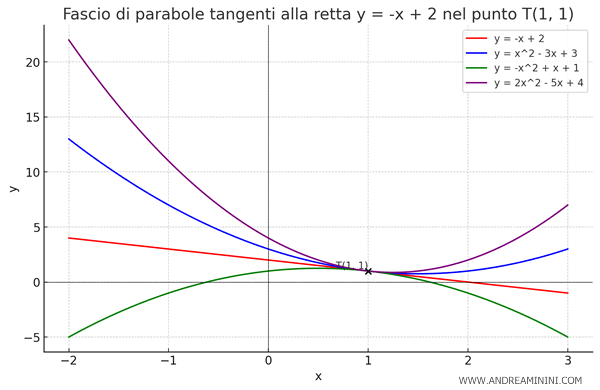
In questo caso il grafico è un fascio di parabole tangenti a una retta nel punto T.

E così via.