La funzione linalg.eig() di numpy
Per calcolare gli autovettori di una matrice con il linguaggio python, uso la funzione linalg.eig del modulo numpy.
linalg.eig(x)
L'argomento x è una matrice quadrata precedentemente definita tramite la funzione array.
La funzione linalg.eig calcola gli autovettori della matrice.
Cosa sono gli autovettori? Nel calcolo matriciale un autovettore di una funzione tra spazi vettoriali è un vettore non nullo tale chel'immagine della funzione è il vettore stesso moltiplicato per un numero detto autovalore. Per un approfondimento sugli autovettori.
Un esempio pratico
La funzione linalg.eig appartiene al modulo numpy.
Importo il modulo numpy nell'interprete python tramite l'istruzione import.
import numpy as np
Definisco una matrice tramite l'istruzione array() di numpy.
m=np.array([[2,1],[1,2]])
Si tratta di una matrice quadrata.
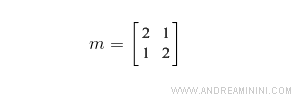
Uso la funzione linalg.eig() per calcolare gli autovettori.
np.linalg.eig(m)
La funzione restituisce gli autovalori e gli autovettori della matrice.
(array([3., 1.]), array([[ 0.70710678, -0.70710678], [ 0.70710678, 0.70710678]]))
Per separare gli autovalori e gli autovettori assegno i valori a due variabili diverse
autovalori, autovettori =np.linalg.eig(m)
In questo modo nella variabile autovalori memorizzo la lista dei due autovalori della matrice λ1=3 e λ2=1.
>>> autovalori
array([3., 1.])
Nella variabile autovettori memorizzo gli array degli autovettori della matrice
>>> autovettori
array([[ 0.70710678, -0.70710678],
[ 0.70710678, 0.70710678]])
Nella matrice gli autovettori sono in colonna. E' importante ricordarlo.

A questo punto verifico se il calcolo è corretto
Verifica
Il primo autovettore nella prima colonna è il seguente
>>> autovettori[:,0]
array([0.70710678, 0.70710678])
Calcolo il prodotto tra la matrice e l'autovettore
>>> np.dot(m, autovettori[:,0])
array([2.12132034, 2.12132034])
Ora calcolo il prodotto tra l'autovettore e l'autovalore
>>> autovettori[:,0]*autovalori[0]
array([2.12132034, 2.12132034])
Il risultato è lo stesso, quindi il calcolo è corretto.
Il secondo autovettore nella seconda colonna è il seguente
>>> autovettori[:,1]
array([-0.70710678, 0.70710678])
Calcolo il prodotto tra la matrice e l'autovettore
>>> np.dot(matrice, autovettori[:,0])
array([-0.70710678, 0.70710678])
Ora calcolo il prodotto tra l'autovettore e l'autovalore
>>> autovettori[:,0]*autovalori[0]
array([-0.70710678, 0.70710678])
Il risultato è lo stesso, quindi il calcolo è corretto.
E così via.
