Come trovare la durata minima del progetto

Uno dei problemi della schedulazione di un progetto (project scheduling) è il calcolo della durata minima di un progetto. Per trovarla posso usare l'algoritmo che trova il costo massimo del cammino orientato in un digrafo aciclico.

Un esempio pratico

Un progetto è composto da 14 attività.

Alcune attività devono rispettare un vincolo di precedenza rispetto alle altre, ossia possono iniziare solo al termine di altre attività.

Attività	Durata	Vincoli di precedenza
A1	7	--
A2	9	--
A3	12	--
A4	16	A1, A2
A5	15	A1, A2, A3
A6	14	A1, A2
A7	6	A4, A6
A8	3	A5, A6
A9	5	A6
A10	7	A9
A11	8	A7
A12	9	A10, A11
A13	11	A8, A9
A14	6	A10, A13

Nota. Le attività sono numerate in modo tale che nessu indice è inferiore agli indici dei vincoli di precedenza.

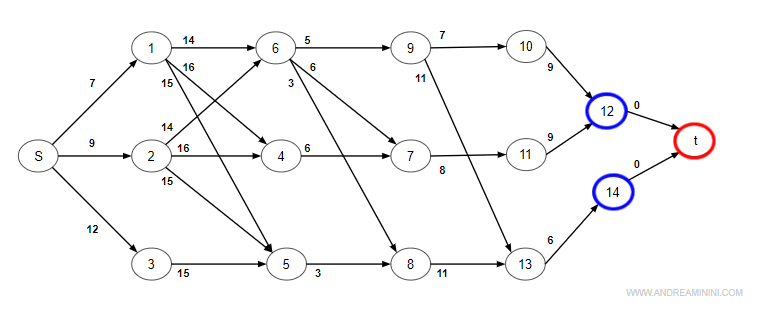
Come prima cosa costruisco un digrafo (grafo orientato) cominciando dal nodo iniziale start (s) fino al nodo finale (t).

I nodi sono le attività del progetto mentre gli archi indicano i vincoli di precedenza tra le attività.

Sopra ogni arco indico la durata dell'attività di arrivo espressa in giorni.

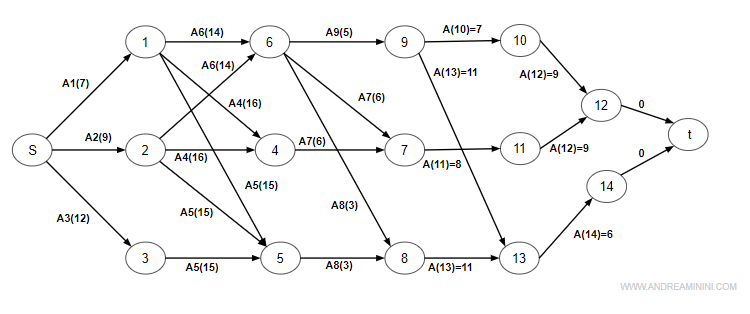
Nota. Il nodo di inizio (s) e fine progetto (t) hanno durata pari a zero.

Per trovare la durata minima applico l'algoritmo a partire dal nodo S.

Analizzo ogni singolo nodo in ordine topologico, quindi in sequenza n=1, 2, 3, 4 ecc.

Per ciascun nodo trovo il tempo massimo T(n)+D(n) dei cammini in entrata e il nodo predecessore P(n).

Il nodo terminale t indica la fine del progetto.

Nodo 1 (attività di durata 7)

Il nodo 1 ha un solo arco in entrata da S

$$ T(1)_{min} = T(S) + D(S) = 0 + 0 = 0$$

$$ P(1) = S $$

Quindi, l'attività A1 può iniziare subito nell'istante zero (tempo minimo).

Nodo 2 (attività di durata 9)

Il nodo 2 ha un solo arco in entrata da S

$$ T(2)_{min} = T(S) + D(S) = 0 + 0 = 0 $$

$$ P(2) = S $$

Quindi, l'attività A2 può iniziare subito nell'istante zero (tempo minimo).

Nodo 3 (attività di durata 12)

Il nodo 3 ha un solo arco in entrata da S

$$ T(2)_{min} = T(S) + D(S) = 0 + 0 = 0 $$

$$ P(3) = S $$

Quindi, l'attività A3 può iniziare subito nell'istante zero (tempo minimo).

Nodo 4 (attività di durata 16)

Il nodo 4 ha due archi in entrata dal nodo 1 e dal nodo 2

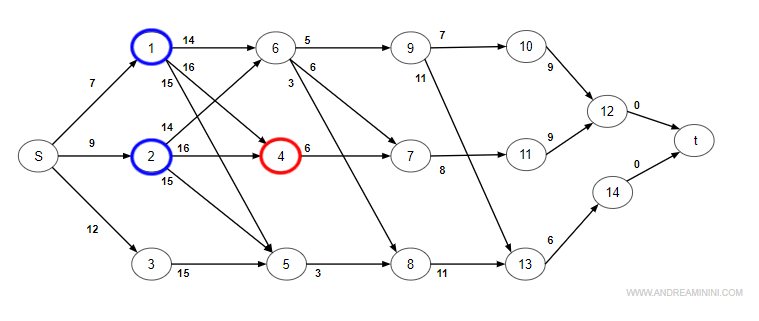
Scelgo il tempo maggiore.

$$ max \begin{cases} T(4)_{min} = T(1) + D(1) = 0 + 7 = 7 \\ T(4)_{min} = T(2) + D(2) = 0 + 9 = 9 \end{cases} $$

Il percorso con tempo maggiore è quello proveniente dal nodo 2.

Quindi, prima dell'istante t=9 giorni l'attività A4 non può iniziare (tempo minimo).

$$ T(4)_{min} =9 $$

$$ P(4) = 2 $$

Nodo 5 (attività di durata 15)

Il nodo 5 ha tre archi in entrata dal nodo 1, dal nodo 2 e dal nodo 3

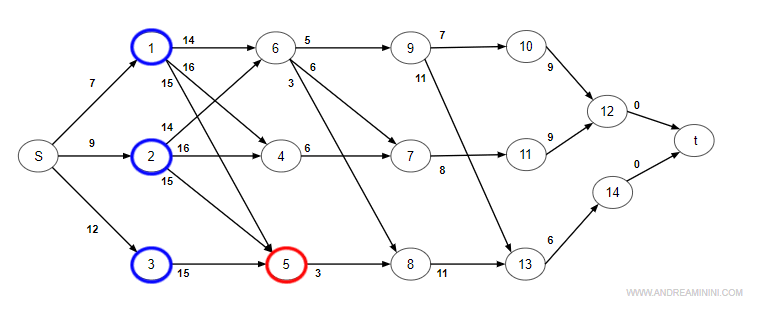
Scelgo il tempo maggiore.

$$ max \begin{cases} T(5)_{min} = T(1) + D(1) = 0 + 7 = 7 \\ T(5)_{min} = T(2) + D(2) = 0 + 9 = 9 \\ T(5)_{min} = T(3) + D(3) = 0 + 12 = 12 \end{cases} $$

Il percorso con tempo maggiore è quello proveniente dal nodo 3.

Quindi, prima dell'istante t=12 giorni l'attività A5 non può iniziare (tempo minimo).

$$ T(5)_{min} =12 $$

$$ P(5) = 3 $$

Nodo 6 (attività di durata 14)

Il nodo 6 ha due archi in entrata dal nodo 1 e dal nodo 2.

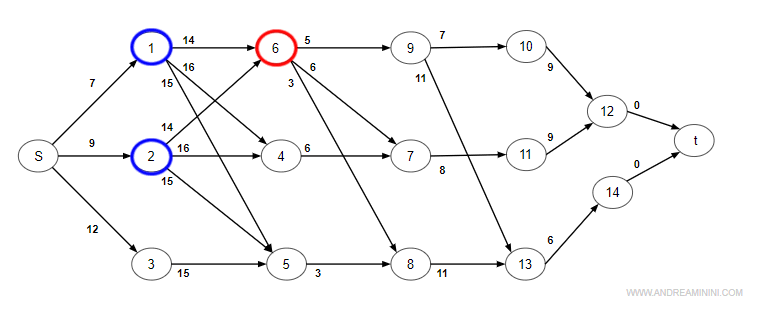
Scelgo il tempo maggiore.

$$ max \begin{cases} T(6)_{min} = T(1) + D(1) = 0 + 7 = 7 \\ T(6)_{min} = T(2) + D(2) = 0 + 9 = 9 \end{cases} $$

Il percorso con tempo maggiore è quello proveniente dal nodo 2.

Quindi, prima dell'istante t=9 giorni l'attività A6 non può iniziare (tempo minimo).

$$ T(6)_{min} =9 $$

$$ P(5) = 2 $$

Nodo 7 (attività di durata 6)

Il nodo 7 ha due archi in entrata dal nodo 4 e dal nodo 6.

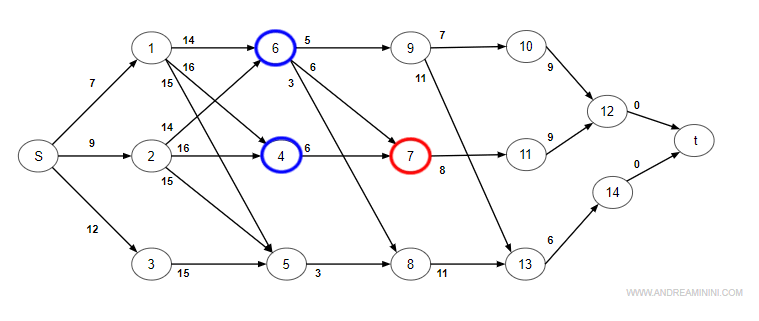
Scelgo il tempo maggiore.

$$ max \begin{cases} T(7)_{min} = T(4) + D(4) = 9 + 16 = 25 \\ T(4)_{min} = T(6) + D(6) = 9 + 14 = 23 \end{cases} $$

Il percorso con tempo maggiore è quello proveniente dal nodo 4.

Quindi, prima dell'istante t=25 giorni l'attività A7 non può iniziare (tempo minimo).

$$ T(7)_{min} =25 $$

$$ P(7) = 4 $$

Nodo 8 (attività di durata 3)

Il nodo 8 ha due archi in entrata dal nodo 5 e dal nodo 6.

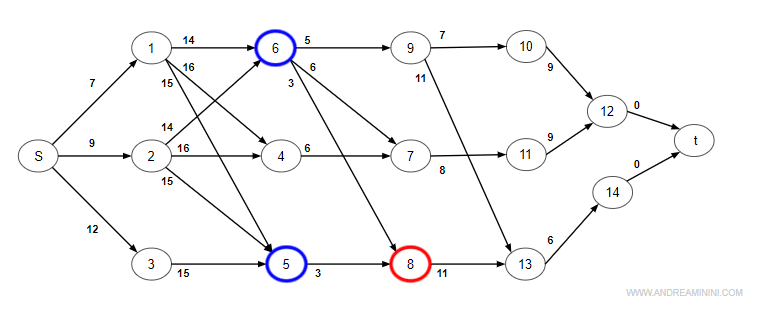
Scelgo il tempo maggiore.

$$ max \begin{cases} T8)_{min} = T(5) + D(5) = 12 + 15 = 27 \\ T(5)_{min} = T(6) + D(6) = 9 + 14 = 23 \end{cases} $$

Il percorso con tempo maggiore è quello proveniente dal nodo 5.

Quindi, prima dell'istante t=27 giorni l'attività A8 non può iniziare (tempo minimo).

$$ T(8)_{min} =T(5) + D(5) = 12+15 =27 $$

$$ P(8) = 5 $$

Nodo 9 (attività di durata 5)

Il nodo 9 ha un solo arco in entrata dal nodo 6.

$$ T(9)_{min} =T(6) + D(6) = 9 + 14 =23 $$

$$ P(9) = 6 $$

Quindi, prima dell'istante t=23 giorni l'attività A9 non può iniziare (tempo minimo).

Nodo 10 (attività di durata 7)

Il nodo 10 ha un solo arco in entrata dal nodo 9.

$$ T(10)_{min} =T(9) + D(9) = 23 + 5 =28 $$

$$ P(10) = 9 $$

Quindi, prima dell'istante t=28 giorni l'attività A10 non può iniziare (tempo minimo).

Nodo 11 (attività di durata 8)

Il nodo 11 ha un solo arco in entrata dal nodo 7.

$$ T(11)_{min} =T(7) + D(7) = 25 + 6 =31 $$

$$ P(11) = 7 $$

Quindi, prima dell'istante t=31 giorni l'attività A11 non può iniziare (tempo minimo).

Nodo 12 (attività di durata 9)

Il nodo12 ha due archi in entrata dal nodo 10 e dal nodo 11.

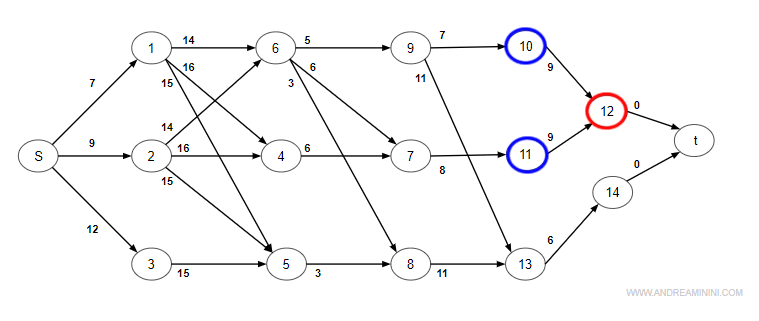
Scelgo il tempo maggiore.

$$ max \begin{cases} T(12)_{min} = T(10) + D(10) =28 + 7 = 35 \\ T(12)_{min} = T(11) + D(11) = 31 + 8 = 39 \end{cases} $$

Il percorso con tempo maggiore è quello proveniente dal nodo 11.

Quindi, prima dell'istante t=39 giorni l'attività A12 non può iniziare (tempo minimo).

$$ T(12)_{min} =39 $$

$$ P(12) = 11 $$

Nodo 13 (attività di durata 11)

Il nodo13 ha due archi in entrata dal nodo 9 e dal nodo 8.

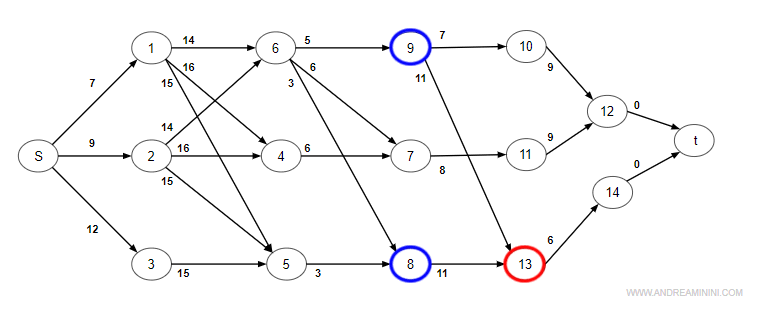
Scelgo il tempo maggiore.

$$ max \begin{cases} T(13)_{min} = T(8) + D(8) =27 + 3 = 30 \\ T(13)_{min} = T(9) + D(9) = 23+ 5 = 28 \end{cases} $$

Il percorso con tempo maggiore è quello proveniente dal nodo 8.

Quindi, prima dell'istante t=39 giorni l'attività A13 non può iniziare (tempo minimo).

$$ T(13)_{min} =30 $$

$$ P(13) =8 $$

Nodo 14 (attività di durata 6)

Il nodo 14 ha un solo arco in entrata dal nodo 13.

$$ T(14)_{min} =T(13) + D(13) = 30 + 11 =41 $$

$$ P(14) = 13 $$

Quindi, prima dell'istante t=41 giorni l'attività A14 non può iniziare (tempo minimo).

Nodo t (attività di durata 0)

Il nodo finale t ha due archi in entrata dal nodo 12 e dal nodo 14.

Scelgo il tempo maggiore.

$$ max \begin{cases} T(t)_{min} = T(12) + D(12) =39 + 9 = 48 \\ T(t)_{min} = T(14) + D(14) = 41+ 6 = 47 \end{cases} $$

Il percorso con tempo maggiore è quello proveniente dal nodo 12.

Quindi, prima dell'istante t=48 giorni il progetto non può finire (tempo minimo).

$$ T(t)_{min} =48 $$

$$ P(t) =12 $$

In conclusione, la soluzione del problema è la seguente:

La durata minima del progetto è 48 giorni.

Ecco il tempo minimo di inizio (Tmin) per ciascuna attività del progetto

Attività	Durata	Vincoli di precedenza	Tmin
A1	7	--	0
A2	9	--	0
A3	12	--	0
A4	16	A1, A2	9
A5	15	A1, A2, A3	12
A6	14	A1, A2	9
A7	6	A4, A6	25
A8	3	A5, A6	27
A9	5	A6	23
A10	7	A9	28
A11	8	A7	31
A12	9	A10, A11	39
A13	11	A8, A9	30
A14	6	A10, A13	41

Una volta calcolata la durata minima del progetto e i tempi minimi di inizio delle attività, posso calcolare i tempi massimi di fine attività e trovare le attività critiche del progetto.

E così via.