Come trovare le attivitÓ critiche di un progetto
Nel project scheduling posso individuare le attività critiche di un progetto tramite l'algoritmo che calcola il costo massimo del cammino in un grafo orientato senza cicli.
- Costruisco il digrafo del progetto
- Calcolo i tempi minimi delle attività (inizio al più presto)
- Calcolo la durata minima del progetto
- Calcolo i tempi massimi delle attività (fine al più tardi)
- Calcolo il tempo di slittamento di ogni attività
- Le attività con tempo di slittamento pari a zero sono attività critiche
Nota. Nel progetto ogni singola attività deve essere assegnata a una durata di tempo. Le attività possono avere vincoli di precedenza con altre attività del progetto o meno.
Un esempio pratico
Un progetto è suddiviso in 14 attività.
Ogni attività ha una durata precisa, indicata in giorni, ed eventualmente dei vincoli di precedenza con altre attività.
| Attività | Durata | Vincoli di precedenza |
|---|---|---|
| A1 | 7 | -- |
| A2 | 9 | -- |
| A3 | 12 | -- |
| A4 | 16 | A1, A2 |
| A5 | 15 | A1, A2, A3 |
| A6 | 14 | A1, A2 |
| A7 | 6 | A4, A6 |
| A8 | 3 | A5, A6 |
| A9 | 5 | A6 |
| A10 | 7 | A9 |
| A11 | 8 | A7 |
| A12 | 9 | A10, A11 |
| A13 | 11 | A8, A9 |
| A14 | 6 | A10, A13 |
Per prima cosa, costruisco un grafo per rappresentare le attività.
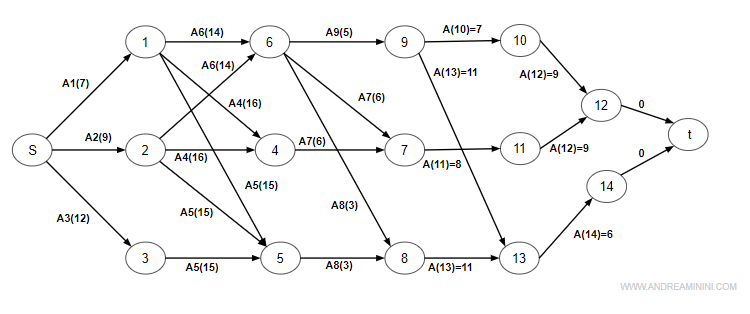
Gli archi del grafo sono le attività e, tra parentesi, indico la durata dell'attività.
I nodi identificano gli stati del progetto, o fine attività, enumerati in modo da seguire un ordine logico.
Nota. Il nodo iniziale (s) indica l'inizio del progetto mentre il nodo finale (t) la fine del progetto.
A questo punto calcolo i tempi minimi Tmin per ciascuna attività e la durata minima del progetto.
Il tempo minimo indica l'istante di tempo più basso (quanto più presto) in cui può cominciare un'attività.
E' l'istante di inizio al più presto.
In questo caso la durata minima del progetto è di 48 giorni.
| Attività | Durata | Vincoli di precedenza | Tmin |
|---|---|---|---|
| A1 | 7 | -- | 0 |
| A2 | 9 | -- | 0 |
| A3 | 12 | -- | 0 |
| A4 | 16 | A1, A2 | 9 |
| A5 | 15 | A1, A2, A3 | 12 |
| A6 | 14 | A1, A2 | 9 |
| A7 | 6 | A4, A6 | 25 |
| A8 | 3 | A5, A6 | 27 |
| A9 | 5 | A6 | 23 |
| A10 | 7 | A9 | 28 |
| A11 | 8 | A7 | 31 |
| A12 | 9 | A10, A11 | 39 |
| A13 | 11 | A8, A9 | 30 |
| A14 | 6 | A10, A13 | 41 |
Nota . Per vedere l'algoritmo di calcolo della durata minima del progetto e degli istanti iniziali (tempi minimi) di ciascuna attività rimando alla lettura degli appunti su come trovare la durata minima del progetto.
Assegno la durata di ogni arco alle variabili cda,a
$$ c_{s,1} = 7 \\ c_{s,2} = 9 \\ c_{s,3} = 11 \\ c_{1,6} = 14 \\ c_{1,4} = 16 \\ c_{1,5} = 15 \\ c_{2,6} = 14 \\ c_{2,4} = 16 \\ c_{2,5} = 15 \\ c_{6,9} = 5 \\ c_{6,7} = 6 \\ c_{6,8} = 3 \\ c_{4,7} = 6 \\ c_{5,8} = 3 \\ c_{9,10} = 7 \\ c_{9,13} = 11 \\ c_{7,11} = 8 \\ c_{8,13} = 11 \\ c_{10,12} = 9 \\ c_{11,12} = 9 \\ c_{13,14} = 6 \\ c_{12,t} = 0 \\ c_{14,t} = 0 $$
L'algoritmo elabora i nodi a ritroso dal nodo terminale t a quello iniziale s/.
Per ciascuno nodo calcolo il tempo massimo Tmax in cui può terminare un'attività, senza pregiudicare la durata complessiva del progetto.
$$ T_{max}(x) = \min (T_{max}(y) - c_{x,y} $$
Nota. Dove x è un nodo qualsiasi e y sono i nodi che raggiunge con degli archi in uscita. Mentre cx,y è il tempo necessario per passare dal nodo x al nodo y.
Il tempo massimo indica l'istante di tempo più alto (quanto più tardi) può terminare un'attività.
E' l'istante di fine al più tardi.
Nodo t
Il nodo t è assegnato alla durata del progetto, ossia 48.
$$ T_{max}(t) = 48 $$
Nodo 14
Il nodo 14 ha un solo arco in uscita verso il nodo t con una durata fittizia pari a 0.
$$ T_{max}(14) = T_{max}(t) - c_{14,t} = 48 - 0 = 48 $$
Questo vuol dire che il tempo massimo in cui può verificarsi l'attività A14 è 48 giorni.
Nodo 13
Il nodo 13 ha un solo arco in uscita verso il nodo 14 con una durata pari a 6 giorni.
$$ T_{max}(13) = T_{max}(14) - c_{13,14} = 48 - 6 = 42 $$
Pertanto, l'attività 13 deve verificarsi al massimo entro 42 giorni dall'inizio del progetto.
Nodo 12
Il nodo 12 ha un solo arco in uscita verso il nodo t con una durata fittizia pari a 0.
$$ T_{max}(12) = T_{max}(t) - c_{12,t} = 48 - 0 = 48 $$
Questo vuol dire che l'istante massimo in cui deve essere ultimata l'attività A12 è 48 giorni.
Nodo 11
Il nodo 11 ha un solo arco in uscita verso il nodo 12 con una durata 9 giorni.
$$ T_{max}(11) = T_{max}(12) - c_{11,12} = 48 - 9 = 39 $$
L'istante massimo in cui l'attività A11 deve essere ultimata è il 39-esimo giorno da inizio progetto.
Nodo 10
Il nodo 10 ha un arco in uscita verso il nodo 12 con una durata di 9 giorni.
$$ T_{max}(10) = T_{max}(12) - c_{10,12} = 48 - 9 = 39 $$
Pertanto, l'attività A10 deve essere ultimata entro il giorno 39 da inizio progetto.
Nodo 9
Il nodo 9 ha due archi in uscita, verso il nodo 10 con una durata di 7 giorni e verso il nodo 13 con una durata di 11 giorni.
Scelgo il valore minimo tra i due valori ossia 31.
$$ T_{max}(10) = min \begin{cases} T_{max}(10) - c_{9,10} = 39 - 7 = 32 \\ T_{max}(13) - c_{9,13} = 42 - 11 = 31 \end{cases} $$
$$ T_{max}(10) = 31 $$
Pertanto, l'attività A9 deve essere ultimata entro il giorno 31 dall'inizio del progetto.
Nodo 8
Il nodo 8 ha un arco in uscita verso il nodo 13 con una durata di 11 giorni.
$$ T_{max}(8) = T_{max}(13) - c_{8,13} = 42 - 11 = 31 $$
Pertanto, l'attività A8 deve essere ultimata entro il giorno 31 da inizio progetto.
Nodo 7
Il nodo 7 ha un arco in uscita verso il nodo 11 con una durata di 8 giorni.
$$ T_{max}(7) = T_{max}(11) - c_{7,11} = 39 - 8 = 31 $$
Pertanto, l'attività A7 deve essere ultimata entro il giorno 31 da inizio progetto.
Nodo 6
Il nodo 6 ha tre archi in uscita, verso il nodo 9 con una durata di 6 giorni, verso il nodo 7 con una durata di 6 giorni, verso il nodo 8 con una durata di 3 giorni.
Scelgo il valore minimo tra i valori ossia 31.
$$ T_{max}(6) = min \begin{cases} T_{max}(9) - c_{6,9} = 31 - 5 = 26 \\ T_{max}(7) - c_{6,7} = 31 - 6 = 25 \\ T_{max}(8) - c_{6,8} = 31 - 3 = 28 \end{cases} $$
$$ T_{max}(6) = 25 $$
Pertanto, l'attività A6 deve essere ultimata entro il giorno 25 dall'inizio del progetto.
Nodo 5
Il nodo 5 ha un arco in uscita verso il nodo 8 con una durata di 3 giorni.
$$ T_{max}(5) = T_{max}(8) - c_{5,8} = 31 - 3 = 28 $$
Pertanto, l'attività A5 deve essere ultimata al più entro il giorno 28 da inizio progetto.
Nodo 4
Il nodo 4 ha un arco in uscita verso il nodo 7 con una durata di 6 giorni.
$$ T_{max}(4) = T_{max}(7) - c_{4,7} = 31 - 6 = 25 $$
Pertanto, l'attività A4 deve essere ultimata al massimo entro il giorno 25 da inizio progetto.
Nodo 3
Il nodo 3 ha un arco in uscita verso il nodo 5 con una durata di 15 giorni.
$$ T_{max}(3) = T_{max}(5) - c_{3,5} = 28 - 15 = 13 $$
Pertanto, l'attività A3 deve essere ultimata al massimo entro il giorno 13 da inizio progetto.
Nodo 2
Il nodo 2 ha tre archi in uscita, verso il nodo 6 con una durata di 14 giorni, verso il nodo 4 con una durata di 16 giorni, verso il nodo 5 con una durata di 15 giorni.
Scelgo il valore minimo tra i valori ossia 9.
$$ T_{max}(2) = min \begin{cases} T_{max}(6) - c_{2,6} = 25 - 14 = 11 \\ T_{max}(4) - c_{2,4} = 25 - 16 = 9 \\ T_{max}(5) - c_{2,5} = 28 - 15 = 13 \end{cases} $$
$$ T_{max}(2) = 9 $$
Pertanto, l'attività A2 deve essere ultimata entro il giorno 9 dall'inizio del progetto.
Nodo 1
Il nodo 2 ha tre archi in uscita, verso il nodo 6 con una durata di 14 giorni, verso il nodo 4 con una durata di 16 giorni, verso il nodo 5 con una durata di 15 giorni.
Scelgo il valore minimo tra i valori ossia 9.
$$ T_{max}(1) = min \begin{cases} T_{max}(6) - c_{1,6} = 25 - 14 = 11 \\ T_{max}(4) - c_{1,4} = 25 - 16 = 9 \\ T_{max}(5) - c_{1,5} = 28 - 15 = 13 \end{cases} $$
$$ T_{max}(1) = 9 $$
Pertanto, l'attività A1 deve essere ultimata entro il giorno 9 dall'inizio del progetto.
Ho ottenuto tutti gli istanti massimi Tmax delle attività.
| Attività | Durata | Vincoli di precedenza | Tmin | Tmax |
|---|---|---|---|---|
| A1 | 7 | -- | 0 | 9 |
| A2 | 9 | -- | 0 | 9 |
| A3 | 12 | -- | 0 | 13 |
| A4 | 16 | A1, A2 | 9 | 25 |
| A5 | 15 | A1, A2, A3 | 12 | 28 |
| A6 | 14 | A1, A2 | 9 | 25 |
| A7 | 6 | A4, A6 | 25 | 31 |
| A8 | 3 | A5, A6 | 27 | 31 |
| A9 | 5 | A6 | 23 | 31 |
| A10 | 7 | A9 | 28 | 39 |
| A11 | 8 | A7 | 31 | 39 |
| A12 | 9 | A10, A11 | 39 | 48 |
| A13 | 11 | A8, A9 | 30 | 42 |
| A14 | 6 | A10, A13 | 41 | 48 |
Nota. I valori Tmin sono i tempi minimi che indicano l'istante di inizio al più presto dell'attività. I valori Tmax sono i tempi massimi che indicano l'istante di fine al più tardi dell'attività.
Una volta trovati i tempi minimi (minimo inizio) e i tempi massimi (massima fine), li indico sopra ogni nodo del grafo tra parentesi tonde.
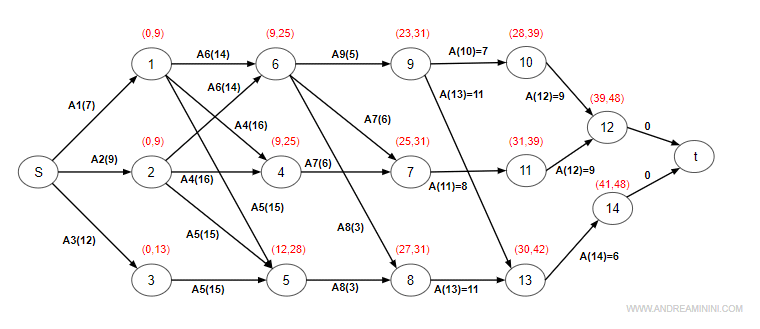
A questo punto calcolo il tempo di slittamento Ts di ciascuna attività.
E' il lasso di tempo in cui l'inizio e la fine dell'attività possono slittare a causa di un ritardo, senza pregiudicare la durata complessiva del progetto.
$$ T_s = (T_{max} - d) - T_{min} $$
Dove d è la durata dell'attività, Tmin è il tempo di inizio al più presto e Tmax il tempo di fine al più tardi.
| Attività | Durata(d) | Vincoli di precedenza | Tmin | Tmax | Ts=Tmax-d-Tmin |
|---|---|---|---|---|---|
| A1 | 7 | -- | 0 | 9 | 2 |
| A2 | 9 | -- | 0 | 9 | 0 |
| A3 | 12 | -- | 0 | 13 | 1 |
| A4 | 16 | A1, A2 | 9 | 25 | 0 |
| A5 | 15 | A1, A2, A3 | 12 | 28 | 1 |
| A6 | 14 | A1, A2 | 9 | 25 | 2 |
| A7 | 6 | A4, A6 | 25 | 31 | 0 |
| A8 | 3 | A5, A6 | 27 | 31 | 1 |
| A9 | 5 | A6 | 23 | 31 | 3 |
| A10 | 7 | A9 | 28 | 39 | 4 |
| A11 | 8 | A7 | 31 | 39 | 0 |
| A12 | 9 | A10, A11 | 39 | 48 | 0 |
| A13 | 11 | A8, A9 | 30 | 42 | 1 |
| A14 | 6 | A10, A13 | 41 | 48 | 1 |
Le attività con tempo di slittamento Ts=0 sono le attività critiche del progetto.
In conclusione, le attività critiche del progetto sono A2, A4, A7, A11, A12.
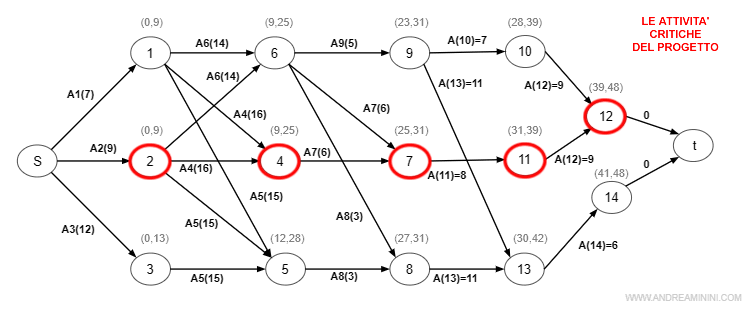
Un eventuale ritardo, anche minimo, in queste attività causa un ritardo all'intero progetto.
Sono le attività da seguire con maggiore attenzione.
E così via.
