Aggiornamento di Bellman

L'aggiornamento di Bellman contrae il vettore delle utilità stimate U degli stati, a partire da un valore iniziale di default, avvicinandolo al valore reale delle utilità.

A cosa serve? E' utilizzato nell'algoritmo di iterazione di valori per consentire all'agente razionale di prendere decisioni complesse e risolvere problemi di cui non possiede tutte le informazioni.

Dopo ogni iterazione x dell'algoritmo, il vettore delle utilità Ux è sempre più vicino al vettore reale delle utilità U degli stati.

Come funziona l'aggiornamento di Bellman

Dal punto di vista matematico l'aggiornamento di Bellman può essere visto come una funzione matematica B.

U_x+1=B(U_x)

L'argomento in input della funzione è il vettore delle utilità U_x al ciclo x.

Il risultato in output è il vettore delle utilità U_x+1 dell'iterazione successiva x+1. E così via.

L'aggiornamento di Bellman propaga l'informazione in avanti e comincia un un nuovo ciclo.

Quando termina?

Il processo continua fin quando il vettore Ux eguaglia il vettore delle utilità reali U.

Quali sono i punti di forza dell'algoritmo?

Una prima considerazione importante da fare è che l'aggiornamento di Bellman converge sempre al vettore delle utilità reale degli stati.

Inoltre, è sicuramente un modo più efficiente per trovare la soluzione del problema rispetto all'esplorazione completa di tutte le combinazioni possibili degli stati.

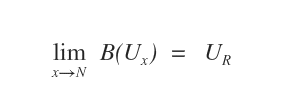
Quello che non sappiamo è quanti cicli ( N ) sono necessari per attuare la convergenza. Il che può diventare un problema.

Quali sono i punti di debolezza?

Se il calcolo è troppo lungo, la soluzione potrebbe arrivare troppo tardi, quando non serve più ( inefficacia ), o il costo di elaborazione diventare eccessivamente alto ( inefficienza ).

E' quindi necessario stimare il numero delle iterazioni N per risolvere il problema.

Poi fare un'analisi costi benefici prima di eseguire il programma.

Come calcolare i cicli dell'algoritmo

Allo stato iniziale (t=0) gli stati hanno tutti lo stesso valore di default ( es. zero ).

Il vettore degli stati iniziale si presenta in questo modo:

U₀(0,0,0,0,....,0)

L'agente non conosce ancora il vettore delle utilità reali (Ur).

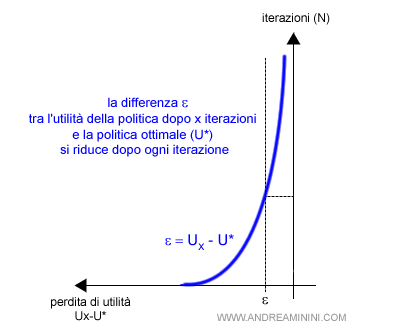
Tuttavia, se lo conoscesse potrebbe calcolare l'errore ε della stima calcolando la differenza U₀-U_R.

ε=U₀-U_R

Il risultato va trasformato in un valore assoluto, sotto modulo, perché non è detto che la differenza U₀-U_R sia positiva (U₀-U_R>0) può anche essere negativa (U₀-U_R<0).

In questo caso, per calcolare l'errore della stima quello che ci interessa è calcolare la differenza tra i due vettori.

ε=|U₀-U_R|

Va poi considerato anche il fattore di sconto γ dell'algoritmo di iterazione dei valori.

ε=γ|E₀-U_R|

Il fattore di sconto γ<1 permette di attribuire maggiore importanza alle prime decisioni rispetto alle azioni successive.

Se invece γ=1 le azioni hanno tutte la stessa importanza, la posizione nella sequenza decisionale non influisce sul calcolo delle utilità.

In quest'ultimo caso (γ=1) l'agente ha una visione temporale più ampia, trova soluzioni più efficaci ma l'algoritmo consuma molte più risorse.

Ora, sappiamo che l'algoritmo di Bellman è convergente.

Quindi l'errore ε dovrebbe ridursi dopo ogni ciclo.

ε1 ≤ ε0

La precedente disequazione può essere riscritta nel seguente modo:

|BU₀-U_R| ≤ γ|U₀-U_R|

Generalizzando la disequazione per i ciclo qualsiasi (i).

|BU_i-U_R| ≤ γ|U_i-U_R|

A questo punto possiamo fare un'altra considerazione. In entrambi i membri della disequazione abbiamo U_i-U_R. Quindi, possiamo eliminarli. Ciò che resta è la seguente:

B ≤ γ

La disequazione vuol dire che ogni iterazione dell'algoritmo di Bellman riduce l'errore ε della stima U_i-U_R di almeno γ.

ε ≤ γ

Sappiamo che le utilità degli stati sono limitate dal sequente valore massimo.

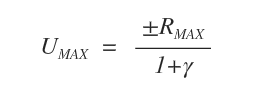
Nota. La variabile R_max indica la massima ricompensa ottenibile dall'agente nella mappa degli stati.

Quindi, l'errore massimo iniziale è il seguente:

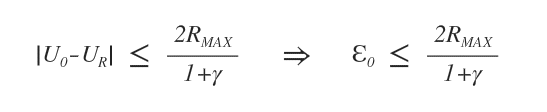
Sappiamo anche che l'errore ε si riduce almeno di γ dopo ogni iterazione.

γ¹ε₁ ≤ ε₀

Generalizzando per ogni iterazione N dell'algoritmo possiamo riscrivere la disequazione nel seguente modo:

γ^Nε ≤ ε

Ora sostituiamo ε al primo membro con la formula del massimo errore possibile.

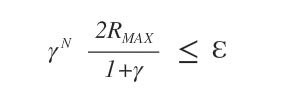
Abbiamo così ottenuto la stima dell'errore di ogni iterazione.

Per calcolare il numero delle iterazioni necessarie per raggiungere un errore ε è sufficiente mettere in evidenza N al membro di sinistra.

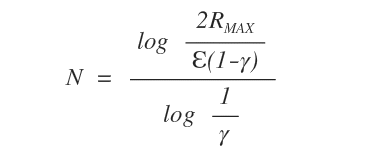
Come si può facilmente intuire, l'algoritmo riduce in modo esponenziale l'errore ε.

Tuttavia, il numero delle iterazioni N cresce in modo esponenziale quando γ si avvicina a 1.

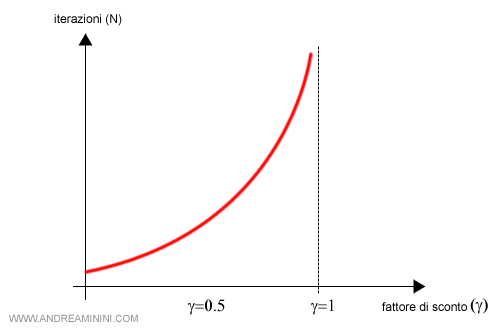
C'è quindi un problema serio da risolvere.

Se γ≅1 il numero dei cicli dell'algoritmo tende a infinito.

Per risolvere questo problema bisogna fissare una condizione di uscita forzata dall'esecuzione.

Esempio. Se i valori delle utilità ( U_t+1 - U_t ) variano poco dopo il t-esimo aggiornamento di Bellman, si deduce che l'utilità degli stati è ormai vicina alla massima utilità ottenibile ( ottimale ). Quindi si può scegliere ed eseguire la politica t-esima perché è già ottimale.