L'algoritmo di iterazione dei valori
L'algoritmo di iterazione dei valori è una tecnica utilizzata per trovare la politica ottimale del processo decisionale di Markov (MDP), ossia la sequenza di azioni per raggiungere un determinato obiettivo, a partire da uno stato iniziale, ottenendo la massima utilità attesa .
- Come funziona l'algoritmo? Si basa su due caratteristiche fondamentali.
- L'utilità di ogni stato è uguale all'utilità attesa delle azioni successive da quel punto in poi, fino al raggiungimento dell'obiettivo finale.
- L'utilità degli stati viene aggiornata più volte, in più cicli ( iterazioni ), fino a trovare la sequenza di azioni migliore per raggiungere l'obiettivo.
Si tratta di un algoritmo iterativo. E' impiegato per risolvere problemi non lineari.
Un esempio pratico
Ad esempio, il bot si trova nella casella B2 e l'obiettivo è raggiungere la casella C2.
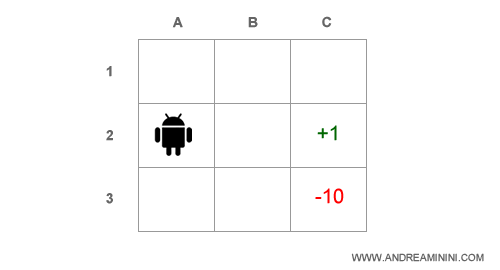
L'utilità dello stato B2 è uguale all'utilità attesa della migliore sequenza di azioni in grado di condurre il bot fino a C2.
Ovviamente, i percorsi possibili per arrivare a C2 a partire da B2 sono molteplici.
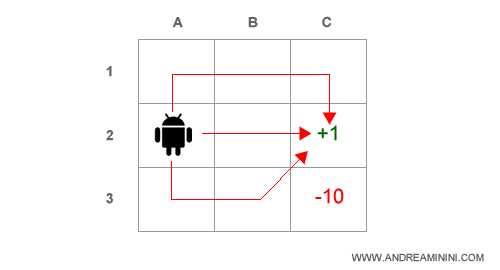
Il valore dello stato B2 è uguale al percorso migliore, quello che restituisce un'utilità attesa più alta degli altri.
Come trovare il percorso migliore? E' uno dei problemi da risolvere. Tuttavia, non è necessario esplorare tutte le combinazioni possibili, perché il processo diventerebbe troppo lungo. Come vedremo, esistono tecniche per trovarlo molto più rapidamente.
Le regole del gioco
Supponiamo che l'agente subisca un costo pari a -0.10, ossia una ricompensa negativa, dopo ogni turno di gioco, fin quando non raggiunge l'obiettivo (C2).
Inoltre, quando l'agente si sposta da una casella all'altra ha un margine di errore del 10% di deviare a destra o a sinistra rispetto alla direzione da seguire.
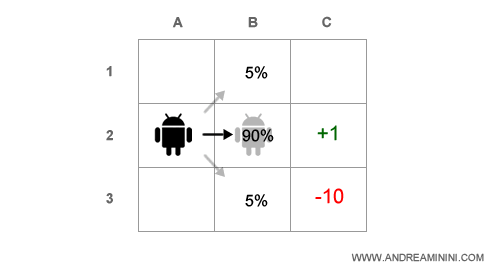
Nelle caselle C2 e C3 il gioco si conclude perché l'agente raggiunge il traguardo (C2) o cade nella trappola (C3).
Come si risolve il problema?
Per risolvere il problema, l'algoritmo MDP deve calcolare l'utilità attesa di n=9 stati ( le nove caselle ).
L'utilità attesa di ogni stato (s) è calcolata con l'equazione di Bellman.
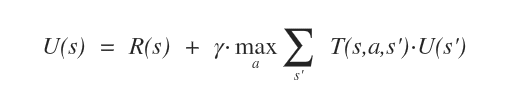
Nota. L'equazione prende il nome di Richard Bellman che per primo ideò questa tecnica di risoluzione iterativa non lineare.
U(s) = utilità dello stato s
R(s) = ricompensa dello stato s
γ =tipo di ricompensa. Per semplicità è impostata a 1 ( ricompensa additiva )
T(s,a,s')=modello di transizione per passare dallo stato s allo stato successivo s'
U(s') = utilità dello stato successivo s'
Ogni equazione ha una sola incognita ed è l'utilità dello stato successivo U(s') e l'algoritmo deve scegliere quello che massimizza l'utilità attesa tra tutti gli stati successivi possibili.
Pertanto, il problema è un sistema composto da 9 equazioni.
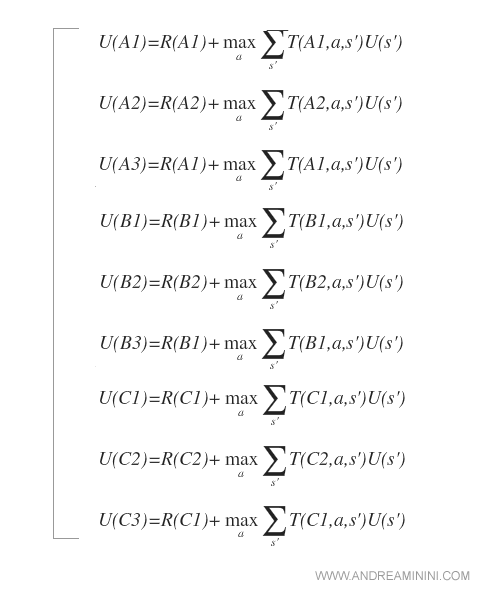
C'è però un problema, le equazioni non sono lineari perché l'operatore max non è lineare.
Non essendo un sistema lineare, non si può ricorrere all'algebra lineare per risolvere questo sistema di equazioni.
Per risolvere il problema occorre utilizzare a una tecnica non lineare iterativa.
Prima iterazione
Alla prima iterazione dell'algoritmo imposto a zero tutti i valori delle utilità U(s) negli n=9 stati che non conosco ancora.
Non avendo informazioni gli assegno un valore di default ( zero ).
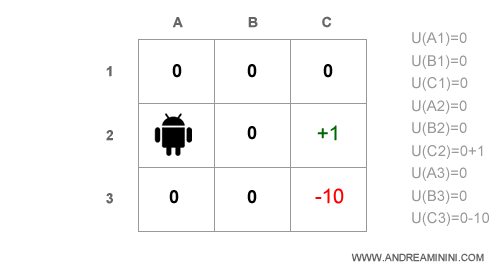
Poi calcolo l'equazione di Bellman in ogni stato.
Ad esempio, nello stato A1 l'agente può muoversi in B1, B2 o A2.

L'equazione di Bellman nello stato A1 è la seguente
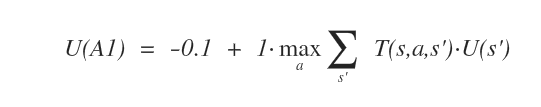
A questo punto calcolo il modello di transizione T(s,a,s') dallo stato A1 considerando il margine di errore del 10%.

Quindi, l'equazione di Bellman nello stato A1 è la seguente:
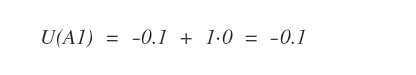
Ora ripeto lo stesso calcolo per tutti gli altri stati.

Il risultato finale è il seguente:
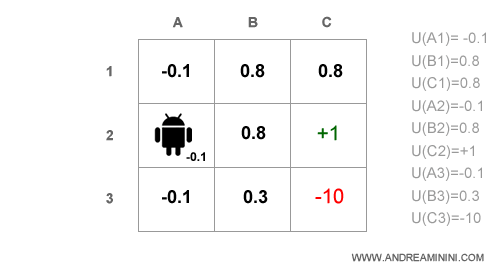
Dopo il primo ciclo di aggiornamento gli stati hanno utilità attese differenti.
Già da adesso si può intravedere un percorso indicativo da A2 a B1 o B2.
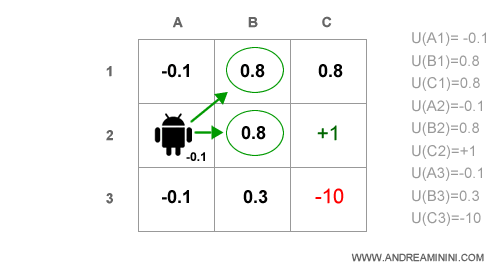
Tuttavia, l'agente non sa ancora se è meglio passare per B1 o B2.
E' quindi necessario lanciare una seconda iterazione.
Nota. Nelle tecniche iterativa non c'è un limite massimo al numero di iterazioni possibili. E' comunque necessario far girare l'algoritmo qualche ciclo per trovare il percorso migliore. Generalmente, una sola iterazione non è sufficiente. Ogni iterazione è detta aggiornamento di Bellman.
Seconda iterazione
Per migliorare le informazioni lancio una seconda iterazione.
Questa volta prendo in considerazione i valori delle utilità nei n=9 stati individuati con la prima iterazione.

Nota. Nella prima iterazione avevo assunto dei valori di default uguali a zero. Nella seconda iterazione, invece, le utilità attese sono diverse. Ogni iterazione propaga l'informazione aggiornata alla successiva iterazione.
Il ricalcolo dell'equazione di Bellman in ognuno dei nove stati modifica le informazioni sull'utilità attesa U(s) perché ogni stato è influenzato dalle utilità attese degli stati vicini.
Ad esempio, nella seconda iterazione l'equazione di Bellman nella casella A1 è la seguente:

Quindi, secondo l'equazione di Bellman l'utilità U(A1) diventa 0.65
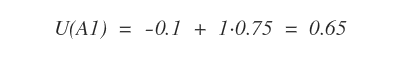
Ora ripeto lo stesso calcolo in tutte le altre caselle ( stati ).
Al termine della seconda iterazione il quadro complessivo è il seguente:
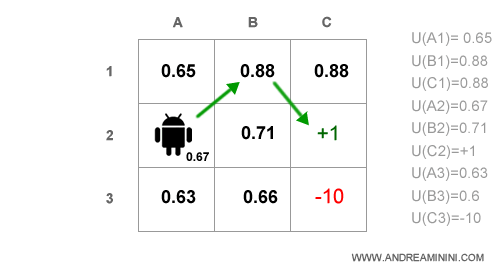
Adesso il percorso ottimale è evidente.
All'agente conviene spostarsi da A2 in B1 (0.88) e poi in C2. Così facendo riduce il rischio di cadere in B3.
L'agente ha così trovato la politica ottimale per risolvere il problema.
Nota. L'algoritmo ha individuato la politica ottimale in due iterazioni. Se avesse cercato la soluzione calcolando ogni percorso possibile da B2 a C2 avrebbe impiegato molto più tempo.
Vantaggi e svantaggi dell'algoritmo iterativo dei valori
L'algoritmo iterativo dei valori consente di trovare la soluzione a un problema MDP non lineare in tempi molto rapidi.
E' senza dubbio più efficiente dell'esplorazione di tutte le combinazioni di percorso possibili a partire dallo stato iniziale.
Esempio. Se l'algoritmo dovesse calcolare l'utilità di tutte le combinazioni di percorso da A2 a C2 impiegherebbe molto più tempo a trovare la politica ottimale.

Inoltre, con il tempo l'algoritmo converge sempre alla politica ottimale.
Dopo ogni iterazione aggiuntiva l'algoritmo si avvicina di più alla politica ottimale (π*).
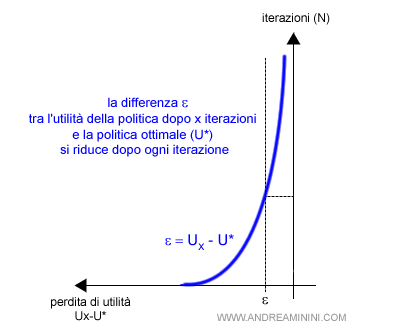
Progressivamente si riduce la perdita di utilità U(πi)-U(π*) dovuta alla differenza tra la politica indicata al ciclo i-esimo (πi) e la politica ottimale (π*).
Quali sono gli svantaggi?
Il numero delle iterazioni necessarie per giungere alla politica ottimale cresce in modo esponenziale rispetto fattore di sconto.
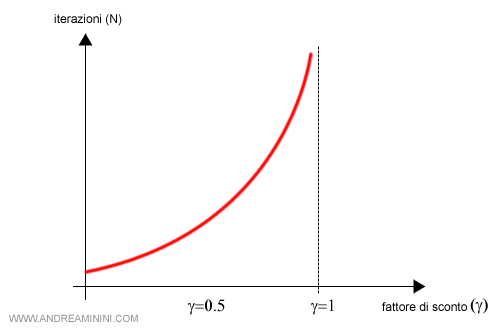
Se il fattore di conto è uguale a uno ( γ=1 ), ossia se le ricompensa è additiva, l'agente deve elaborare la politica su un lungo orizzonte temporale e il numero delle iterazioni N potrebbe diventare insostenibile.
Nota. Il problema non si presenta se l'algoritmo utilizza un fattore di sconto molto basso ( es. γ=0.3 ). Così facendo, però, l'agente diventa miope perché elabora soltanto un'orizzonte temporale limitato in avanti dallo stato corrente. Quindi, la politica trovata potrebbe non essere quella ottimale nel lungo periodo, pur risultando la migliore possibile nel breve periodo.
Per superare questo problema si inserisce nell'algoritmo una condizione di uscita forzata dal ciclo.
L'interruzione del ciclo può essere associata a due eventi:
- Tempo massimo di esecuzione. Dopo un determinato tempo massimo o numeri di cicli, l'algoritmo si interrompe e restituisce l'ultima politica trovata (πi) anche se non è quella ottimale.
Nota. Non è il metodo migliore perché è poco oggettivo. Chi decide qual è il tempo massimo o il numero massimo dei cicli? Nessuno può dirlo a priori.
- Perdita di utilità accettabile. Se un aggiornamento non apporta molte variazioni alle utilità degli stati, allora anche l'errore è piccolo e la differenza tra l'utilità della politica ottimale U(π*) e quella della politica indicata al ciclo i-esimo U(πi) è minima. In questi casi, l'algoritmo può far a meno di eseguire altri cicli alla ricerca della politica ottimale e restituisce la politica accettabile (πi).
Nota. L'algoritmo di iterazione dei valori converge sempre verso la politica ottimale e il margine di errore si riduce progressivamente dopo ogni ciclo. Ad esempio, si può reputare accettabile una politica dopo x cicli (πx) se la perdita di utilità U(π*)-U(πx) è inferiore al 1%.
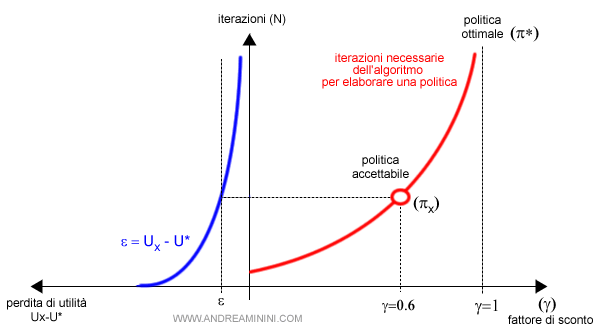
Attenzione. Il precedente diagramma non vuol dire che si deve settare il fattore di sconto γ a 0.6. Dimostra soltanto che dopo x iterazioni la differenza ε tra l'utilità della politica πx e quella ottimale (π*) è quasi nulla. Sarebbe irrazionale continuare con altre iterazioni (x+1) alla ricerca della politica ottimale, in quanto troppo dispendioso in termini di risorse e tempo. Dopo x iterazioni estrapola comunque una politica quasi ottimale ( politica accettabile ). Pur essendo tarato a un fattore di sconto γ=1 ( visione di lungo periodo ) ha una complessità simile a uno configurato a γ=0.6 ( visione di medio-breve periodo ). E' quindi più efficiente ed è efficace in modo accettabile. Per un approfondimento matematico sull'aggiornamento di Bellman.
Pseudocodice dell'algoritmo
Lo pseudocodice finale dell'algoritmo è il seguente:
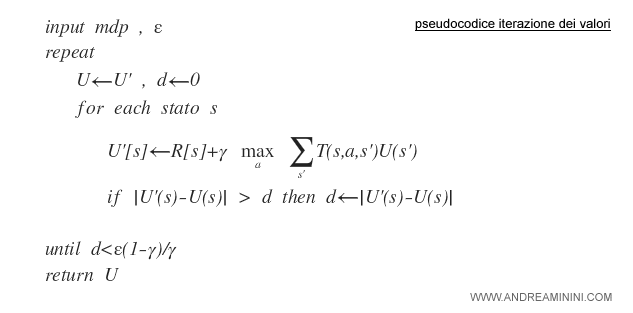
Dove mdp è l'insieme della mappa degli stati S e un modello di transizione T, mentre la variabile ε in input indica l'errore che consideriamo accettabile per una politica quasi-ottimale.
