Il processo decisionale di Markov
Il processo decisionale di Markov ( Markov Decision Process o MDP ) è un modello di transizione dell'agente razionale. Si utilizza in un ambiente dinamico e non deterministico in condizioni di incertezza.
Cosa significa? Quando l'agente razionale prende una decisione, non è detto che gli attuatori robotici eseguano l'azione richiesta dall'intelligenza artificiale, il sistema potrebbe riprodurre per errore un'azione diversa, oppure eseguono l'azione corretta ma alcuni fattori esogeni imprevisti ne modificano il risultato finale. Quindi, per ogni azione c'è un margine di errore da considerare.
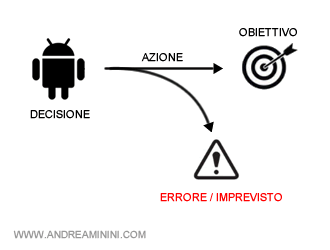
Cos'è il modello decisionale di Markov
Un processo è detto markoviano quando la decisione dipende soltanto dallo stato corrente S dell'agente.
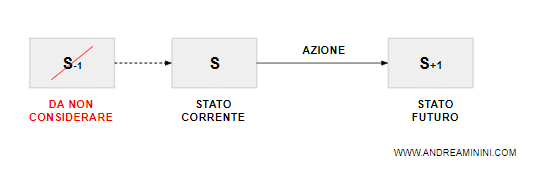
In un processo markoviano la variabile aleatoria è determinata dallo stato corrente.
Nota. Non sono presi in considerazione gli stati storici precedenti S-1, S-2, ecc. In altri termini, gli stati passati non influenzano la decisione corrente.
Come funziona il processo decisionale di Markov
A ogni stato S sono associate delle azioni possibili ( A e B ) che l'agente razionale può scegliere.
Ogni azione conduce a uno stato futuro differente ( S' e S" )
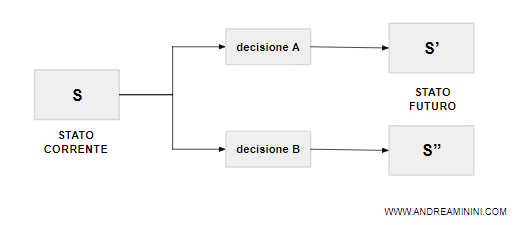
Il precedente schema è un modello deterministico perché ogni azione conduce al 100% a uno stato successivo predeterminato.
In realtà, ogni azione A soltanto ha una probabilità di condurre allo stato successivo desiderato S'.
C'è anche il rischio che l'azione conduca a uno stato diverso Sx.
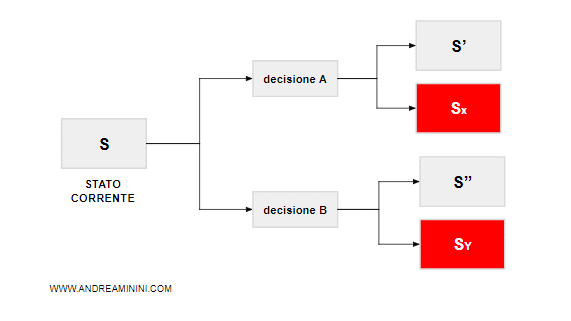
Quest'ultimo schema è un modello probabilistico ed è più adeguato ad affrontare decisioni in regime di incertezza.
Oltre alla probabilità di raggiungere l'obiettivo (S'), c'è anche il rischio di cadere in uno stato peggiore (Sx).
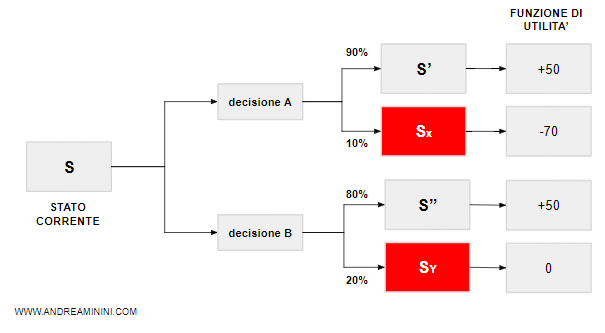
Esempio. Prima di decidere, l'agente deve valutare le conseguenze sulla funzione di utilità di ogni possibile stato successivo. La decisione A e B offrono lo stesso miglioramento in termini di utilità (+50). La decisione A ha una probabilità di successo più alta rispetto a B (90% contro 80%). Tuttavia, la decisione A non è la migliore se si considerano anche i rischi ( -70 nel 10% dei casi ). La decisione B è l'opzione migliore perché offre l'utilità attesa maggiore (EU=40).
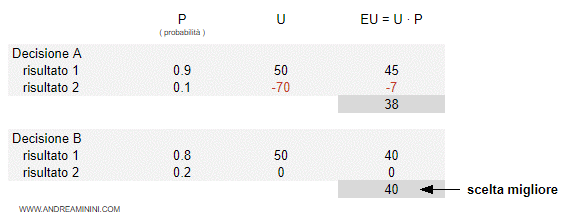
In conclusione, in un processo MDP l'agente razionale deve decidere considerando sia la probabilità di successo che il rischio di ogni azione.
La funzione di ricompensa
Un altro aspetto caratteristico dei modelli MDP è la funzione di ricompensa.
Cos'è la funzione ricompensa?
Markov attribuisce delle ricompense positive e negative a ogni azione:
- La ricompensa positiva è associata al raggiungimento dell'obiettivo finale.
Esempio. Se l'agente razionale deve spostarsi dal punto X al punto Z, quando raggiunge il punto Z ( obiettivo ) gli viene assegnata una ricompensa +1.
- La ricompensa negativa ( penalità ) è la perdita di utilità o risorse conseguente a ogni decisione o allo scorrere del tempo. E' anche detta costo della decisione.
Esempio. L'obiettivo Z può essere raggiunto in poche o molte mosse. A parità di efficacia, è evidente che sia meglio raggiungerlo prima possibile, per risparmiare tempo e risorse. Per stimolare l'efficienza Markov associa a ogni decisione una penalità ( es. -0.01 ).
La somma algebrica delle ricompense R ottenute nel processo decisionale misura l'utilità delle decisioni.

In questo caso ho utilizzato il metodo delle ricompense additive.
E' quello più semplice perché la ricompensa in ogni singolo stato R(s) è indipendente dal tempo e dalla posizione nella sequenza degli stati.
Esempio. Data una sequenza di tre stati, la ricompensa dello stato R(s2) ha lo stesso valore sia se lo stato s2 si trova al secondo posto che al terzo.
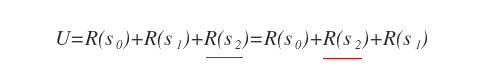
Pertanto, se le ricompense sono additive allora le preferenze sono stazionarie, perché l'utilità U della sequenza non cambia modificando l'ordine degli stati.
In alternativa, posso usare il metodo delle ricompense scontate.
Ogni ricompensa R viene moltiplicata per un fattore di sconto γ compreso tra zero e uno, elevato alla posizione dello stato nella sequenza decisionale.

In questo caso, la posizione dello stato nella sequenza decisionale ne modifica la ricompensa.
Esempio. Se il fattore di sconto è inferiore a 1, ad esempio y=0.5, le ricompense immediate sono più importanti delle ricompense future.
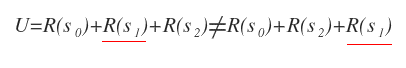
Pertanto, se le ricompense sono scontate, le preferenze non sono stazionarie perché l'utilità della sequenza cambia modificando l'ordine degli stati.
A cosa serve la funzione di ricompensa?
La funzione di ricompensa svolge due funzionalità:
- stimola l'efficienza della decisioni
- determina il grado di avversione al rischio dell'agente
Esempio. Se il costo di ogni decisione è basso, l'agente è maggiormente spinto a prendere la strada più lunga ma più sicura. Viceversa, se il costo di ogni decisione è alto, per raggiungere prima l'obiettivo finale l'agente è disposto a rischiare di più.
Un'altra via alternativa è quella dell'algoritmo con ricompensa media.
Un esempio pratico
Facciamo un esempio pratico, nella seguente mappa l'agente si trova alle coordinate A2.
L'obiettivo è raggiungere la casella C2 ( es. traguardo ) dove l'agente ottiene un premio +1 di utilità.
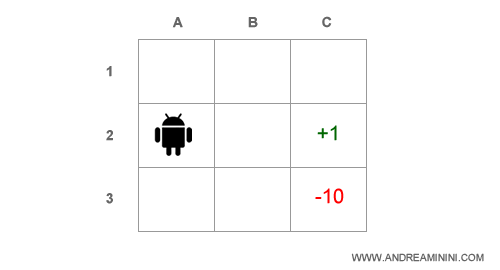
Deve anche evitare di passare per la casella C3 ( es. fossa ) dove subirebbe una penalità pari a -10.
Ogni passo costa all'agente una perdita di -0.1 di utilità.
Nota. Per ipotesi, si tratta di un ambiente chiuso, una matrice 3x3, e l'agente conosce la mappa ( informazione perfetta ). Sa dove si trova e sa dove deve andare.
Il caso di un modello deterministico ( certezza )
In un modello deterministico la scelta sarebbe facile, l'agente compie due decisioni in sequenza:
- Si sposta da A2 a B2 ( costo -0.1 )
- Si sposta da B2 a C2 ( costo -0.1 )
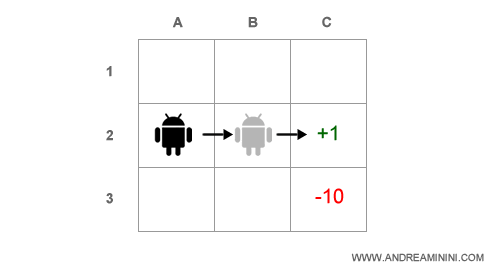
Complessivamente, il costo del cammino è di -0.2.
Pertanto, l'utilità netta dell'agente è 0.8 ossia +1-0.1-0.1.
Il caso di un modello probabilistico ( incertezza )
Nel modello probabilistico ogni decisione ha un margine di errore.
Quando l'agente decide di spostarsi, nel 90% dei casi si sposta effettivamente nella casella di destinazione.
Nel restante 10% potrebbe deviare a destra o a sinistra.
Esempio. Un colpo di vento improvviso sposta il drone mentre si sta muovendo. In questo caso, l'agente non raggiunge la casella desiderata, bensì la casella vicina.
Nella prima mossa l'agente razionale si sposta da A2 a B2.
La probabilità di raggiungere la casella B2 è del 90% mentre il costo della decisione è -0.1.
Fin qui non cambia nulla.
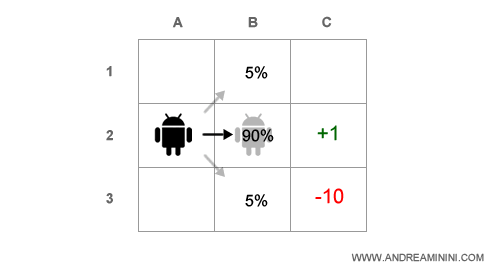
Nota. Per ipotesi l'agente, in questo esempio l'agente si sposta effettivamente nella casella B2. Tuttavia, va sottolineato che anche se capitasse per caso in B1 o B3 non subirebbe alcun danno, né rallentamento.
Nella seconda mossa l'agente si trova in B2 e dovrebbe spostarsi in C2.
Tuttavia, in questo caso deve considerare anche il rischio di deviare a causa di un colpo di vento e cadere in C3 ( fossa ).
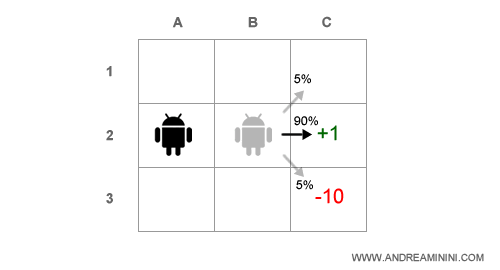
L'agente analizza i rischi e l'utilità attesa di tutte le azioni possibili per avvicinarsi a C2 da B2.
In particolar modo, l'agente confronta due percorsi alternativi:
- Primo percorso. Da B2 a C2 ( 1 mossa )
- Secondo percorso. Da B2 a C1, da C1 a C2 ( 2 mosse )

Il percorso più lungo B2-C1-C3 ha un'utilità attesa leggermente più alta ( 0.76 ) rispetto al percorso diretto B2-C2 ( 0.755 ).
Quindi, all'agente razionale conviene stare alla larga da C3 ( la fossa ) e scegliere la strada più lunga ma più sicura.

Nota. Se il costo del cammino fosse più alto, all'agente converrebbe rischiare il passaggio diretto da B2 a C2. Ad esempio, se il costo della decisione fosse -0.2 anziché -0.1, la decisione B2-C2 avrebbe un'utilità attesa pari a 0.66 mentre la decisione B2-C1-C2 soltanto 0.57. In questo caso all'agente conviene rischiare.
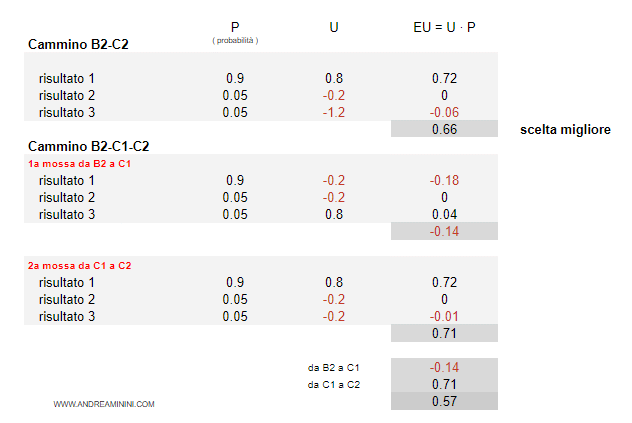
Per questa ragione la configurazione dei premi e delle penalità ( ricompense ) in un processo decisionale markoviano permette di definire l'approccio al rischio dell'agente.
La politica nei modelli MDP
In un modello decisionale di Markov, a ogni stato (s) potenzialmente raggiungibile dall'agente è associata un'azione raccomandata (a).
Questa soluzione è detta politica ( π ).
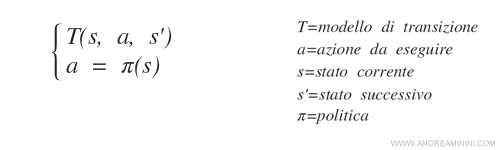
Se la politica fornisce la più alta utilità attesa tra le mosse possibili, è detta politica ottimale ( π* ).
In questo modo l'agente non deve mantenere in memoria le sue scelte precedenti.
Per prendere una decisione deve soltanto eseguire la politica associata allo stato corrente π(s).
Esempio. La politica π(B2) è spostarsi nella casella C2. La politica ottimale π(C2) è spostarsi nella casella C2. Entrambe le politiche sono calcolate considerando l'utilità attesa e le ricompense, perché l'agente non sta lavorando in un ambiente deterministico bensì stocastico.

Come trovare la politica ottimale
Una politica ottimale ( π* ) è la sequenza di azioni che consente all'agente di raggiungere l'obiettivo con la massima utilità attesa. E' la strada migliore tra tutte.
Per trovarla l'agente deve saper pianificare le mosse su più turni in anticipo.
Nota. Non basta calcolare la mossa migliore nel turno successivo perché l'agente rischia di diventare miope. Ad esempio, la prima mossa potrebbe sembrare la migliore ma poi condurre l'agente in un vicolo cieco. Soltanto una visione generale consente all'agente di individuare fin dall'inizio il percorso migliore.
Esistono diverse tecniche di pianificazione per trovare la politica ottimale.
Ad esempio l'algoritmo di iterazione dei valori e l'algoritmo di iterazione delle politiche.
Un altro algoritmo si chiama iterazione asincrona delle politiche.
Nota. L'algoritmo di iterazione asincrona alterna l'iterazione dei valori e l'iterazione delle politiche a seconda delle circostanze in base a una funzione euristica.
L'orizzonte temporale del problema
Il tempo necessario per risolvere il problema influisce sulle decisioni dell'agente.
L'orizzonte temporale può essere:
- Finito. L'agente deve raggiungere l'obiettivo entro un tempo T prefissato ( o N mosse ). La soluzione deve essere trovata con una sequenza di azioni entro il tempo massimo, altrimenti è inutile. In questo caso la politica non è stazionaria perché le decisioni ottimali in ogni stato variano a seconda del tempo.
- Infinito. L'agente non ha limiti di tempo per raggiungere l'obiettivo oppure il tempo massimo T è molto ampio. In questo caso la politica è stazionaria perchè non cambia con il tempo. Le azioni dipendono soltanto dallo stato corrente.
Esempio. Se l'agente deve raggiungere l'obiettivo in due mosse (N=2) e dopo la prima mossa si trova nello stato B2, nella seconda mossa deve necessariamente rischiare il passaggio diretto da B2 a C2 ( traguardo ). Anche se questo comporta il rischio di cadere nella casella C3 ( fossa ).

Se prendesse la strada più lunga e sicura da B2 a C1, nella migliore delle ipotesi raggiungerebbe la casella C2 ( obiettivo ) in tre mosse, oltre il tempo massimo consentito. Quindi, la politica sarebbe inutile.
MDP parzialmente osservabili ( POMDP )
I processi decisionali di Markov ( MDP ) in condizioni parzialmente osservabili ( PO ) sono detti problemi ( POMDP ).
In un problema POMDP l'agente non sa in quale stato si trova.
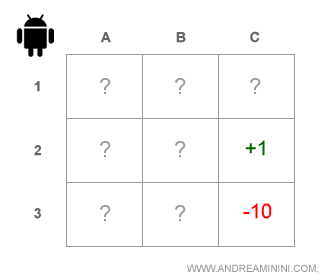
Esempio. Nel problema POMDP l'agente non sa di trovarsi nella casella A2. Non sapendo dove si trova ( stato reale corrente ) non riesce a decidere quali azioni compiere per raggiungere la casella obiettivo C2.
Quindi non può ottenere la migliore politica possibile a partire dallo stato reale corrente.
Sono problemi decisamente più difficili da risolvere rispetto agli MDP.
