L'algoritmo di Viterbi
L'algoritmo di Viterbi permette di trovare la sequenza più probabile degli eventi in un processo markoviano.
Un esempio pratico
Un medico deve capire se una persona è stata contagiata da una febbre tropicale dopo una vacanza in un paese straniero.
Il paziente dichiara di sentirsi bene al suo rientro ma la malattia potrebbe essere in incubazione.
In questo caso la malattia ( febbre ) è la variabile nascosta X del problema.
Nota. Il medico non può sapere se la persona ha la febbre oppure no fino al termine del periodo di incubazione.
Il medico sa che soltanto il 40% delle persone viene contagiato dal virus, il restante 60% è sano.

Tuttavia, si tratta di una stima generale.
Il medico sa anche che la probabilità varia a seconda se si manifesta o meno la febbre nei giorni successivi.
- Al 70% il paziente è sano se nei giorni successivi sta bene.
- La probabilità che sia sano scende al 40% se si manifesta la febbre.
Questo permette di costruire il modello di transizione degli stati nel tempo.
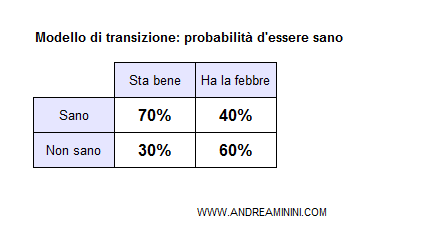
Nota. Anche se nei giorni successivi il paziente ha la febbre, nel 40% dei casi potrebbe trattarsi soltanto di un'influenza passeggera e il paziente è sano. Non ha contratto la malattia tropicale. Nel restante 60% è invece contagiato.
Per stimare meglio il rischio, il medico prende in considerazione anche i sintomi del paziente ( vertigini, brividi, normale ) nei giorni successivi.

Nota. Se il paziente sta bene ma ha le vertigini, la probabilità che sia sano scende al 10%. Se sta bene e ha i brividi la probabilità d'essere sano è del 40%. Se non ha né brividi, né vertigini, al 50% è sano. Se il paziente ha la febbre e le vertigini la probabilità d'essere sano è del 60%. Se ha la febbre e i brividi la probabilità che sia sano è del 30%. Se non ha né brividi, né vertigini al 10% è sano.
I sintomi del paziente sono le variabili di prova e permettono di costruire il modello sensoriale del problema.
A questo punto si può calcolare l'algoritmo di Viterbi.
Primo giorno
Il medico visita la persona nel primo giorno e il paziente è normale, non ha sintomi.
Al 60% è sano (S) e al 40% è stato contagiato dalla febbre (F).

Poiché non ha sintomi ( normale ) la probabilità congiunta è 0.3 ( sta bene ) e 0.04 ( ha la febbre ).
Pertanto, nel primo giorno il cammino più probabile è S ( sta bene ).
Secondo giorno
Il medico visita la persona nel secondo giorno e il paziente ha i brividi.
L'algoritmo di Viterbi estrapola i seguenti risultati:

La sequenza più probabile è la prima ( 0.084 ).
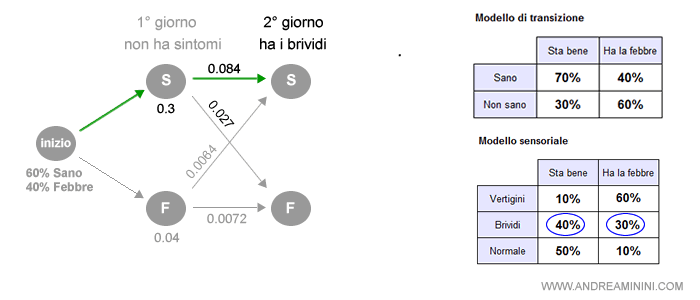
Pertanto, è ancora probabile che il paziente sia sano.
Terzo giorno
Il medico visita la persona nel terzo giorno e il paziente ha le vertigini.
L'algoritmo di Viterbi estrapola i seguenti risultati:

La sequenza più probabile è la seconda ( 0.015 ).
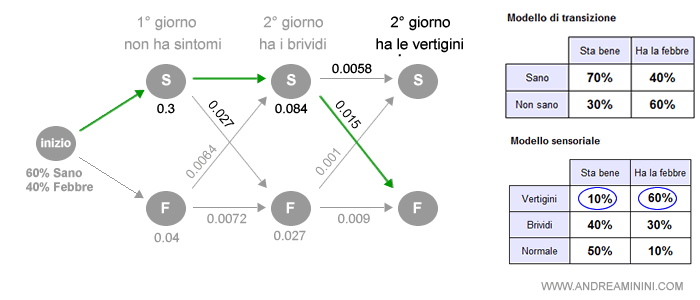
Pertanto, è probabile che il malato sia contagiato dalla febbre tropicale.
La probabilità normalizzata
Una volta ottenuta la sequenza più probabile degli stati, si può calcolare la probabilità normalizzata.
Cos'è la probabilità normalizzata? Si ottiene facendo in modo che la somma della probabilità dell'evento e della probabilità inversa sia uguale a 1 ossia al 100%.
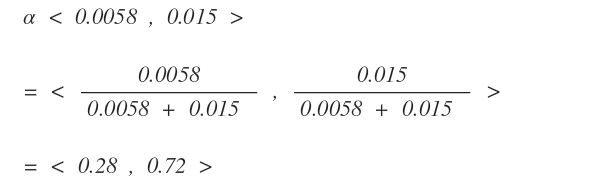
La probabilità normalizzata del paziente è < 0.28, 0.72>.
Il paziente è al 28% sano e al 72% è malato.
Nota. Pur non potendo appurare lo stato di malattia della persona durante il periodo di incubazione, osservando i sintomi il medico può stabilire che probabilmente il paziente è stato contagiato dalla febbre durante la sua permanenza all'estero.
Questo è un esempio di funzionamento dell'algoritmo di Viterbi.
