La sequenza pił probabile
Negli algoritmi predittivi è necessario elaborare una previsione sugli stati futuri del sistema. Per farlo si ricorre alle catene di Markov e all'individuazione della sequenza degli stati ( cammino o path ) più probabile.
Nota. In una catena di Markov il valore di ogni stato ( nodo ) è influenzato dai nodi precedenti.
Alla base di questa soluzione c'è la seguente ipotesi fondante: il cammino più probabile che porta a uno stato Xt+1 ha una relazione con i cammini più probabile che portano allo stato precedente Xt.
La rappresentazione della catena in un grafo
Per studiare la sequenze dei valori più probabili di una particolare variabile, si utilizza la rappresentazione grafica degli stati temporali tramite un grafo orientato.
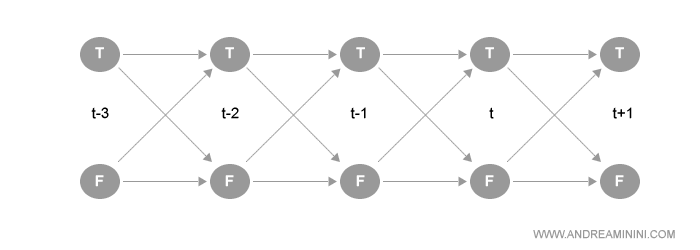
In un grafo i nodi identificano gli stati temporali, ossia i valori registrati dalla variabile, mentre gli archi le relazioni tra uno stato temporale e il successivo.
Nel precedente grafico ho utilizzato una semplice variabile booleana che può assumere soltanto i valori True ( T ) o False ( F ).
Come trovare la sequenza più probabile
In questo caso non si può usare l'algoritmo di smoothing ( regolarizzazione ) perché si limita a calcolare la probabilità di un singolo stato.
Per trovare la sequenza più probabile occorre lavorare sulle probabilità congiunte di tutti i passi temporali ( nodi ) del cammino.
Cos'è una probabilità congiunta? Una probabilità congiunta è il prodotto delle probabilità dei singoli stati del cammino posti in ordine sequenziale tra loro. Ad esempio, qual è la probabilità che piova ( P1 ) e ci sia vento ( P2 ) nello stesso giorno.
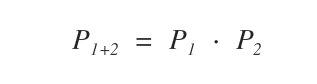
Un algoritmo utile a questo scopo è l'algoritmo di Viterbi, ideato da Andrew Viterbi nel 1962 per trovare la sequenza degli eventi più probabili in un processo markoviano.
Come funziona l'algoritmo di Viterbi
Facciamo un esempio pratico, il cammino che porta allo stato True nell'istante t include anche lo stato nell'istante precedente t-1.
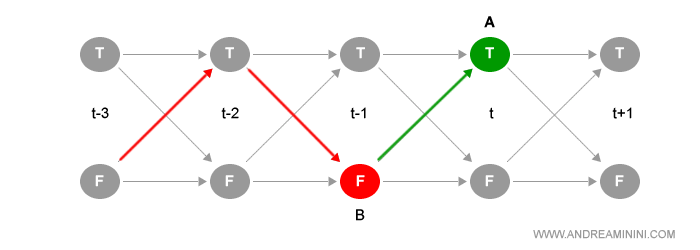
Pertanto, il cammino che porta al nodo A include anche il cammino più probabile che porta allo stato B. E così via.
La formula generale dell'algoritmo è la seguente:
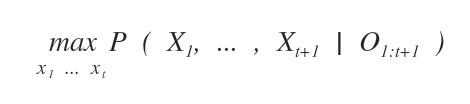
Data una serie di osservazioni della variabile di prova O dall'istante 1 a t+1, la probabilità congiunta del cammino che conduce all'evento Xt+1 è quella che massimizza il cammino fino al nodo precedente Xt.
Cos'è la variabile di prova?. La variabile di prova O è quella osservata che ci permette di stimare la variabile incognita X. Ad esempio, se in un ufficio sotterraneo entra una persona con l'ombrello (O=true) è probabile che fuori piova (X). Noi non possiamo vedere se fuori piove oppure no (X) ma vediamo l'ombrello (O). Quindi possiamo calcolare una probabilità di pioggia ricorrendo a un modello sensoriale e di transizione tramite la tecnica del filtraggio ( o monitoring ).
Ipotizziamo di voler calcolare la probabilità condizionata dello stato Xt+1 in base alla variabile di prova Ot+1.
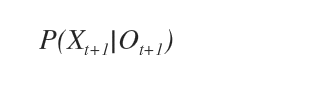
Alla probabilità condizionata possiamo applicare il teorema di Bayes.
Nota. Secondo la regola di Bayes una probabilità condizionata P(A|B) può essere scomposta in α P(B|A)P(A). Dove alfa (α) è un parametro moltiplicativo per ottenere la somma delle probabilità pari a 1.
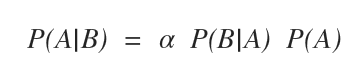
Possiamo riscrivere la probabilità condizionata nel seguente modo:
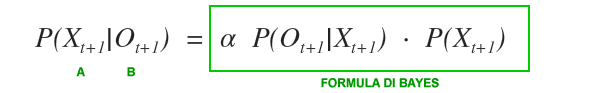
Sappiamo che la probabilità del nodo Xt+1 è uguale alla probabilità di transizione dallo stato precedente P(Xt+1|Xt) moltiplicata per la probabilità congiunta del cammino fino a Xt.
Pertanto, possiamo riscrivere la formula nel seguente modo:

A questo punto possiamo calcolare la massima probabilità condizionata del nodo Xt+1 tenendo conto sia della transizione con lo stato precedente P(Xt+1|Xt) e sia della massima probabilità congiunta ( sequenza più probabile ) fino al nodo precedente Xt.
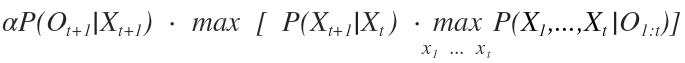
L'algoritmo di Viterbi procede con una ricorsione in avanti a partire dal primo nodo fino all'ultimo.
In ogni passo calcola la probabilità P(Xt+1|Xt) usando la formula precedente.
In questo modo l'algoritmo seleziona la sequenza di stati più probabile.
Un esempio pratico
A partire dal primo nodo a sinistra, l'algoritmo calcola le probabilità del percorso tra i primi due nodi.
Tra i due prevale il nodo S con una probabilità di 0,3 contro 0,004.
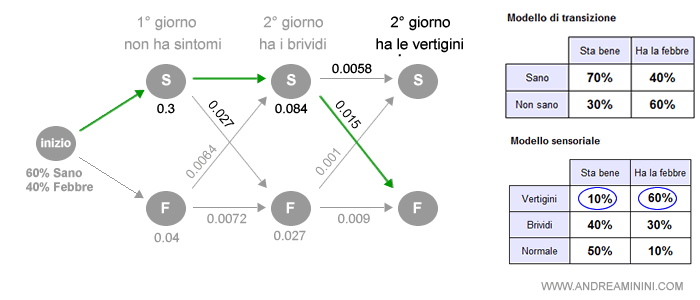
Nel secondo giorno il modello calcola le sequenze possibili considerando le probabilità del modello di transizione e sensoriale e le probabilità dei percorsi passati.
Prevale il nodo S con una probabilità congiunta pari a 0,084. E così via.
Per vedere l'esempio completo con tutti i passaggi in dettaglio.
Nota. Dopo ogni passaggio l'algoritmo memorizza le seguenze che hanno portato agli ultimi nodi. Pertanto, l'algoritmo di Viterbi ha una complessità lineare sia nell'utilizzo dello spazio di memoria che nel tempo di esecuzione.
