Solutions to Optimization Problems
In linear programming, the solutions of an optimization problem form a set known as the feasible region.
The feasible region is a polyhedron P in space.
If the objective is to minimize costs, we write:
$$ \min_{ \forall x \in P} f(x) = c^T x $$
Within the feasible region P, there may exist an optimal solution x*.
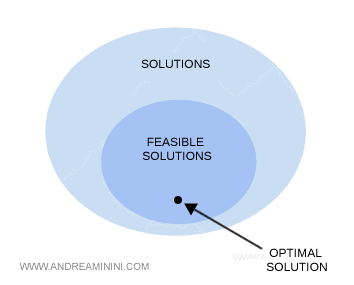
What do we mean by an optimal solution?
An optimal solution to the problem is a point x* in P such that
$$ c^Tx* \le c^Tx \:\:\:\text{ for every } x \in P$$
A practical example
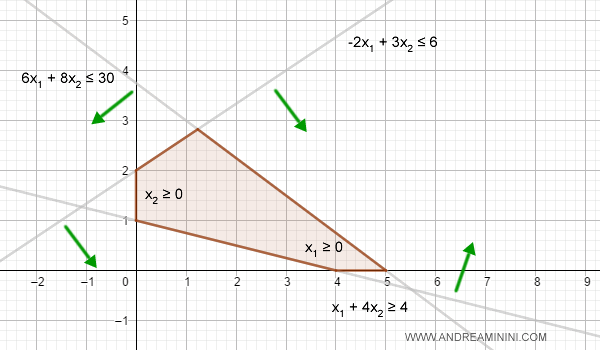
Consider an optimization problem with the following objective function:
$$ \min z(x) = x_1 + 2x_2 $$
subject to the constraints:
$$ \begin{cases} 6x_1+8x_2 \le 30 \\ -2x_1+3x_2 \le 6 \\ x_1+4x_2 \ge 4 \\ x_1 \ge 0 \\ x_2 \ge 0 \end{cases} $$
We can represent the optimization model on the Cartesian plane.
This allows us to visualize the feasible region geometrically.
Note. If the feasible region does not exist, the solution set is empty ( P=ø ) and the problem is infeasible. In that case we write z*=+∞.
How do we find the solution?
We can either solve the linear system algebraically or determine the solution graphically.
On the diagram, we add the cost gradient.
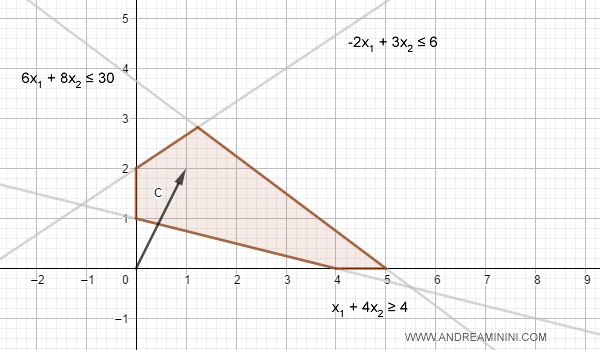
The gradient is simply the cost vector cT: $$ c = \begin{pmatrix} 1 \\ 2 \end{pmatrix} \\ c^T = ( 1 , 2 ) $$
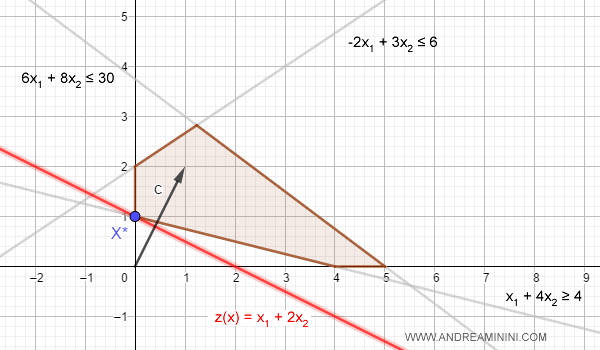
The solution is the point x* in the polyhedron P that yields the lowest value of z(x), lying on the line perpendicular to the gradient.
Note. If the feasible region exists but no optimal point x* can be identified, the problem is unbounded below. For every feasible solution x∈P there is always another with a smaller objective value. In this case, no optimal solution exists and we write z*=-∞.
The optimization problem in standard form
- An optimization problem is in standard form
- if the objective function is a minimization function.
- if the solution set P is a non-empty polyhedron in standard form.
Example
The system above
$$ \begin{cases} \min z(x) = x_1 + 2x_2 \\ \\ 6x_1+8x_2 \le 30 \\ -2x_1+3x_2 \le 6 \\ x_1+4x_2 \ge 4 \\ \\ x_1 , x_2 \ge 0 \end{cases} $$
in standard form becomes
$$ \begin{cases} \min z(x) = x_1 + 2x_2 \\ \\ 6x_1+8x_2 +x_3 = 30 \\ -2x_1+3x_2 +x_4 = 6 \\ x_1+4x_2 -x_5 = 4 \\ \\ x_1, x_2, x_3,x_4,x_5 \ge 0 \end{cases} $$
Why use standard form?
Standard form introduces useful geometric properties that make it easier to analyze and solve optimization problems.
-
If a direction d of the polyhedron satisfies cTd < 0, the problem is unbounded below.
A problem is unbounded below if it admits no optimal solution, since every feasible solution can always be improved upon. Here is a practical example.
Basic solutions and vertices of the polyhedron
From a geometric standpoint, solutions occur at the vertices of the polyhedron. These are called basic solutions.
Not every basic solution, however, is feasible.
Among them, we must identify the basic feasible solutions (BFS) and discard those that are not.
