Algoritmo di scomposizione in fattori primi

Questo algoritmo scompone un numero nei suoi fattori primi.

L'algoritmo chiama la funzione primo(n) per verificare se un numero è un numero primo. E' descritta in dettaglio in un altro appunto ( clicca qui ).

Come funziona l'algoritmo

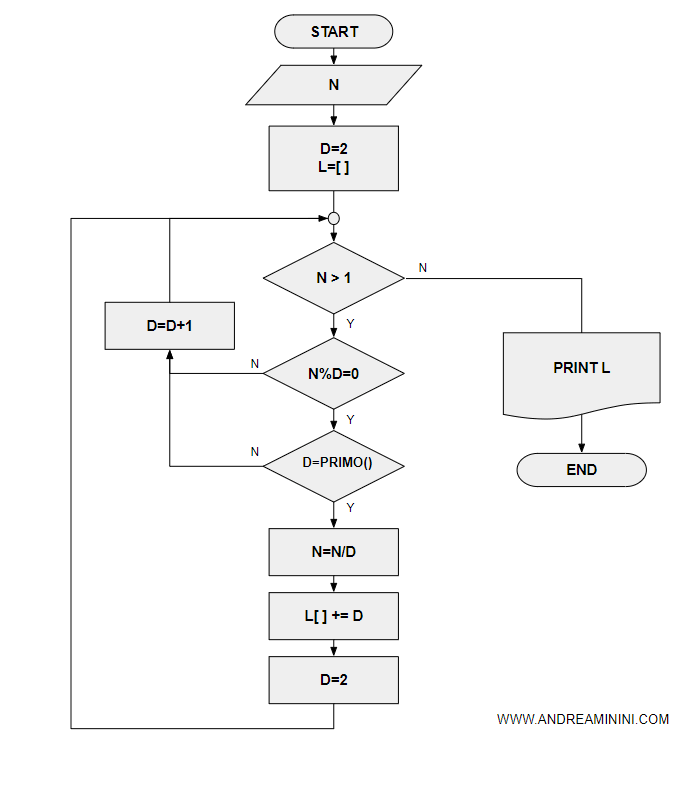
L'algoritmo cerca il numero primo (i) più basso in grado di dividere il numero (n) senza resto.

Quando lo trova, divide il numero (n) per (i)

Poi azzera il numero i.

Il processo termina quando il numero n diventa uguale a 1.

Il diagramma a blocchi

L'algoritmo della scomposizione è rappresentabile tramite un flow chart.

Un esempio pratico

Devo analizzare il numero 20.

Provo a dividerlo per 2 e controllo se la divisione restituisce un resto.

$$ 20\%2=0 $$

Si tratta di una divisione senza resto e il divisore (d=2) è un numero primo.

Quindi, aggiorno il valore di n

$$ n=\frac{20}{2}=10 $$

Aggiungo 2 tra i divisori del numero.

$$ lista=[2] $$

Poi inizializzo a 2 il valore del divisore (d).

Ora provo a dividere 10 per due.

$$ 10\%2=0 $$

E' un'altra divisione senza resto e il divisore (d=2) è un numero primo.

Quindi, aggiorno il valore di n

$$ n=\frac{10}{2}=5 $$

Aggiungo il divisore (2) alla lista dei fattori.

$$ lista=[2,2] $$

Poi reinizializzo a due la variabile del divisore (d=2).

Ora provo a dividere 5 per 2.

$$ 5\%2=1 $$

Non è una divisione senza resto, quindi passo al divisore successivo (d=d+1).

Provo a dividere 5 per 3.

$$ 5\%3=2 $$

Anche in questo caso c'è resto e passo al divisore successivo (d=d+1).

Provo a dividere 5 per 4.

$$ 5\%4=1 $$

Non è una divisione per intero e passo al divisore successivo (d=d+1).

Ora provo a dividere 5 per 5.

$$ 5\%5=0 $$

E' una divisione senza resto e il divisore (5) è un numero primo.

Aggiungo 5 tra i divisori.

$$ lista=[2,2,5] $$

Poi aggiorno il valore del numero n

$$ n=\frac{5}{5}=1 $$

A questo punto il numero (n) è diventato inferiore a 2 e l'algoritmo finisce qui.

L'output del programma

La lista contiene i seguenti valori:

$$ [2,2,5] $$

ossia

$$ 2 \cdot 2 \cdot 5 $$

$$ 2^2 \cdot 5 $$

Ho così scomposto il numero in fattori primi.

Lo pseudocodice

1. class scomponi() {
2. i=1
3. lista=[]
4. while (n>1)
5. #se i è un numero primo e divide il numero n
6. if i=primo(i) and n%i=0
7. #dividi il numero
8. n=n/i
9. #aggiungi i alla lista
10. lista+=i
11. i=i+1
12. }