L'algoritmo merge sort
L'algoritmo merge sort è un algoritmo di ordinamento basato sulla ricorsione e sull'approccio divide et impera.
Come funziona. L'array viene suddiviso in subarray di dimensioni man mano più piccole. Successivamente i sottoarray sono fusi (merge) tra loro fino a ricostruire l'array iniziale in ordine crescente.
Come funziona merge sort
L'array iniziale viene spezzato in due suddiviso in subarray.
Ad esempio, l'array = [2,5,1,1,6,7,3] viene diviso in due subarray L=[2,5,1,1] e R=[6,7,3]
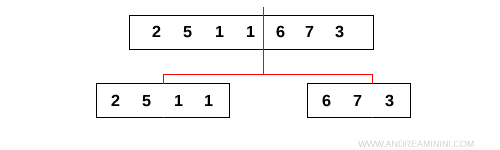
A loro volta anche i subarray sono spezzati e divisi in altri subarray più piccoli.
Il subarray [2,5,1,1] viene suddiviso in due subarray L=[2,5] e R=[1,1]
Allo stesso modo il subarray [6,7,3] viene suddiviso in due subarray L=[6,7] e R=[3]
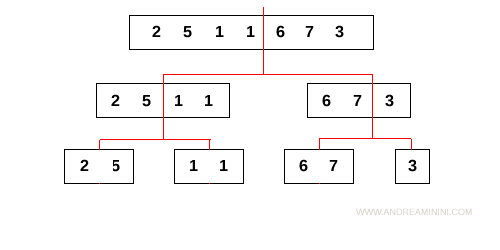
La suddivisione termina quando l'algoritmo non può ulteriormente spezzare in due i subarray.
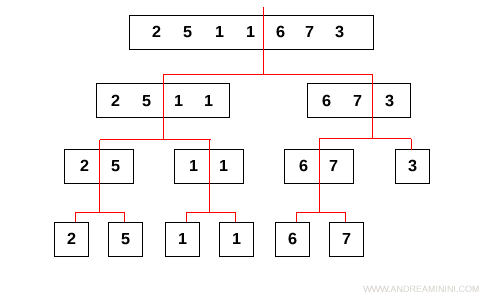
A questo punto l'algoritmo confronta i subarray più piccoli.
Ad esempio, confronta i subarray L=[2] e R=[5].
Essendo 2<5 lascia il subarray immutato perché il subarray [2,5] è già ordinato in modo crescente.
![il subarray [2,5] è ordinato](https://www.andreaminini.com/data/andreaminini/nc-algoritmo-merge-sort-spiegazione-funzionamento-am-3.gif)
Poi confronta i subarray L=[1] e R=[1]
I due elementi sono uguali, quindi lascia il subarray [1,1] immutato.
![il subarray [1,1] è ordinato](https://www.andreaminini.com/data/andreaminini/nc-algoritmo-merge-sort-spiegazione-funzionamento-am-4.gif)
Infine confronta i subarray L=[6] e R=[7]
Essendo 6 inferiore di 7, lascia il subarray immutato.
![il subarray [6,7] è già ordinato](https://www.andreaminini.com/data/andreaminini/nc-algoritmo-merge-sort-spiegazione-funzionamento-am-5.gif)
L'algoritmo passa a confrontare i subarray del livello superiore.
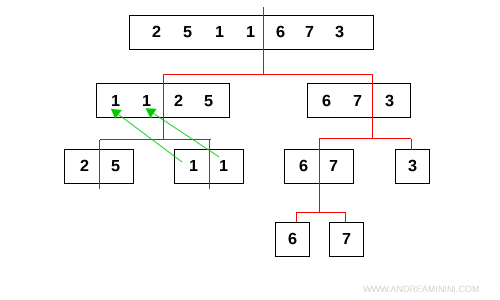
Confronta i subarray [2,5] e [1,1] scegliendo gli elementi in ordine crescente: 1, 1, 2, 5.
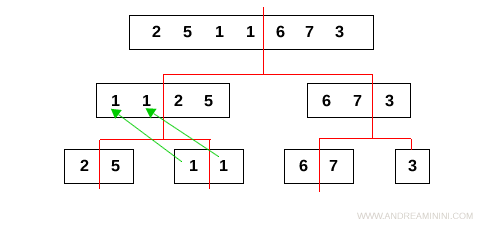
Nota. L'algoritmo sceglie gli elementi tra i subarray [2,5] e [1,1] come se fossero quattro carte sul tavolo. Prima prende gli elementi 1 e 1 perché sono più bassi. Poi gli elementi 2,5.
Poi confronta i subarray [6,7] e [3] scegliendo gli elementi in ordine crescente: 3, 6, 7.
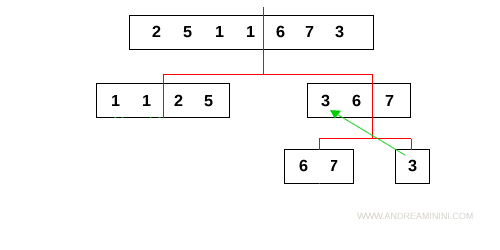
Ora l'algoritmo confronta i subarray [1,1,2,5] e [3,6,7] scegliendo gli elementi dal più piccolo al più alto.
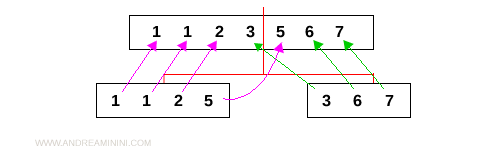
Il risultato finale è l'array ordinato in modo crescente.
Nota. In questa spiegazione ho usato una logica incrementale perché più semplice e intuitiva. Nella realtà, per risparmiare spazio di memoria è preferibile eseguire l'algoritmo merge sort tramite ricorsioni. Cosa cambia? Le ricorsioni ordinano in profondità prima il ramo sinistro dell'albero logico.
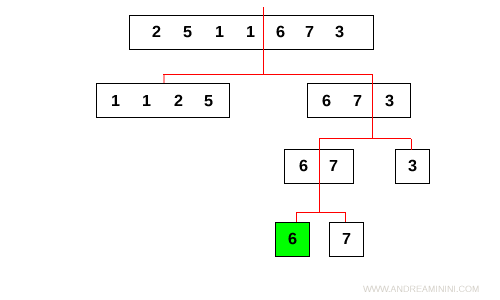
Poi ordina in profondità il ramo destro.
![l'algoritmo confronta gli array [6,7] e [3]](https://www.andreaminini.com/data/andreaminini/nc-algoritmo-mergesort-mergesort-am-9.gif)
Il risultato finale è sempre lo stesso.
L'algoritmo merge sort in Python
Un esempio pratico di sviluppo dell'algoritmo merge sort usando il linguaggio Python
L'algoritmo è suddiviso in tre moduli
- Un programma principale
In questo programma definisco l'array da ordinare e chiamo la funzione mergesort().
- Funzione mergeSort(array,l,r)
Questa funzione divide l'array in due sottoarray. Richiama ricorsivamente se stessa fino ad arrivare a più subarray di dimensioni più piccole. Infine, richiama la funzione merge() per fondere i subarray ordinati fra loro.
- Funzione merge(array, l,m,r)
Questa funzione fonde due parti dell'array ordinate tra loro. La prima parte include gli elementi compresi tra gli indici (l,m). La seconda parte, invece, gli elementi tra gli indici (m+1,r). Al termine dell'esecuzione la funzione restituisce l'array con gli elementi nell'intervallo (l,r) ordinati in modo crescente.
Come funziona l'algoritmo
Inizialmente definisco un array da ordinare e conto il numero degli elemento del vettore.
Il programma principale chiama la funzione mergeSort() passandogli come parametri
- il nome dell'array
- l'indice iniziale dell'array (0)
- l'indice finale dell'array (6)
Nota. Il passaggio di un array come parametro avviene per riferimento. Questo vuol dire che la funzione riceve l'indirizzo di memoria dove si trova l'array e non una copia degli array. Pertanto, ogni modifica effettuata dalla funzione modifica effettivamente l'array. Viceversa, il passaggio delle variabili avviene per valore. In questo caso la funzione riceve una copia del valore della variabile (n=6) e non può modificare il valore originale.
La funzione mergeSort(array,l,r) riceve il riferimento dell'array arr=[2,5,1,1,6.7.3] da ordinare, la posizione del primo elemento l=0 e quella dell'ultimo elemento r=6 nell'indice dell'array.
La funzione mergeSort trova l'elemento centrale dell'array (m) e richiama se stessa in ricorsione due volte
- nella prima ricorsione passa la posizione indice della prima metà dell'array da l=0 a m=3 (subarray della prima metà)
- nella seconda ricorsione passa la posizione indice della seconda metà dell'array da m=4 a r=6 (subarray della seconda metà)
A ogni ricorsione l'algoritmo passa un numero minore di elementi.
La ricorsione termina quando i due subarray hanno ciascuno un elemento.
A questo punto la funzione mergeSort() chiama la funzione merge(arr,l,m,r) per ordinare e fondere i due subarray.
La funzione merge() confronta i due subarray e li ordina scegliendo man mano l'elemento minore.
La funzione merge confronta dapprima gli elementi unitari del primo subarray L=2 e R=5 poi L=1 e R=1
Li confronta e sceglie l'elemento minore. In questo caso gli elementi sono già ordinati.
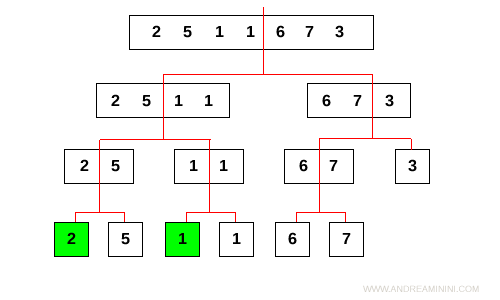
Successivamente l'algoritmo confronta i subarray L=[2,5] e R=[1,1] scegliendo man mano gli elementi minori.
A questo punto l'algoritmo avvia e chiude le ricorsioni sul secondo subarray.
Dapprima confronta gli elementi L=6 e R=7 scegliendo quello minore.
Poi confronta i subarray L=[6,7] e R=[3]
Infine, l'array chiude la ricorsione confrontando il primo subarray L=[1,1,2,5] e il secondo subarray R=[3,6,7]
Entrambi i subarray sono ordinati grazie alle precedenti ricorsioni.
Il risultato finale è l'array ordinato in modo crescente.
E così via.
