L'algoritmo di Dijkstra
L'algoritmo di Dijkstra si usa per trovare il cammino ottimale da un nodo iniziale a un nodo finale in un digrafo ( grafo orientato ) aciclico e con costi non negativi.
Si tratta di un algoritmo ad assegnazione di etichetta, perché i nodi una volta analizzati ed etichettati, non possono essere più modificati.
Questa caratteristica riduce la complessità computazionale dell'algoritmo al numero N dei nodi del digrafo.
Nota. Il numero di iterazioni dell'algoritmo non può superare il numero dei nodi presenti nel grafo orientato.
Come funziona
L'algoritmo prende in input
- un digrafo D=(N,A) dove N è il vettore dei nodi e A è il vettore degli archi.
- un vettore c(i,j) con i costi degli archi
- un nodo s iniziale
Al termine dell'elaborazione l'algoritmo fornisce in output
- un vettore delle etichette (d) con le distanze/costi minimi dei percorsi dal nodo iniziale s verso qualsiasi altro nodo del digrafo
- un vettore (pred) in cui è indicato il migliore predecessore di ogni nodo.
L'elaborazione si svolge in due fasi
1] Inizializzazione
Nella fase iniziale inizializzo le variabili e i vettori nel seguente modo:
| d[s]=0 | distanza nodo iniziale=0 |
| d[i]=∞ | distanza iniziale di ogni nodo diverso da s |
| pred[i]=i | ogni nodo ha predecessore se stesso |
| L={s} | la lista dei nodi da analizzare contiene il nodo s |
| S={} | la lista dei nodi già analizzati/etichettati |
2] Iterazione
Nella fase successiva l'algoritmo analizza il grafo compiendo al massimo n iterazione. Dove n è il numero dei nodi presenti nel vettore N.
- Finché la lista dei nodi da visitare L non è vuota
- estrarre dalla lista L il nodo x con distanza più bassa
- eliminare il nodo x dalla lista L (nodi da analizzare)
- aggiungere il nodo x alla lista S (nodi analizzati)
- analizzare ogni nodo j adiacente di x se j non è in S (nodi analizzati)
- calcolare la distanza dei nodi adiacenti del nodo x d'[j]=d[x]+c(x,j)
- se ll costo d'[j]<d[j]
- aggiornare il vettore d[j]=d'[j]
- aggiornare il predecessore pred[j]=x
- aggiungere alla lista L il nodo adiacente j (se non presente)
Al termine dell'esecuzione l'algoritmo indica il costo minimo d[i] del percorso per raggiungere l'i-esimo nodo a partire dal nodo iniziale s.
Se un valore d[i] è infinito, vuol dire che l'i-esimo nodo non è raggiungibile da s.
Nota. L'insieme dei cammini orientati dal nodo s verso gli altri nodi del grafo crea un sottodigrafo di nodi raggiungibili detto arborescenza del digrafo.
Lo pseudocodice
Per programmare l'algoritmo di Dijkstra su un digrafo aciclico con costi non negativi, posso usare questa versione dell'algoritmo.
- d:=[]
- pred[s]:=s
- for each nodo ≠ s
- d[nodo]= +∞
- pred[nodo]=nodo
- S:=[]
- L:=[s]
- while L≠[]
- i=min(d[j]:j di L)
- S:=S∪{i}
- L:=L\{i}
- for each (i,j) di archi_in_uscita[i]≠s
- if d[j]>d[i]+c[i,j] then
- d[j]:=d[i]+c[i,j]
- pred[j]=i
- L=L∪(j)
Per capire lo pseudocodice è utile seguire l'esempio pratico.
Un esempio pratico
Per spiegare il funzionamento dell'algoritmo di Dikstra prendo come esempio un digrafo.
Il digrafo ha n=4 nodi e m=5 archi.
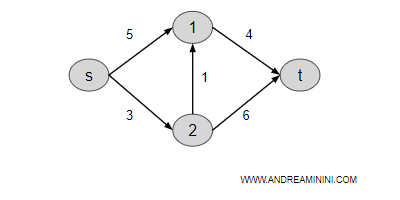
I costi sono tutti non negativi e non ci sono cicli.
La prima fase dell'algoritmo è l'inizializzazione.
La fase di inizializzazione
Creo due liste L e S
- L = lista dei nodi da analizzare
- S = lista dei nodi già visitati
Inizialmente la lista S è vuota mentre la lista L contiene il nodo iniziale s (start) del digrafo.
$$ L = \{s\} \\ S = \{\} $$
Creo il vettore dei costi del cammino d.
Questo vettore misura il costo minimo per raggiungere un nodo a partire dal nodo s.
Inizialmente tutti i costi sono uguali a +inf salvo il primo (s) che è uguale a s.
$$ d=[s, +∞, +∞, +∞ ] $$
Poi creo un vettore con i nodi precedenti migliori per ciascun nodo del digrafo.
Inizialmente, a ogni nodo è assegnato se stesso.
$$ pred=[s,1,2,t] $$
La fase di elaborazione
Iterazione 1
La fase di elaborazione comincia con l'estrazione di un nodo dalla lista L.
Il nodo (s) estratto viene tolto da L e inserito in S.
$$ L=\{\} \\ S=\{s\} $$
Si analizzano gli archi uscenti dal nodo appena estratto (s)
In questo caso il nodo s ha due archi uscenti che lo collegano ai nodi 1 e 2.
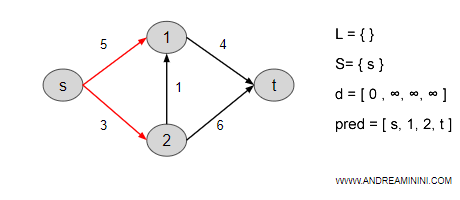
Calcolo i costi cumulati dei due archi
$$ d_s+c_{s1}=0+5=5 \\ d_s+c_{s2}=0+3=3 $$
Entrambi i costi comulati sono inferiori ai costi dei nodi 1 e 2 nel vettore d.
$$ d_s+c_s1= 5 < d_1 = ∞ \\ d_s+c_s2= 3 < d_2 = ∞ $$
Ecco l'esempio del calcolo dei costi cumulati d sul nodo 2.
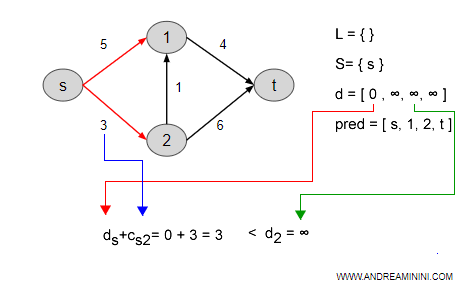
In questo caso posso aggiornare i vettori d, pred e inserire i due nodi 1 e 2 nella lista dei nodi da visitare.
Dopo la modifica i vettori d e pred sono i seguenti
$$ d = [ 0, 5, 3, ∞ ] \\ pred = [ s, s, s, t ] $$
Il vettore d= [ 0, 5, 3, ∞ ] equivale a d[s]=0, d[1]=5, d[2]=3, d[t]=∞.
Il vettore pred = [ s, s, s, t ] equivale a pred[s]=s, pred[1]=s, pred[2]=s, pred[t]=t.
Poi aggiungo i nodi 1 e 2 tra i nodi da visitare:
$$ L = \{ 1, 2 \} $$
I nodi adiacenti vanno aggiunti nella lista dei nodi da visitare soltanto se è stato aggiornato il costo cumulato d. In caso contrario, non vanno inseriti in L.
Iterazione 2
Nell'iterazione successiva ho due nodi nella lista L.
Il nodo 1 e il nodo 2.
$$ L = \{ 1, 2 \} $$
Devo estrarre il nodo che ha un costo di cammino minore.
$$ d = [ 0, 5, 3, ∞ ] $$
In questo caso d[1]=5 e d[2]=3.
Quindi, estraggo il nodo 2 da L e lo aggiungo alla lista dei nodi visitati S.
$$ L = \{ 1 \} \\ S=\{ s, 2 \} $$
Il nodo 2 ha due archi in uscita verso il nodo 1 e il nodo t.
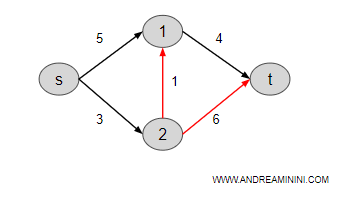
I costi verso i due nodi sono:
$$ d_2+c_{2,1}= 3+1 = 4 < d_1 = 5 \\ d_2+c_{2,t}= 3+6 = 9 < d_t = ∞ $$
Sono entrambi inferiori alle etichette temporanee dei nodi 1 e t nel vettore d.
$$ d = [ 0, 5, 3, ∞ ] $$
Quindi, aggiorno i vettori d e pred con i nuovi dati.
$$ d = [ 0, 4, 3, 9 ] \\ pred = [ s, 2, s, 2 ] $$
Poi aggiungo i nodi 1 e t alla lista dei nodi da visitare.
Il nodo 1 è già presente in L, quindi non lo riaggiungo.
$$ L = \{ 1, t \} \\ S=\{ s, 2 \} $$
Iterazione 3
Nell'iterazione successiva ho due nodi nella lista L.
Sono il nodo 1 e il nodo t.
$$ L = \{ 1, t \} $$
Il nodo 1 ha un costo di cammino d[1]=4 mentre il nodo t ha un costo d[t]=9
Quindi seleziono il nodo 1 e lo aggiungo ai nodi già visitati S.
$$ L = \{ t \} \\ S=\{ s, 2, 1 \} $$
Poi analizzo gli archi in uscita dal nodo 1.
Ce n'è uno solo verso il nodo t.
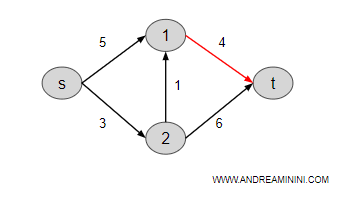
Il costo del cammino dal nodo 1 al nodo t è minore del costo d[t]
$$ d_1+c_{1t}= 4+4 = 8 < d_t = 9 $$
Quindi, posso aggiornare il costo del cammino e il predecessore del nodo t
$$ d = [ 0, 4, 3, 8 ] $$
$$ pred = [ s, 2, s, 1 ] $$
Non aggiungo il nodo t nella lista dei nodi da visitare perché è già presente
$$ L= \{ \} $$
Iterazione 4
Nell'interazione successiva estraggo il nodo t da L.
Il nodo t viene aggiunto nella lista S dei nodi già visitati.
$$ L = \{ \} \\ S=\{ s, 1, 2, t \} $$
Il nodo t non ha alcun nodo in uscita.
Iterazione 5
La lista dei nodi da visitare L è vuota.
$$ L = \{ \} $$
L'algoritmo termina qui.
Le etichette dei vettori d e pred diventano etichette permanenti:
$$ d = [ 0, 4, 3, 8 ] \\ pred = [ s, 2, s, 1 ] $$
Il risultato finale
Il cammino a costo minore dal nodo s al nodo t si individua dal vettore pred.
$$ pred = [ s, 2, s, 1 ] $$
ossia
$$ pred[s]=s \\ pred[1]=2 \\ pred[2]=s \\ pred[t]=1 $$
Parto dal nodo finale (t) e rilevo il nodo precedente.
E' il nodo 1.
$$ pred[t]=1 $$
Poi vedo qual è il miglior nodo precedente del nodo 1.
E' il nodo 2.
$$ pred[1]=2 $$
Infine, cerco qual è il miglior nodo precedente del nodo 2.
E' il nodo s
$$ pred[2]=s $$
Ho così trovato a ritroso il cammino a costo minore da s a t.
E il cammino s,2,1,t.
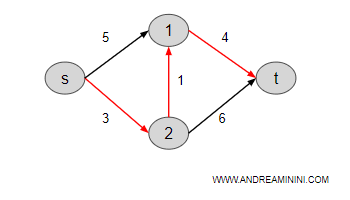
Nota. Il percorso s-2-1-t costa 8 ( ossia 3+1+4 ) e ha un costo del cammino minore rispetto agli altri cammini possibili che congiungono il nodo s e il nodo t sul digrafo. Ad esempio, i percorsi alternativi s-1-t e s-2-t costano entrambi 9. Quindi, costano di più.
L'algoritmo di Dijkstra in Python
Ecco l'implementazione dell'algoritmo di Dijkstra in Python
L'ho realizzato per risolvere l'esempio precedente
- import numpy as np
- d = np.array([0,None,None,None])
- pred = np.array([0,1,2,3])
- grafo = np.array([[0,5,3,0],[0,0,0,4],[0,1,0,6],[0,0,0,0]])
- L=set([0])
- S=set([])
- while (len(L)>0):
- # seleziona un nodo (x= da L con distanza minore dal nodo iniziale
- z=None
- x=None
- for i in L:
- if ((z==None) or (d[i]<z)):
- z=d[i]
- x=i
- L.remove(x)
- S.add(x)
- k=0
- for i in grafo[x]:
- if ((i > 0)&(k not in S)):
- node_ad=k
- L.add(node_ad)
- if ((d[k]==None) or (d[x]+grafo[x,k]<d[k])):
- d[k]=d[x]+grafo[x,k]
- pred[k]=x
- k=k+1
- print("nodo=",x,", L=",L,", S=",S,", d=", d,", pred=", pred)
In questo caso s=0 e t=3.
Le connessioni e i costi degli archi del digrafo sono rappresentati con una matrice di adiacenza.
I costi degli archi sono i valori nella matrice. Dove il valore 0 indica nessun arco tra i nodi.
L'output del programma è il seguente:
nodo= 0 , L= {1, 2} , S= {0} , d= [0 5 3 None] , pred= [0 0 0 3]
nodo= 2 , L= {1, 3} , S= {0, 2} , d= [0 4 3 9] , pred= [0 2 0 2]
nodo= 1 , L= {3} , S= {0, 1, 2} , d= [0 4 3 8] , pred= [0 2 0 1]
nodo= 3 , L= set() , S= {0, 1, 2, 3} , d= [0 4 3 8] , pred= [0 2 0 1]
In quattro iterazioni il programma ha trovato il percorso a cammino inferiore dal nodo s=0 al nodo t=3 del digrafo.
Analizzando a ritroso il vettore pred[] ricostruisco il percorso ottimale.
pred[4] = 1
pred[1]=2
pred[2]=0
Quindi, il percorso ottimale è 0⇒2⇒1⇒4
E così via.
