Come trovare il cammino ottimale in un digrafo
Il cammino ottimale in un digrafo è il cammino con costo più basso tra tutti i cammini possibili da un nodo di origine a un nodo di destinazione.
Esistono diversi algoritmi di ricerca per cercarlo, più o meno efficienti.
Esempio
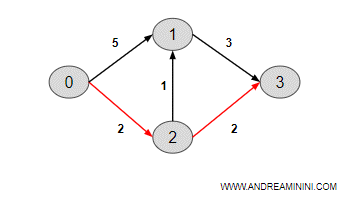
Devo trovare il cammino ottimale dal nodo 0 al nodo 3.
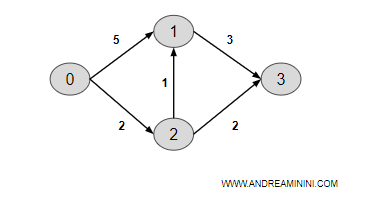
Il digrafo è composto da 4 nodi e 5 archi.
Creo un vettore NV con i nodi da visitare inserendo inizialmente soltanto il nodo di partenza (0) .
$$ NV = \{ 0 \} $$
Poi creo un vettore con i costi del percorso CP dal nodo 0 al nodo n-esimo
Inizialmente assegno a tutti un costo infinito e zero al primo elemento.
$$ CP = \{ 0 , ∞ , ∞ , ∞ \} $$
Infine creo un vettore PR dove indico i predecessori dei nodi.
Inizialmente assegno a ogni nodo se stesso come predecessore.
$$ PR = \{ 0 , 1 , 2 , 3 \} $$
Un algoritmo di ricerca è il seguente:
- Estraggo un nodo da visitare da NV.
- Analizzo gli archi in uscita e calcolo il costo del percorso al nodo adiacente.
- Se il costo al nodo adiacente è inferiore al costo indicato nel vettore CP, aggiorno il vettore CP e il vettore PR.
- Aggiungo i nodi adiacenti al vettore NV dei nodi da visitare.
- L'algoritmo termina quando non ci sono più nodi da visitare nel vettore NV
Ciclo 1
Estraggo ed elimino il nodo 0 dal vettore NV.
Gli archi in uscita dal nodo 0 sono collegati ai nodi adiacenti 1 e 2.
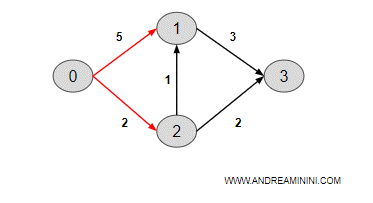
Calcolo il costo del cammino da 0 a 1 e da 0 a 2.
- c1 = 0+5= 5
- c2 = 0+2 =2
I costi sono inferiori a quelli del vettore CP.
$$ CP = \{ 0 , ∞ , ∞ , ∞ \} $$
Quindi, aggiorno il vettore CP con i nuovi dati.
$$ CP = \{ 0 , 5 , 2 , ∞ \} $$
Poi aggiorno i predecessori dei nodi 1 e 2 inserendo il nodo 0.
$$ PR = \{ 0 , 1 , 2 , 3 \} $$
$$ PR = \{ 0 , 0 , 0 , 3 \} $$
Infine, aggiungo i nodi 1 e 2 ai nodi da visitare.
$$ NV = \{ 1, 2 \} $$
Ciclo 2
Estraggo ed elimino il nodo 1 dal vettore NV.
Il nodo 1 ha un solo arco in uscita verso il nodo adiacente 3.
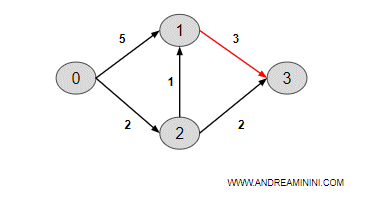
Calcolo il costo del cammino da 1 a 3.
- c3 = c1+3 = 5+3= 8
Il costo c3=8 è inferiore a quello del vettore CP ossia a ∞.
$$ CP = \{ 0 , 5 , 2 , ∞ \} $$
Quindi, aggiorno il costo c3 sul vettore CP
$$ CP = \{ 0 , 5 , 2 , 8 \} $$
Poi aggiorno il vettore dei nodi predecessori inserendo pred(3)=1.
$$ PR = \{ 0 , 0 , 0 , 1 \} $$
Infine, aggiungo il nodo 3 ai nodi da visitare.
$$ NV = \{ 2, 3 \} $$
Ciclo 3
Estraggo ed elimino il nodo 2 dal vettore NV.
Il nodo 2 ha due archi in uscita che lo connettono ai nodi adiacenti 1 e 3.
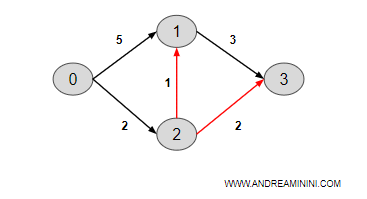
Calcolo il costo del cammino da 2 a 1 e da 2 a 3.
- c1 = c2+1= 2+1=3
- c3 = c2+2 =2+2=4
I costi c1=3 e c3=4 sono inferiori a quelli nel vettore CP ossia 5 e 8.
$$ CP = \{ 0 , 5 , 1 , 8 \} $$
Quindi, aggiorno i costi nel vettore CP.
$$ CP = \{ 0 , 3 , 1 , 4 \} $$
Poi aggiorno i predecessori dei nodi 1 e 3 inserendo il nodo 2.
$$ PR = \{ 0 , 2 , 0 , 2 \} $$
Infine, aggiungo i nodi 1 e 3 ai nodi da visitare.
Il nodo 3 c'è già, quindi non lo riaggiungo.
$$ NV = \{ 1, 3 \} $$
Ciclo 4
Estraggo ed elimino il nodo 1 dal vettore NV.
Il nodo 1 ha un solo arco in uscita verso il nodo adiacente 3.

Calcolo il costo dal nodo 1 al nodo 3 con i costi aggiornati.
- c3 = c1+3 = 3+3= 6
Tuttavia, ora il costo c3=6 è superiore a quello nel vettore CP ossia a 4.
$$ CP = \{ 0 , 3 , 1 , 4 \} $$
Quindi, non faccio nulla e passo ad analizzare un altro nodo.
Ciclo 5
Estraggo ed elimino il nodo 3 dal vettore NV.
Il nodo 3 non ha archi in uscita.

Quindi, non faccio nulla e passo ad analizzare il nodo successivo.
Ciclo 6
Il vettore NV è nullo. Non c'è più nessun nodi da analizzare.
L'esecuzione dell'algoritmo termina qui.
Il risultato finale
La configurazione finale dei vettori al termine dell'esecuzione è la seguente:
$$ PR = \{ 0 , 2 , 0 , 2 \} $$
$$ CP = \{ 0 , 3 , 1 , 4 \} $$
Il vettore PR mi dice quali sono i nodi predecessori ottimali per raggiungere un particolare nodo del digrafo.
$$ PR(0)=0 \\ PR(1) = 2 \\ PR(2)=0 \\ PR(3)=2 $$
Il vettore CP invece mi indica i relativi costi del percorso
$$ CP(0)=0 \\ CP(1) = 3 \\ CP(2)=1 \\ CP(3)=4 $$
Ora, analizzando a ritroso i nodi predecessori posso costruire il cammino ottimale.
Ad esempio per raggiungere il nodo 3 dal nodo 0.
$$ PR(3)=2 $$
$$ PR(2)=0 $$
Quindi, il cammino ottimale dal nodo 0 al nodo 3 è la seguenza di nodi
$$ 0 \rightarrow 2 \rightarrow 3 $$
Per un costo complessivo pari a 4.
$$ CP(3)=4 $$
L'algoritmo funziona ed è efficace.
Individua correttamente il cammino ottimale per spostarsi dal nodo 0 al nodo 3.
Tuttavia, non è l'algoritmo più efficiente possibile.
Nota. L'algoritmo ripassa sugli stessi nodi più volte. La complessità dipende dal numero dei nodi (n) , degli archi (m) e dal massimo valore assoluto dei costi negli archi (|cmax|). Per una complessità pari a $$ O( nm|c_{max}| ) $$ Quanto più alti sono i costi degli archi, tante più volte dovrà ripassare sugli stessi archi per ridurre il costo del percorso/cammino.
Ci sono molti altri algoritmi più performanti e varie implementazioni più efficienti.
Ad esempio, l'algoritmo di Dijkstra evita di ripassare sugli stessi nodi.
E così via.
