La funzione linalg lstsq di python

La funzione linalg.lstsq mi permette di trovare le soluzioni dei sistemi di equazioni non quadrati, quelli con un numero diverso di incognite e di incognite. E' una funzione di algebra lineare della libreria numpy.

linalg.lstsq(x,b)

Il primo argomento (x) è la matrice dei coefficienti del sistema di equazioni.

Il secondo argomento (b) è il vettore dei termine noti.

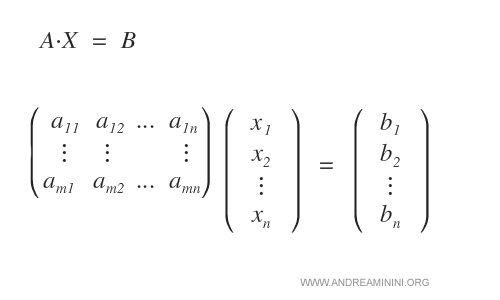
Nota. L'equazione può essere sovra o sottodeterminata. La funzione risolve l'equazione ax=b by elaborando un vettore che minimizza la norma euclidea ||b-ax||^2. Calcola i minimi quadrati di un sistema di equazioni a matrice lineare.

Un esempio pratico

Come prima cosa, importo in memoria il modulo numpy.

import numpy as np

Poi prendo un sistema di equazioni con due equazioni e tre incognite.

E' un sistema di equazione non quadrato che non potrebbe essere risolto con la funzione linalg.solve.

$$ \begin{cases} 2x+y=3 \\ x+5y+2z=1 \end{cases} $$

Definisco la matrice dei coefficienti e il vettore dei termini noti tramite la funzione array().

Li assegno rispettivamente alla variabile a e b.

a=np.array([[2,1,0],[1,5,2]])
b=np.array([3,1])

Per trovare le soluzioni del sistema di equazioni uso la funzione linalg.lstsq().

np.linalg.lstsq(a,b)

Il risultato della funzione è il seguente:

(array([ 1.48514851, 0.02970297, -0.31683168]), array([], dtype=float64), 2, array([5.64150235, 1.78141832]))

La funzione restituisce la lista con le soluzioni delle incognite del sistema.

$$ \begin{pmatrix} x=1.485 \\ y=0.029 \\ z=-0.316 \end{pmatrix} $$

E così via.