La funzione linalg solve di python

Per risolvere un sistema di equazioni con il linguaggio python, utilizzo al funzione matematica linalg.solve() della libreria numpy.

linalg.solve(x,b)

Dove il primo argomento x è la matrice dei coefficienti del sistema, mentre il secondo argomento b è il vettore dei termini noti.

E' uno strumento di python utile per cercare le soluzioni di un problema di algebra lineare.

Attenzione. La funzione linalg.solve risolve soltanto i sistemi lineari quadrati. Sono i sistemi in cui il numero delle incognite eguaglia il numero delle equazioni. Per risolvere sistemi non quadrati (not square matrix) si può usare la funzione linalg.lstsq().

Un esempio pratico

Apro python e carico in memoria il modulo numpy.

import numpy as np

Dato un sistema di equazioni generico a tre incognite:

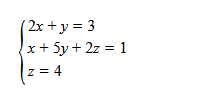
La matrice dei coefficienti e la matrice dei termini noti del sistema sono le seguenti:a

$$ A = \begin{pmatrix} 2 & 1 & 0 \\ 1 & 5 & 2 \\ 0 & 0 & 1 \end{pmatrix} $$

$$ B = \begin{pmatrix} 3\\ 1 \\ 4 \end{pmatrix} $$

Definisco la matrice e il vettore su python tramite la funzione array().

Le associo alle variabili A e B

A=np.array([[2,1,0],[1,5,2],[0,0,1]])
B=np.array([3,1,4])

Per trovare le soluzioni del sistema uso la funzione linalg.solve().

np.linalg.solve(A,B)

La funzione restituisce in output questo risultato

array([ 2.44444444, -1.88888889, 4.])

La lista contiene le soluzioni delle incognite del sistema.

$$ \begin{pmatrix} x=2.44 \\ y=-1.88 \\ z=4 \end{pmatrix} $$

E così via.