Indice di Shannon-Wiener
L'indice di Shannon-Wiener è un indice statistico per misurare la diversità di una popolazione. E' stato ideato dall'ingegnere Claude Shannon e dal matematico Norbert Wiener.
Indice di Shannon-Wiener o Shannon-Weaver? In molti testi l'indice è presentato erroneamente come indice di Shannon-Weaver, dal nome di Warren Weaver con cui Shannon lavorò a un noto modello della teoria dell'informazione ( modello Shannon-Weaver ).
A cosa serve?
E' utilizzato nel machine learning per individuare la caratteristica più utile su cui costruire un albero decisionale.
Come funziona l'indice di Shannon Wiener
Partiamo da una popolazione X ha una caratteristica con n modalità (m1,..,mn).
Ogni modalità ha una probabilità di verificarsi P(mi).
La formula dell'indice di Shannon-Wiener è la seguente:
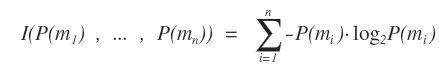
In genere è indicata con la lettera H o H'.
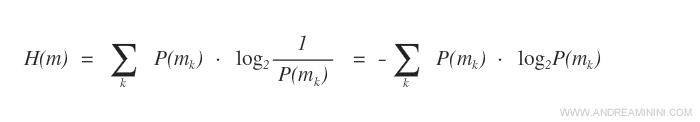
Come significa l'indica H di Shannon Wiener?
L'indice di Shannon-Wiener misura l'efficacia della risposta riguardo a Y fornita dall'attributo X.
- H tendende a zero ( attributo utile ). L'informazione è molto utile perché fornisce delle risposte nette. La diversità è minima.
- H tendente a 1 ( attributo inutile ). L'informazione è inutile perché fornisce delle risposte vaghe. La diversità è massima.
Nota. In alcuni testi di intelligenza artificiale invece di diversità si utilizza il termine entropia. Il significato è comunque sempre lo stesso. Il contributo di un attributo all'albero decisionale è misurabile dall'entropia (diversità) delle informazioni residuali dopo averlo selezionato ( cd valore informativo residuale ).
Quindi il valore informativo V dell'attributo m è uguale a:
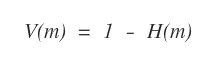
L'attributo con il valore informativo (V) più alto è l'attributo migliore per cominciare a costruire l'albero decisionale.
Un esempio pratico
La macchina deve costruire un albero decisionale a partire da una serie di esempi detti insieme di adestramento.
Per ogni esempio (riga) viene rilevato lo stato di dieci caratteristiche X e l'esito finale Y.
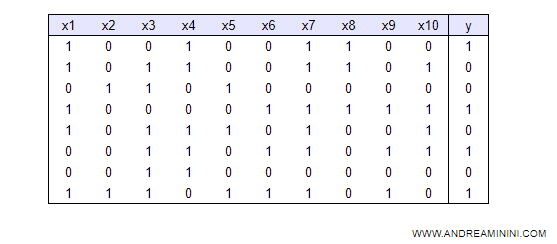
Nota. Per semplicità ogni caratteristica X è misurata con una variabile booleana e ha soltanto due modalità: 0 ( non rilevata ) e 1 ( rilevata ). Ad esempio, la caratteristica X1 potrebbe essere "trend del prezzo" con 1 associato a crescente ( uptrend ) e 0 a decrescente ( downtrend ). La caratteristica X2 a lunedì con 1 ( è lunedì ) e 0 ( non è lunedì ). E così via.
Comincio con l'analisi della prima caratteristica X1.
La caratteristica x1 viene rilevata 5 volte su 10 esempi.
Pertanto, ha una probabilità di esistenza p(x1) di 0.5.
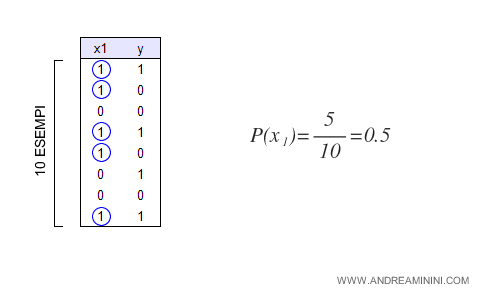
Nelle cinque volte in cui viene rilevata la caratteristica X1, l'evento Y si verifica 3 volte su 5.
Quindi, la probabilità che ci sia una relazione tra X1 e Y è pari a 3/5 ossia 0.6.
La probabilità che non ci sia è pari a 2/5 ossia 0.4.
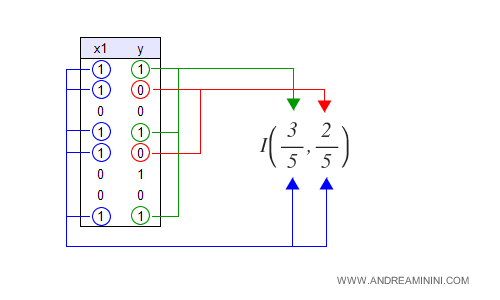
L'indice di Shannon-Wiener per la caratteristica X1 è 0.966.
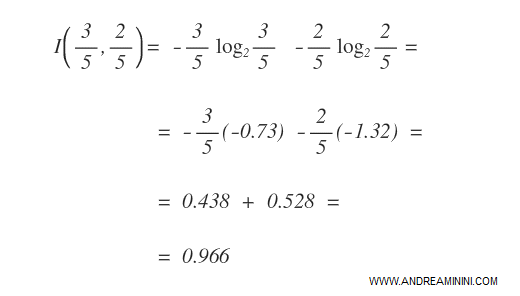
Ripeto il calcolo dell'indice H di Shannon-Wiener per tutte le Xn caratteristiche dell'insieme di addestramento.

Gli attributi X6 e X9 sono i più promettenti perché distinguono nettamente i casi positivi da quelli negativi.
Da queste caratteristiche si ottiene una classificazione migliore.
Quindi, un albero decisionale ( decision tree ) costruito a partire da questi due attributi è molto più efficiente e meno profondo rispetto agli altri.
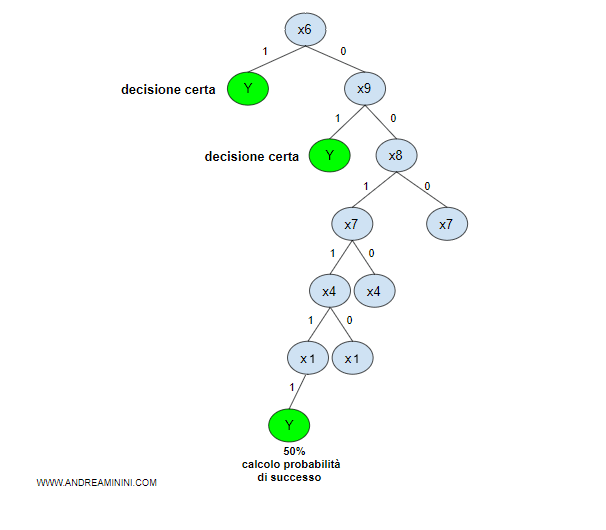
Nota. Il precedente esempio è tratto dagli appunti come costruire un albero decisionale efficiente a cui riamando per ogni ulteriore spiegazione.
Complessivamente, il valore informativo della selezione è 1-H.
In questo caso, dopo aver scelto x6 o x9 il valore V resta uguale a 1 ( valore massimo ).
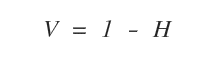
Tuttavia, il lavoro non è ancora finito.
In un algoritmo di scelta completo occorre considerare anche il valore informativo delle scelte successive ( valore informatio residuale ).
Il valore informativo residuale
Nel precedente esempio ho calcolato soltanto il primo livello scelta.
Ora devo calcolare anche il valore informativo residuo R scendendo più in profondità.
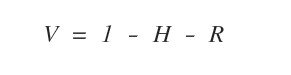
Soltanto in questo modo posso sapere se conviene scegliere l'attributo oppure no.
Esempio
Una volta verificate le caratteristiche X6 e X9 , se entrambe sono false quali altri attributi occorre valutare?
L'insieme di addestramento si riduce ai soli casi in cui x6 o x9 sono false.
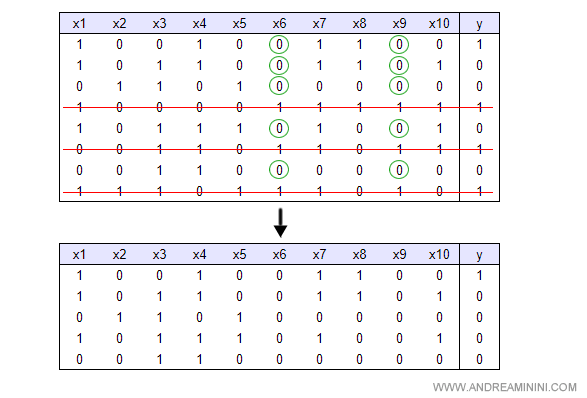
Tra i casi residui soltanto una riga è associata a un evento positivo di Y ( la prima riga ).
Questo mi permette di valutare il valore informativo delle variabili di secondo livello.
In questo caso, l'indice H va moltiplicato per la probabilità p(x) della variabile.
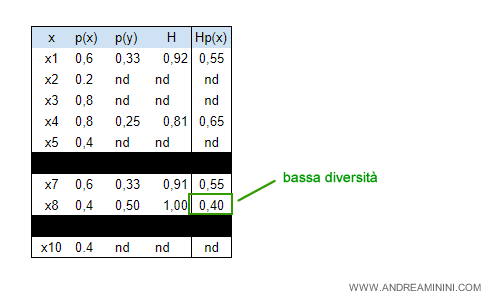
Esempio. La variabile x1 si presenta 3 volte su 5, quindi la sua probabilità p(x) è pari a 3/5 ossia 0,6. Nelle tre volte in cui si presenta, soltanto in un caso y=1. Pertanto, la probabilità p(y) è pari a 033. Questi dati mi permettono di calcolare l'indice H per x1 con la formula di Shannon Wieser. Poi moltiplico H per p(x) ottenendo il valore 0,55. La stessa procedura devo ripeterla per le altre variabili x2, x3, ...
Quale variabile di 2° livello è meglio scegliere?
La variabile x8 fornisce il valore Hp(x) più basso (0,4).
Posso selezionarla come variabile di secondo livello dell'albero decisionale.
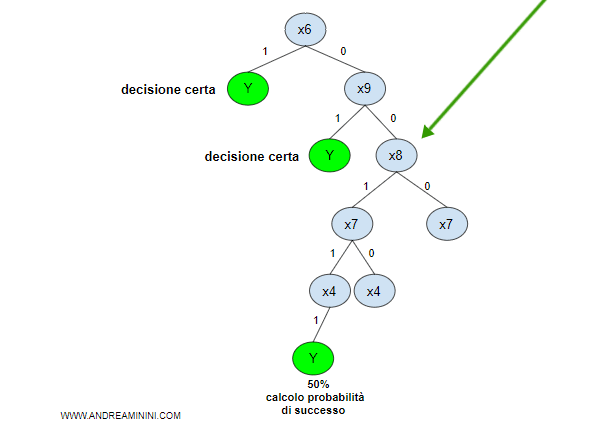
Adesso il valore informativo aggiornato dell'albero decisionale è il seguente:
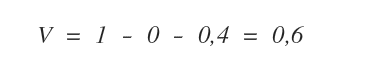
A questo punto posso ripetere la procedura per selezionare le variabili di terzo livello.
E così via fino a raggiungere i nodi terminali.
Problemi e criticità dell'indice di Shannon Wiener
L'indice di Shannon Wiener tende a favorire gli attributi con molti valori.
E' quindi consigliabile normalizzare il guadagno dell'informazione V per la quantità di informazione necessaria a determinare il valore.
