Come costruire un albero decisionale
Una macchina apprende dall'esperienza se riesce a costruire da sé un albero decisionale in base ai dati osservati.
A cosa servono gli alberi decisionali? Consentono alla macchina di prendere una decisione operativa in base alla situazione ambientale in cui si trova. Tuttavia, non devono essere scritti dal progettista. E' la macchina a doverli realizzare automaticamente.
In questi appunti spiego come costruirne uno tramite le tecniche di apprendimento induttivo supervisionato.
Un esempio pratico
L'agente deve prendere una decisione Y.
Nota. La decisione può essere di qualsiasi tipo. Ad esempio, accendere le luci o spegnerle. Inoltre, per semplicità in questo esempio considero soltanto variabili booleane che possono avere valore vero (si) o falso (no).
Il supervisore fornisce alla macchina un elenco di esempi in cui Y è associato a un vettore di fattori X.
E' detto insieme di addestramento ( o training set ).
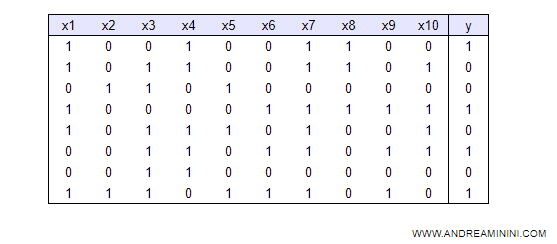
I vari fattori X1, X2, ... , Xn sono informazioni derivanti dall'osservazione dell'ambiente esterno.
Ad esempio, X1 potrebbe essere l'attributo "è mattina?", X2 l'attributo "sta piovendo?", "è domenica?", ecc.
In questo caso gli attributi sono variabili booleane e possono avere valore vero (1) o falso (0).
Nota. Gli attributi possono anche avere modalità qualitative per classi ( es. buono, discreto, ecc. ) o quantitative con valori numerici non booleani ( es. 1123, 27, ecc. ). Tuttavia, analizzare questi aspetti complicherebbe inutilmente questa spiegazione, perché ogni valore andrebbe considerato come attributo a se stante. Per questa ragione utilizzo soltanto i valori booleani. Sono più semplici da capire.
E l'albero decisionale?
Al momento non c'è ancora un albero decisionale perché la macchina deve costruirlo.
In questo caso il progettista non ha fornito un decision tree all'agente ma soltanto dei dati.
La macchina deve analizzare gli esempi per trovare le relazioni di causalità tra Y e gli elementi del vettore X.
In pratica, deve costruire una funzione di verità.
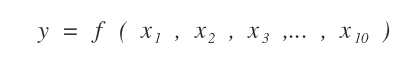
C'è però un problema, ogni funzione di verità è un albero decisionale a se tante.
Quindi non esiste un solo albero decisionale.
Esempio. L'agente potrebbe cominciare a confrontare X1, poi X2, X3, ecc. per costruire un albero decisionale. Tuttavia, potrebbe costruirne un altro se iniziasse a confrontare prima X2, poi X3, X1, ecc. usando una sequenza diversa nei test. E così via.
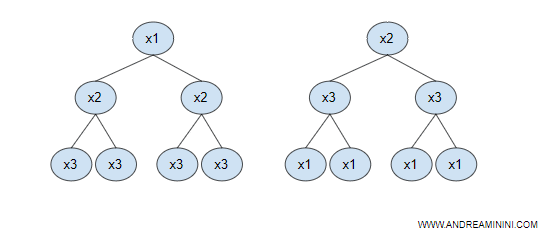
In questo caso il vettore è composto da dieci fattori { X1, X2, ... , X10 }.
Quindi ci sono 10! permutazioni ossia 3.628.800 alberi decisionali tra cui scegliere.
Emergono così due problemi:
- Qual è l'albero decisionale migliore?
- Come trovarlo?
Nota. La ricerca completa è da evitare perché avrebbe una complessità eccessiva. Considerando che ogni albero decisionale ha 210=1024 ramificazioni / test da analizzare, trovare il decision tree più efficace ed efficiente è un problema serio. La complessità della ricerca aumenta in modo esponenziale con l'aggiunta di nuove variabili. Ad esempio, se aggiungessi una sola variabile booleana (x11) al vettore, ogni albero avrebbe ben 211=2048 ramificazioni e così via.
Come trovare l'albero decisionale migliore
Un'euristica efficace consiste nell'individuare i fattori più importanti, quelli che influiscono di più sul risultato finale (Y).
Nell'albero decisionale i fattori più importanti devono essere analizzati prima degli altri.
In questo modo, l'agente può scartare subito le ramificazioni inutili.
Per trovare i fattori determinanti l'agente confronta ogni singolo fattore X con il risultato y.
Come trovare l'attributo migliore in modo automatico? Per trovare algoritmicamente i nodi più promettenti potrei anche utilizzare il coefficiente di Gini o l'indice di Shannon-Wieser.
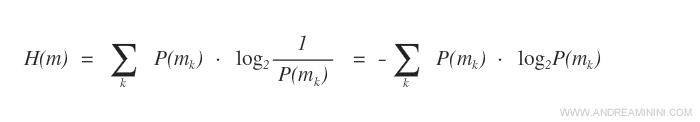
Tuttavia, in questa pagina non userò l'indice Shannon Wiener. Preferisco effettuare la selezione manuale per spiegare meglio la logica del funzionamento della selezione.
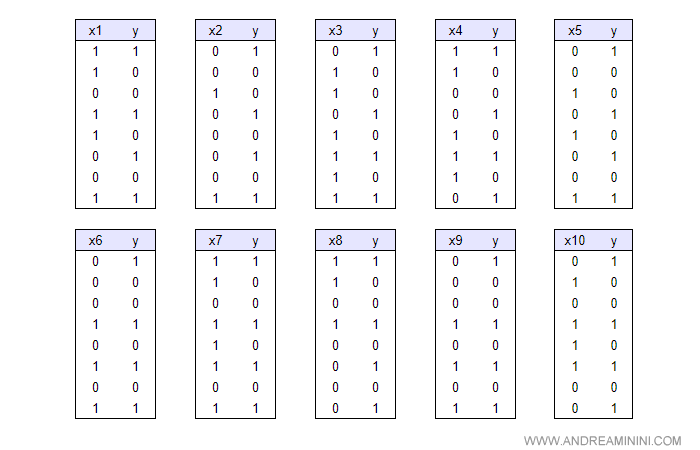
Per leggere meglio le tabelle, le riscrivo con il fattore X in ordine crescente.
In questo modo è più facile individuare degli schemi ( pattern ) anche a occhio nudo.
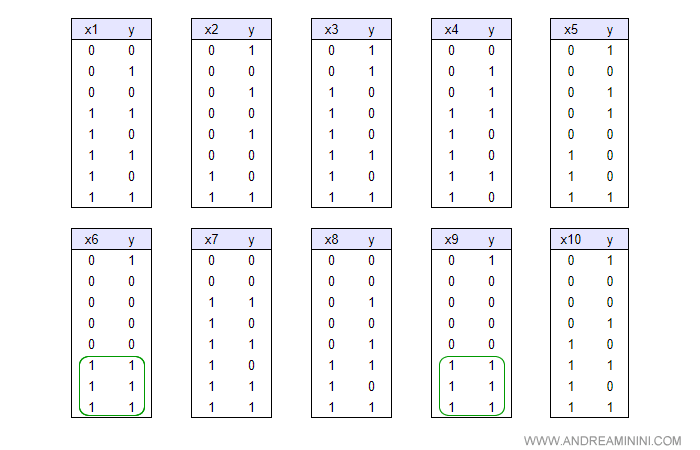
Nelle variabili X6 e X9 l'agente rileva uno schema utile.
Negli esempi analizzati, quando X6 è vera, la variabile Y è sempre vera. Lo stesso accade con la variabile X9.
Nota. Non è detto che ci sia una reale relazione di causa-effetto tra X6 e Y perché l'agente sta osservando soltanto l'insieme degli esempi, ossia un campione di dati della realtà. E' uno dei problemi tipici del ragionamento per induzione.
Quindi, l'agente può scegliere indifferentemente il fattore X6 o X9 come primo nodo dell'albero decisionale e l'altro come secondo nodo.
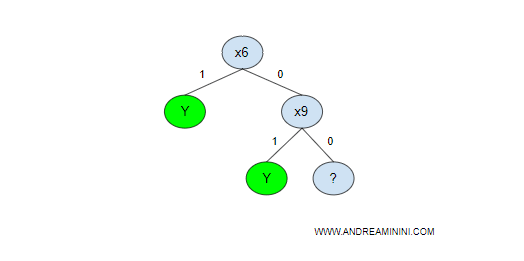
Esempio. Se al primo test l'agente rileva X6 vera, può prendere immediatamente la decisione ( Y=1 ) senza fare altri confronti. Se X6 è falsa, passa a confrontare il secondo nodo X9. Se X9 è vera, prende la decisione ( Y=1 ). Quindi, se X6 è vera basta un solo ciclo per trovare la risposta. Se X9 è vera bastano al massimo due cicli. In entrambi i casi la ricerca viene interrotta dopo aver trovato la risposta. I nodi Y sono nodi-foglie terminali dell'albero.
L'albero decisionale non è ancora finito.
Come si può facilmente notare, se entrambe le variabili X6 e X9 sono false l'agente non riesce a prendere una decisionale.
L'agente deve costruire altre ramificazioni nei nodi aperti e non terminali ( quello con il simbolo ? ).
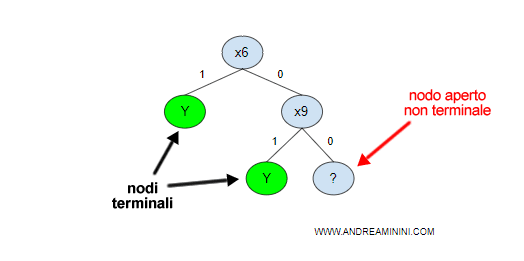
A questo punto l'agente cerca nelle tabelle altri fattori determinanti di secondaria importanza nei dati restanti.
Per farlo seleziona soltanto i dati condizionati al valore falso di X6 e di X9.
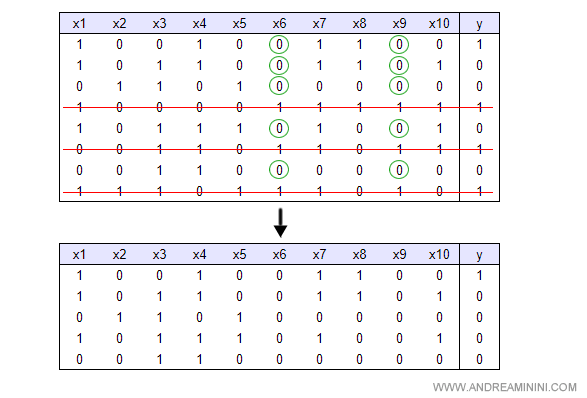
Nota. La macchina non prende più in considerazione le variabili X6 e X9 perché le ha già incluse nell'albero decisionale. Inoltre, la ricerca è limitata alle ramificazioni sotto il nodo ancora incerto dell'albero decisionale, quello con i valori falsi di entrambe le variabili X6 e X9. Gli altri casi ( es. X6 falso e X9 vero, ecc. ) l'agente non deve più analizzarli perché ha già ottenuto una risposta utile.
Poi mette in relazione i fattori residui { X1,X2,X3,X4,X5,X7,X8,X10 } con la variabile decisionale Y.
Anche in questo caso per semplicità ordino le tabelle per X crescente.
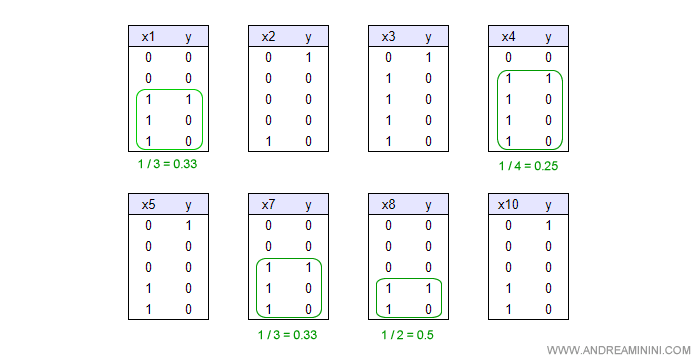
Dall'analisi emergono altre tre variabili ( X1, X4, X7, X8 ) con una relazione a Y.
Nota. Le altre variabili ( X2, X3, X5, X10 ) possono essere subito scartate perché non hanno alcuna relazione con Y. Sono diventate ininfluenti.
Nelle variabili ( X1, X4, X7, X8 ) non si riscontra un pattern certo, perché in nessun caso il valore positivo delle variabili restituisce al 100% il valore Y=1.
Quindi, l'agente non può scegliere il nodo successivo.
Può comunque continuare la costruzione dell'albero in termini probabilistici.
La variabile X8 ha il 50% di probabilità di successo. E' più alta rispetto a X7 (33%), X1 (33%) e X4 (25%).
Quindi X8 viene scelta come nodo successivo.
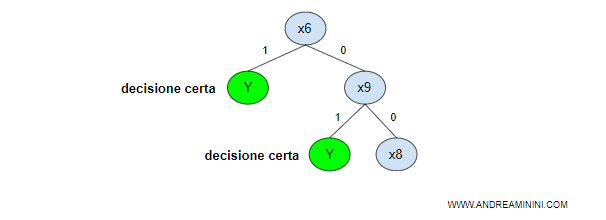
A questo punto l'agente può restringere ulteriormente la base dati.
I dati restanti a partire dal nodo x8 sono soltanto i seguenti:
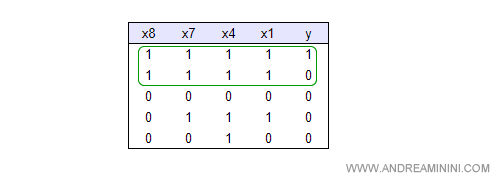
L'unica possibilità di successo si ottiene quando anche X7 , X1 e X4 sono veri.
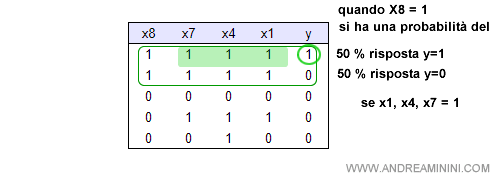
Quando x8 = x1 = x4 = x7 = 1 c'è una risposta positiva y=1 e una risposta negativa y=1.
Quindi, la probabilità di risposta positiva è del 50%.
Escludendo le probabilità di successo inferiori al 50%, l'albero decisionale è il seguente:
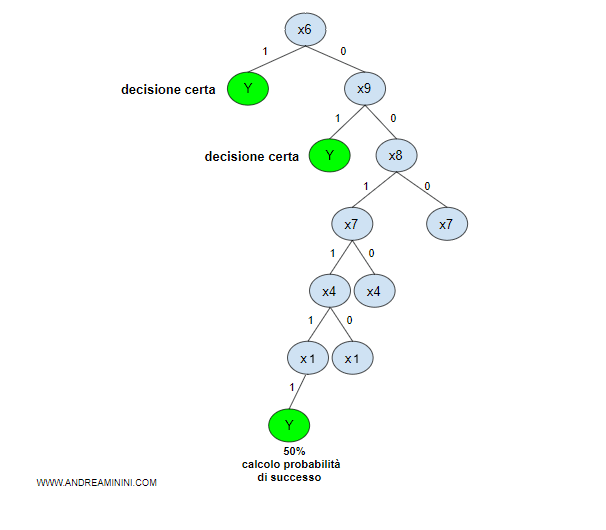
Il processo di apprendimento induttivo della macchina finisce qui.
L'agente ha costruito automaticamente l'albero decisionale più efficiente possibile per la decisione Y.
Nota. Nel peggiore dei casi l'agente raggiunge una risposta utile dopo sole 5 iterazioni ( test ). E' l'albero decisionale più efficiente tra tutti.
La valutazione della qualità dell'albero decisionale
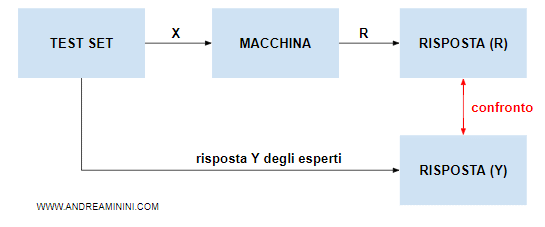
Una volta costruito, le risposte dell'albero decisionale sono confrontate con quelle di un insieme di test ( o testing dataset ) realizzato da esperti in materia.
L'albero supera la valutazione di qualità se fornisce le stesse risposte dell'insieme di test.
Il salvataggio e l'aggiornamento dell'albero decisionale
Alla fine del processo di machine learning l'agente salva l'albero decisionale in memoria.
Così facendo può richiamarlo ogni volta che deve prendere la decisione Y senza doverlo ricalcolare.
Quando conviene fare l'aggiornamento dell'albero decisionale? Nel corso del tempo la macchina alimenta il database degli esempi con altri casi osservati direttamente dall'ambiente ( feedback ) o immessi dal supervisore. Quindi, periodicamente l'agente deve ricalcolare l'albero decisionale sulla base dei nuovi dati aggiornati e dell'esperienza.
I problemi nella costruzione dell'albero decisionale
Nel corso della costruzione dell'albero di decisione potrebbero verificarsi dei problemi operativi. I più frequenti sono i seguenti:
- Dati mancanti su un attributo. In alcuni esempi un attributo potrebbe non essere documentato. In questi casi, il ramo si interromperebbe perché mancherebbero i nodi relativi all'attributo. Quindi, i dati di livello inferiore non potrebbero essere elaborati.
- Attributi con molti valori. Gli attributi con molti valori possono distorcere la selezione degli attributi rilevanti e aumentare il livello di complessità del decision tree.
- Attributi con valori continui. Un altro problema frequente è la presenza di attributi con valori continui, interi o discreti. Ad esempio, il prezzo, l'altezza, ecc.
