Metriche dei regressori

Le metriche più usate per analizzare l'errore (error analysis regression) di un algoritmo regressore nel machine learning supervisionato si basano sui residui ossia sulle differenze tra le previsioni del modello e le risposte corrette (target):

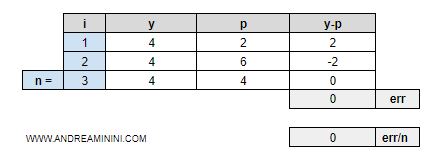
• Mean Error (ME). E' la media delle differenze tra previsioni (p) e target (y). Se la previsione è uguale al target, la differenza (p-y) è uguale a zero. Quindi, il tasso di errore del regressore è tanto più basso, quando più l'indicatore ME tende a zero. $$ ME = \frac{1}{n} \cdot \sum_{i=1}^n (y_i-p_i) $$

  Nota. Il semplice confronto tra il valore previsto (predizione) e il valore corretto (target) è una misura troppo semplificata che può indurre in errore perché le differenze con segno opposto si annullano tra loro. Ad esempio, se (y₁-p₁)=2 e (y₂-p₂)=-2 il tasso di errore ME è zero anche se le previsioni del modello non sono corrette.
  

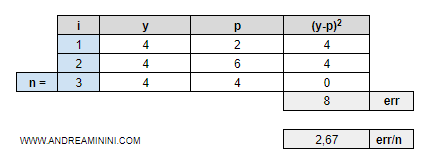
• Mean Squared Error (MSE). E' la media delle differenze al quadrato tra previsioni (p) e target (y). L'errore del regressore è nullo quando l'indicatore MSE=0. E' tanto maggiore quanto più l'indicatore MSE è maggiore di zero. $$ MSE = \frac{1}{n} \cdot \sum_{i=1}^n (y_i-p_i)^2 $$
  

  Nota. Nell'indicatore MSE le differenze di segno opposto non si compensano più. Questo indicatore rappresenta meglio il tasso di errore del regressore rispetto al precedente.
  

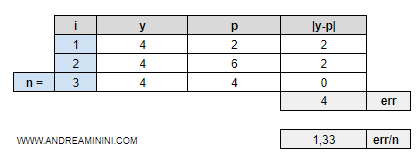
• Mean Absolute Error (MAE). E' la media delle differenze assolute tra previsioni e target. $$ MAE = \frac{1}{n} \cdot \sum_{i=1}^n |y_i-p_i| $$

  Nota. L'indicatore MAE è simile al MSE. Quanto più l'indicatore MAE tende a zero, tanto più il tasso di errori del regressore è basso. E viceversa.
  

• R² score. E' il coefficiente di determinazione, una proporzione tra variabilità e correttezza dei dati del modello. L'indicatore varia da -infinito (pessimo) a 1 (ottimo). Spesso è usato per confrontare un modello con un altro. Se R²=0 i due modelli sono simili.