Deterministic Finite Automaton

What is a deterministic finite automaton?

A deterministic finite automaton (DFA) is formally defined as a five-tuple: $$ A = (X, E, \delta, x_0, X_f) $$

It consists of the following components:

• X - a finite set of states
• E - a finite set of input symbols, called the alphabet
• δ - the state transition function
• x₀ - the initial state
• X_m - the set of accepting (or final) states

This structure is commonly known as a deterministic finite automaton (DFA).

Note. The term “finite-state” refers to the fact that the number of states X is finite. The automaton is “deterministic” because for each specific pair of a state and an input symbol, the transition function produces exactly one next state.

Representing a DFA

A deterministic finite automaton can be represented by either a transition table or a state transition diagram (graph).

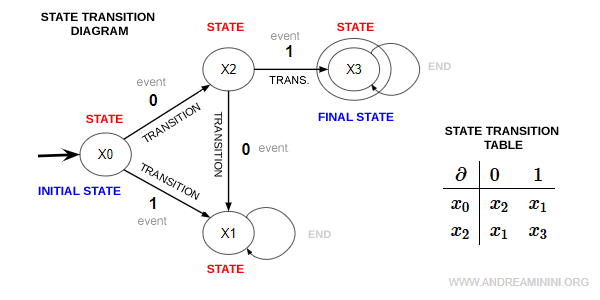
Note. In a transition table, rows correspond to states and columns correspond to input symbols.

In the diagram, each node represents a state, and each edge represents a transition between states.

$$ x_n = \delta(x_{n-1}, e_n) $$

The transition function takes as input a state (x_n-1) and a symbol (e) from the alphabet, where e represents an event.

The output is the next state (x_n).

The outgoing edges from a node x indicate which input symbols are valid transitions from that state.

In a DFA, every state must have exactly one defined transition for each symbol in the alphabet.

Note. A DFA has a finite and fixed amount of memory: once its set of states is defined, no additional states can be introduced.

However, not every pair (x_j, e_k) must have a corresponding transition. Some transitions may be undefined.

Events for which transitions are defined from a given state are called enabled events or active events, and they form the set A(x):

$$ A(x) = \{ e \in E \mid \partial(x, e)! \} $$

Here, the notation ∂(x,e)! means that the transition is defined.

From any given node, there cannot be two or more outgoing edges labeled with the same symbol.

A DFA always has exactly one initial state but may have several final states.

The initial state (x₀) is typically shown with an incoming arrow, while each final state (x₃) is represented by a double circle.

Note. A loop is an edge that connects a node to itself. It represents a situation where the automaton remains in the same state - that state becomes stable and does not change.

An Example

Consider an alphabet consisting of the symbols 0 and 1:

$$ E = \{ 0, 1 \} $$

The language consists of all words that begin with the substring 01:

$$ L = \{ w \in \{ 0, 1 \} \mid w \text{ begins with } 01 \} $$

The automaton reads an input string and checks whether the first character is 0 or 1.

If the first character is 0, it then checks whether the second character is 1.

The automaton can exist in four possible states:

$$ x_0 = \{ \} \\ x_1 = \{ 1 \lor 0,1 \} \\ x_2 = \{ 0 \} \\ x_3 = \{ 0, 1 \} $$

Note. In state x₁, the first character detected is 1. Since checking the second character would be redundant, the automaton proceeds directly to the next input string.

The initial state is x₀.

The corresponding state diagram is shown below:

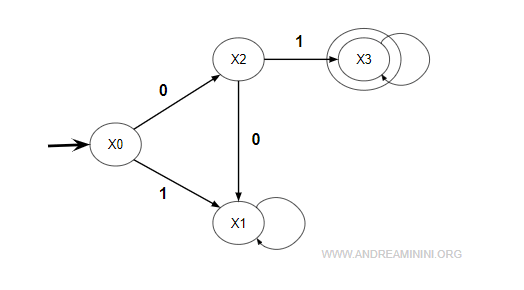
The corresponding transition table is:

$$ \begin{array}{c|lcr} \partial & 0 & 1 \\ \hline x_0 & x_2 & x_1 \\ x_1 & & \\ x_2 & x_1 & x_3 \\ x_3 & & \end{array} $$

Productions

A production is a sequence of transitions.

Each transition represents a change from one state to another caused by an event (e):

$$ x_n = \delta(x_{n-1}, e_n) $$

Thus, a production can be represented by a word formed from a sequence of input symbols (possibly repeated):

$$ e_1 e_2 e_3 \ldots e_k $$

Example. In the previous example, the transition from state X₀ to state X₃ corresponds to the production 01.

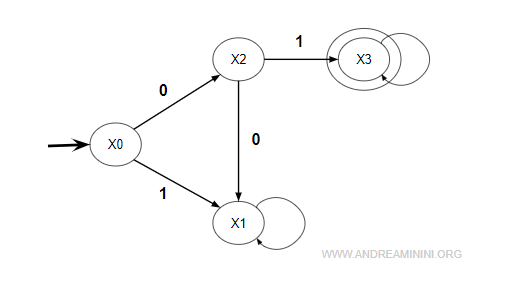
In the diagram, each production corresponds to a directed path from one node (state A) to another (state B).

States A and B do not necessarily need to be the initial or final states of the automaton.

Transitive and Reflexive Closure

The function δ* denotes the transitive and reflexive closure of δ. Starting from a state x, it reaches a state x_k through a specific production w: $$ \delta(x, w)! $$

To indicate that such a production exists, we write: $$ x_k = \delta^*(x, w)! $$

Example.

In the previous automaton, the path from node 0 to node 3 is written as:

$$ x_3 = \delta(x_0, 01) $$

Hence, the production w = 01 exists:

$$ \delta(x_0, 01)! $$

Note. The empty word ε allows any state x to remain unchanged. $$ x = \delta^*(x, w)! $$

Generated Words

A word w is generated by the automaton G = (X, E, δ, x₀, X_m) if there exists a production δ*(x₀, w)! that produces w starting from the initial state.

Accepted Words

A word w is accepted (or recognized) by the automaton G = (X, E, δ, x₀, X_m) if there exists a production δ*(x₀, w)! that starts from the initial state and ends in one of the accepting states.

In the diagram, an accepted word corresponds to a directed path from the initial node to a final node.

The set of all productions of a DFA defines the language recognized by the automaton.

Language of a Finite Automaton

In simple terms, the language of a deterministic finite automaton (DFA) is the collection of all event sequences w (called productions) that take the automaton from its initial state to any reachable state X_k.

So, the language represents all possible strings that can be formed using the automaton’s alphabet.

$$ L \subseteq E^* $$

Every DFA defines two closely related kinds of languages:

• The generated language
  This includes all strings that the automaton can possibly generate. $$ L(G) = \{ w \in E^* \mid \delta^*(x_0, w)! \} \subseteq E^* $$ In other words, it describes everything the system can do - all its potential behaviors.
• The accepted (or marked) language
  This is a smaller set: the strings that the automaton not only generates, but also accepts as valid. $$ L_m(G) = \{ w \in E^* \mid \delta^*(x_0, w) \in X_m \} \subseteq L(G) $$ These are the event sequences that bring the automaton to a specific goal or end condition.

  Example. Imagine a machine that turns off after a specific sequence of operations. The accepted language contains all those sequences that actually lead to the shutdown state.

Since every accepted word must first be generated, the accepted language is always a subset of the generated one:

$$ L_m(G) \subseteq L(G) $$

Note. The generated language is always prefix-closed: if a word is part of it, all its prefixes are also included. The accepted language, however, doesn’t necessarily follow this rule - it can stop only once a goal is reached.

The Class of DFA Languages

The set of all languages that can be accepted by deterministic finite automata is known as the class of DFA languages: $$ \mathcal{L}_{DFA} = \{ L \mid \exists \, G : L = L_m(G) \} $$

The class of generated languages is fully contained within this broader class of accepted languages.

For this reason, when we study automata, we usually focus on accepted languages - the ones that represent meaningful or complete behaviors of a system.

Proof idea. If a language is generated by some DFA G, we can easily build another DFA G′ that accepts it - just mark all states of G as final. However, the reverse isn’t true: some DFAs accept languages that no DFA can generate, because not all their states are accepting. Generated languages are always prefix-closed; accepted ones aren’t necessarily. That’s why the inclusion is strict.

And that’s the foundation for how automata define and classify formal languages.