Algoritmo di Levenshtein
L'algoritmo di Levenshtein misura la somiglianza tra due stringhe diverse. E' anche conosciuto come distanza di Levenshtein.
Quest'algoritmo è stato ideato nel 1965 dal russo Vladimir Levenshtein da cui prende il nome.
Quest'algoritmo è usato nel controllo ortografico dei wordprocessor per misurare la similarità tra due parole.
Come funziona l'algoritmo
Date due stringhe A e B, l'algoritmo misura il numero delle modifiche elementari necessarie per trasformare la stringa A nella stringa B.
Le operazioni elementari consentite sono le seguenti:
- eliminazione di un carattere
- sostituzione di un carattere con un altro
- inserimento di un nuovo carattere
Per spiegare il funzionamento dell'algoritmo è molto utile fare un esempio pratico.
Un esempio pratico
Per trasformare la parola "prova" in "provino" occorre
- sostituisco la lettera "a" con i alla quinta posizione della parola
prova -> provi
- inserisco la lettera "n" alla sesta posizione
provi -> provin
- inserisco la lettera "o" alla settima posizione
provin -> provino
Complessivamente, sono necessarie tre operazioni elementari.
Pertanto, in questo esempio la distanza di Levenshtein è uguale a 3.
Lo pseudocodice di Levenshtein
Ecco un esempio di pseudocodice dell'algoritmo
Date due stringhe str1 e str2 rispettivamente con n e m caratteri
str1="test"
str2="text"
Creo una matrice con n+1 righe e m+1 colonne
Poi numero la prima riga e la prima colonna da zero in poi.
for i to n+1
d[i][0]=i
for j to m+1
d[0][j]=j
Una volta inizializzata la matrice assume questa dimensione.
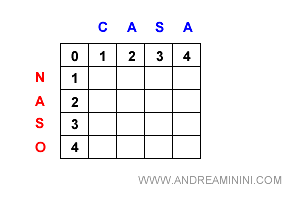
A questo punto leggo i caratteri delle due stringhe a partire dal primo carattere in poi.
- for i to n+1
- for j to m+1
- if (str1[i-1]==str2[j-1]):
- subcost=0
- else:
- subcost=1
- k=minimo{
- d[i-1][j]+1 // inserimento
- d[i][j-1]+1 // cancellazione
- d[i-1][j-1]+subcost //sostituzione
- }
- d[i][j]=k
Se i caratteri sono diversi l'algoritmo sceglie il minimo costo tra le operazioni di inserimento, cancellazione e sostituzione.
Ad esempio, il primo carattere C è diverso da N.
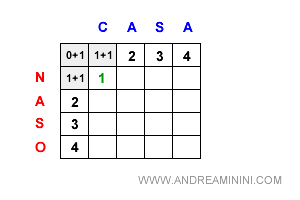
L'algoritmo addiziona 1 alle celle vicine precedenti (0+1, 1+1, 1+1) e seleziona quella con il costo minore.
In questo caso 0+1 = 1.
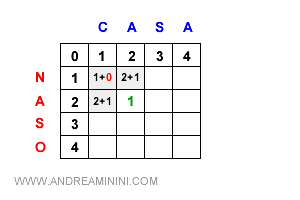
Nota. Nel caso in cui i caratteri sono uguali la costante subcost è uguale a zero (riga 4). Pertanto, uno dei valori non viene aumentato di uno (riga 10) ed è selezionato come valore minimo ( riga 7 ). In questo caso particolare, se i caratteri sono uguali la distanza di Levenshtein portata in avanti resta costante. Ad esempio, quando l'algoritmo confronta la lettera "a" di casa con la lettera "a" di naso, non incrementa uno dei valori (1+0). Quindi la cella mantiene lo stesso valore minimo della cella precedente ossia 1. E così via.
L'operazione viene iterata in avanti per tutte le celle restanti.
Al termine dell'elaborazione la distanza di Levenshtein è indicata sull'ultimo elemento in basso a destra della matrice.
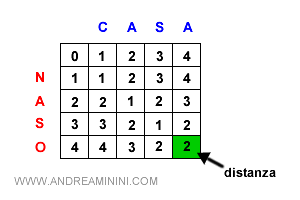
Per trasformare la stringa "casa" in "naso" sono necessarie 2 modifiche.
Ora la spiegazione del funzionamento dell'algoritmo di Levenshtein dovrebbe essere abbastanza chiara e comprensibile per tutti.
