La programmazione intera
Cos'è la programmazione intera
La programmazione intera è un modello usato nella ricerca operativa per risolvere problemi in cui le variabili di decisione possono assumere solo valori interi e/o binari (0/1).
Un modello di programmazione intera è caratterizzato da
- funzione obiettivo
- vincoli lineari
Le variabili del modello assumono valori interi (discreti) ossia non continui.
Esempio. Un problema tipico della programmazione intera riguarda una decisione che consiste nel compiere una determinata azione oppure no, scegliere tra un numero finito di alternative, ecc.
Un problema di programmazione interna è più difficile da risolvere rispetto a un problema di programmazione lineare perché le soluzioni vanno cercate esclusivamente tra i numeri interi anziché tra i numeri reali.
Come risolvere un problema di programmazione intera
Alcuni problemi di programmazione intera posso risolverli usando le tecniche di programmazione lineare (PL).
Esempio. Rimuovo il vincolo di interezza per risolvere il problema di ottimizzazione con l'algoritmo del simplesso della programmazione lineare. Poi arrotondo le soluzioni ottime da numeri reali a interi. La soluzione intera finale è approssimata ma talvolta soddisfacente. Questa tecnica di risoluzione è detta "rilassamento lineare".
Altri problemi, invece, sono risolvibili soltanto con la programmazione non lineare (PNL).
Questi ultimi sono i problemi più complessi perché appartengono alla classe dei problemi NP (non polinomiali).
Il modello di programmazione intera
Un modello di programmazione intera si presenta in questa forma a
$$ \min z(x) = \vec{c}^T \cdot \vec{x} \\ \begin{cases} A \cdot \vec{x} = \vec{b} \\ \\ \vec{x} \ge 0 \\ \\ \vec{x} \in Z^n \end{cases} $$
Dove z(x) è la funzione obiettivo da minimizzare.
I vettori c, x e b sono rispettivamente il vettore dei costi, delle variabili decisionali e dei termini noti mentre A è la matrice dei coefficienti del sistema.
Nota. Fin qui il modello è molto simile a quello della programmazione lineare. La differenza tra la programmazione lineare e la programmazione intera è la presenza del vincolo di interezza.
Il vincolo di interezza del modello è la condizione x ∈ Zn.
$$ \vec{x} \in Z^n $$
Vuol dire che le n variabili decisionali possono assumere solo valori compresi nell'insieme dei numeri interi Z.
Il problema di programmazione intera è detto
- ammissibile
se esiste un vettore x* di numeri interi che minimizza la funzione obiettivo z(x) $$ z^* \in Z^n $$ Il vettore x* è la soluzione del modello mentre z* è il valore ottimale della funzione obiettivo. - inammissibile
se non esiste un vettore x di numeri interi che minimizza la funzione obiettivo z(x). $$ z^*= + \infty $$ Il problema non ha soluzioni. In questi casi si dice che il problema è illimitato superiormente e si indica con il simbolo +∞.Nota. Allo stesso modo, se la funzione obiettivo è una funzione di massimizzazione max z(x) e non esiste un vettore x di numeri interi che massimizza la funzione obiettivo z(x) il problema è inammissibile. Non esistono soluzioni. In questo caso il problema è detto illimitato inferiormente e si indica con il simbolo -∞ $$ z^*= - \infty $$
Un esempio pratico
Questo problema include il vincolo di interezza
$$ min \ z(x)= 2x_1-x_2 \\ \begin{cases} x_1 + 2x_2 \ge 2 \\ 2x_1+x_2 \le 6 \\ -x_1+2x_2 \le 4 \\ x_1 - x_2 \le 2 \\ \\ x_1, x_2 \in Z \end{cases} $$
Rappresento graficamente i vincoli.
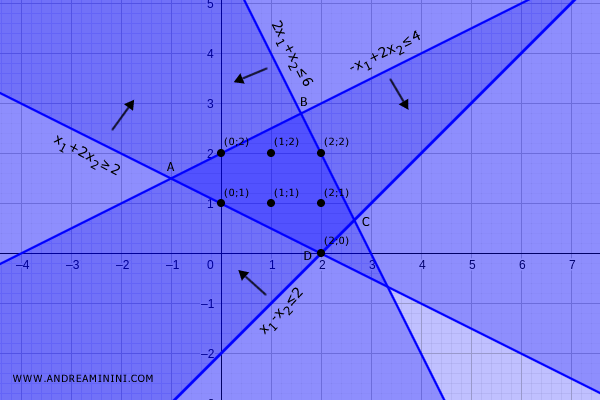
Nella programmazione intera l'insieme delle soluzioni ammissibili è composto dalle coppie (x1,x2) di numeri interi che soddisfano tutti i vincoli del problema.
$$ S = \{ \ (0;2) \ , \ (1;2) \ , \ (2;2) \ , \ (0;1) \ , \ (1;1) \ , \ (2;1) \ , \ (2;0) \ \} $$
Nota. In un problema di programmazione lineare, invece, l'insieme delle soluzioni ammissibili comprende tutti i punti del poligono ABCD.
E così via.
