Rilassamento lineare

Il rilassamento lineare è una tecnica di risoluzione dei problemi di programmazione intera che consiste nel risolvere un problema con la programmazione lineare cercando le soluzioni intere più vicine.

Come funziona

Dato un problema di programmazione intera

1. rimuovo il vincolo di interezza
2. risolvo il problema con la programmazione lineare
3. cerco una soluzione intera tra le soluzioni ammissibili lineari

   Nota. Se il problema non ammette soluzioni lineari allora è sicuro che non esistono nemmeno le soluzioni intere. In questo caso è inutile cercarle. Viceversa, se il problema ammette soluzioni lineari non si può dire nulla. Potrebbero esserci soluzioni intere oppure no.

Nel caso esistano le soluzioni intere sono quasi sempre sub-ottimali rispetto alle soluzioni lineari.

Al massimo una soluzione intera può essere uguale a una soluzione lineare. Mai migliore.

Un esempio pratico

Questo problema include il vincolo di interezza.

$$ min \ z = x_1+x_2 \\ \begin{cases} x_1+2x_2 \ge 4 \\ 3x_1+x_2 \le 11 \\ x_1-x_2 \ge -1 \\ \\ x_1,x_2 \ge 0 \\ x_1,x_2 \in Z \end{cases} $$

Pertanto, si tratta di un problema di programmazione intera.

Per risolverlo rimuovo il vincolo di interezza.

$$ min \ x_1+x_2 \\ \begin{cases} x_1+2x_2 \ge 4 \\ 3x_1+x_2 \le 11 \\ x_1-x_2 \ge -1 \\ \\ x_1,x_2 \ge 0 \end{cases} $$

In questo modo posso trovare le soluzioni ammissibili usando gli algoritmi della programmazione lineare.

Ad esempio, l'algoritmo del simplesso o il metodo grafico.

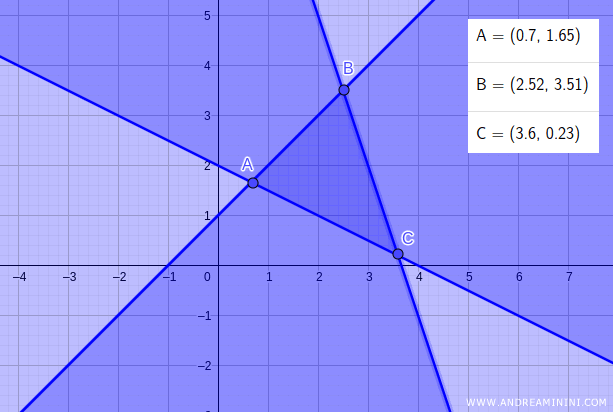
Le soluzioni ammissibili del problema lineare sono comprese nell'area ABC.

In questo caso la soluzione del problema è il punto A(0.7;1.65) ossia x₁=0.7 e x₂=1.65 dove la funzione obiettivo è z_L=2.35

$$ z_L = x_1 + x_2 = 0.7 + 1.65 = 2.35 $$

Una volta trovata la soluzione lineare ottimale A(0.7;1.65) cerco le combinazioni intere più vicine arrotondando per eccesso e per difetto le variabili x₁=0.7 e x₂=1.65

I punti con le coordinate intere più vicine al punto di ottimo lineare sono quattro: (0;1) , (0;2) , (1;1) e (1;2).

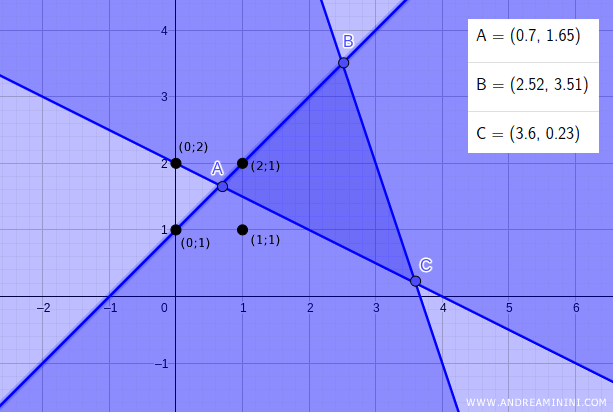
I punti (0;1) , (1;1) e (0;2) posso eliminarli sono soluzioni inammissibili, perché si trovano al di fuori dell'area ABC delle soluzioni ammissibili del problema.

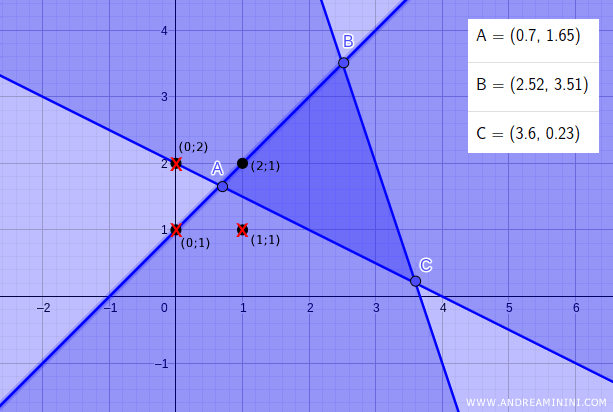
Pertanto, la soluzione intera del problema è il punto (2;1) ossia i valori x₁=1 e x₂=2 dove la funzione obiettivo vale z_i=3.

$$ z_i = x_1 + x_2 = 1 + 2 = 3 $$

Nota. La soluzione intera trovata con il rilassamento lineare z_i è quasi sempre subottimale rispetto alla soluzione lineare z_L o al massimo uguale. Mai migliore. In effetti, in questo esempio la soluzione lineare è z_L=2.34 mentre la soluzione intera e z_i=3. Essendo un problema di minimizzazione della funzione obiettivo z la soluzione intera è subottimale. $$ z_i \ge z_L $$

In questo esempio ho cercato le soluzioni intere usando il metodo dell'arrotondamento.

E' un metodo molto semplice ma ha diversi svantaggi.

• L’arrotondamento per difetto e per eccesso di ogni variabile non intera causa una crescita esponenziale delle combinazioni 2ⁿ al crescere del numero (n) delle variabili del problema.
• Non è detto che la soluzione intera sia una buona approssimazione di quella lineare. La soluzione intera potrebbe esistere ma essere molto diversa oppure mancare del tutto.

Osservazioni

Alcune osservazioni utili sul rilassamento lineare

• Se non esiste una soluzione lineare, allora non esiste nemmeno una soluzione intera
  Le soluzioni intere S_I sono un sottoinsieme delle soluzioni lineari S_L. $$ S_I ⊆ S_L $$ Quindi, se l'insieme delle soluzioni lineari è un insieme vuoto S_L=Ø anche il sottoinsieme delle soluzioni intere deve necessariamente essere un insieme vuoto S_I=Ø. $$ S_L = Ø \Longrightarrow S_I = Ø $$ Non vale però la relazione inversa. Se l'insieme delle soluzioni lineari non è vuoto S_L≠Ø , non posso affermare nulla sul sottoinsieme S_I.
  

  L'esistenza delle soluzioni lineari è una condizione necessaria ma non sufficiente per l'esistenza delle soluzioni intere. Ad esempio un problema potrebbe ammettere un'area di soluzioni lineari ammissibili ABCD che non include punti con coordinate intere.
  
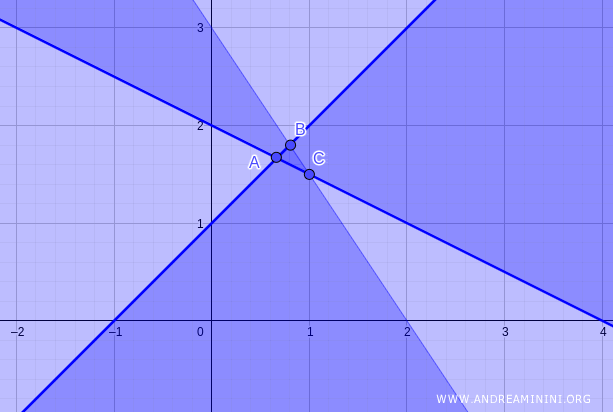
  Se invece non esiste l'area delle soluzioni lineari ammissibili ABC di un problema, allora non possono esistere nemmeno dei singoli punti del piano con coordinate (x₁;x₂) intere che risolvono il problema.

• Se un problema ammette una soluzione lineare allora l'eventuale soluzione intera è uguale o sub-ottimale. Se il rilassamento lineare porta a una soluzione z_L ottimale, la soluzione intera z_i potrebbe non esistere (problema impossibile z_i=∞) essere sub-ottimale (z_i>z_L) oppure coincidere con la soluzione lineare (z_i=z_L).

E così via.