Come riconoscere una formulazione ottimale

Dal punto di vista matematico un poliedro ha tutti i vertici a componenti intere (formulazione razionale) se in un problema in forma standard

• i coefficienti e i termini noti del sistema sono numeri interi
• la matrice dei coefficienti m x n con m≤n ha rango m
• ogni base ha il determinante uguale a ± 1 (base unimodulare)

Svantaggi. Questo metodo è poco pratico dal punto computazionale perché al crescere del numero delle variabili causa un aumento esponenziale delle operazioni di calcolo dei determinanti delle basi.

Esempio

Verifico se questo problema ha tutti i vertici a componenti intere

$$ min \ x_1+x_2 \\ \begin{cases} x_1 + x_2 \le 4 \\ x_1 + x_2 \ge 2 \\ \\ x_1,x_2 \ge 0 \end{cases} $$

Sia i coefficienti che i termini noti del sistema sono numeri interi.

Riscrivo il problema in forma standard

Introduco le variabili di scarto di slack e surplus per eliminare le disequazioni

$$ min \ x_1+x_2 \\ \begin{cases} x_1 + x_2 + x_3 = 4 \\ x_1 + x_2 - x_4 = 2 \\ \\ x_1,x_2,x_3,x_4 \ge 0 \end{cases} $$

Il problema ha m=2 vincoli (equazioni) e n=4 variabili. Quindi, la condizione m<n è soddisfatta.

Scrivo la matrice dei coefficienti A del problema

$$ A = \begin{pmatrix} 1 & 1 & 1 & 0 \\ 1 & 1 & 0 & -1 \end{pmatrix} $$

Il rango della matrice è uguale a 2.

Pertanto, anche la seconda condizione è soddisfatta rank(A)=m

$$ rank(A)=m=2 $$

Verifica. Definisco la matrice su Matlab/Octave e calcolo il rango con la funzione rank().

Per trovare le basi individuo le sottomatrici 2x2 della matrice dei coefficienti scartando quelle con determinante nullo.

$$ \det [A_1 A_2] = \det \begin{pmatrix} 1 & 1 \\ 1 & 1 \end{pmatrix} = 0 \ \ \ \color{red}{scartata} $$

$$ \det [A_1 A_3] = \det \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix} = -1 \ \ \ \ base $$

$$ \det [A_1 A_4] = \det \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} = -1 \ \ \ \ base $$

$$ \det[A_2 A_3] = \det \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix} = -1 \ \ \ \ base $$

$$ \det[A_2 A_4] = \det \begin{pmatrix} 1 & 0 \\ 1 & -1 \end{pmatrix} = -1 \ \ \ \ base $$

$$ \det[A_3 A_4] = \det \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} = -1 \ \ \ \ base $$

Pertanto, le basi sono [A₁ A₃] , [A₁ A₄] , [A₂ A₃] , [A₂ A₄] , [A₃ A₄].

Nota. Con le lettere A₁ A₂ A₃ A₃ indico i vettori colonna della matrice dei coefficienti. Ad esempio A1 è la prima colonna, A2 è la seconda colonna e via dicendo. $$ A_1 = \begin{pmatrix} 1 \\ 1 \end{pmatrix} $$ $$ A_2 = \begin{pmatrix} 1 \\ 1 \end{pmatrix} $$ $$ A_3 = \begin{pmatrix} 1 \\ 0 \end{pmatrix} $$ $$ A_4 = \begin{pmatrix} 0 \\ -1 \end{pmatrix} $$ Quindi, la base [A₁ A₃] si ottiene mettendo i due vettori colonna in una matrice $$ [A_1 A_3] = \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix} $$ E via dicendo.

Tutte le basi hanno determinante -1 o +1. Quindi sono matrici unimodulari.

Pertanto, il problema ha tutti i vertici a componenti intere.

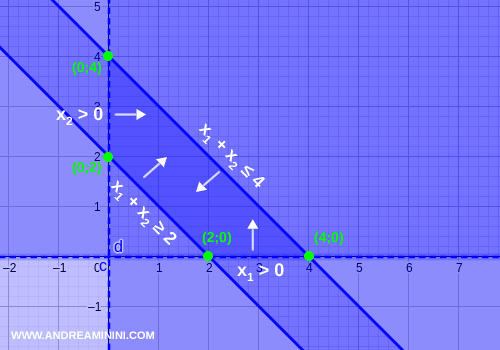
Verifica. Per verificarlo rappresento graficamente il sistema di equazioni lineari sul diagramma cartesiano. Il poliedro ha effettivamente tutti i vertici a componenti intere. I vertici si trovano alle coordinate (0;2), (0;4), (2;0), (4,0)

Sapendo che

$$ A x = b $$

ne consegue che

$$ x = A^{-1} b $$

Sapendo che il vettore dei termini noti del problema è

$$ b = \begin{pmatrix} 4 \\ 2 \end{pmatrix} $$

Sostituisco A con le basi per individuare le soluzioni di base ammissibili (SBA) del problema

Soluzione di base 1

$$ x = A^{-1} b $$

$$ x_{(1 \ 3)} = \begin{pmatrix} x_1 \\ x_3 \end{pmatrix} = [A_1 A_3]^{-1} b = \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix}^{-1} \begin{pmatrix} 4 \\ 2 \end{pmatrix} = \begin{pmatrix} 2 \\ 2 \end{pmatrix} $$

Una soluzione di base è x₁=2 x₂=0 x₃=2 x₄=0 ed è ammissibile perché rispetta i vincoli x₁≥0 e x₂≥0

Individua il vertice alle coordinate (x₁;x₂)=(2;0) del grafico.

Verifica. Sostituisco x₁=2 x₂=0 x₃=2 x₄=0 nel sistema di equazioni lineari $$ \begin{cases} x_1 + x_2 + x_3 = 4 \\ x_1 + x_2 - x_4 = 2 \\ \\ x_1,x_2,x_3,x_4 \ge 0 \end{cases} \begin{cases} 2 + 0 + 2 = 4 \\ 2 + 0 - 0 = 2 \\ \\ x_1,x_2,x_3,x_4 \ge 0 \end{cases} $$ Il sistema è soddisfatto. E' una soluzione di base ammissibile (SBA) del problema.

Soluzione di base 2

$$ x = A^{-1} b $$

$$ x_{(1 \ 4)} = \begin{pmatrix} x_1 \\ x_4 \end{pmatrix} = [A_1 A_4]^{-1} b = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}^{-1} \begin{pmatrix} 4 \\ 2 \end{pmatrix} = \begin{pmatrix} 4 \\ 2 \end{pmatrix} $$

Una soluzione di base è x₁=4 x₂=0 x₃=0 x₄=2 ed è ammissibile perché rispetta i vincoli x₁≥0 e x₂≥0

Individua il vertice alle coordinate (x₁;x₂)=(4;0) del grafico.

Verifica. Sostituisco x₁=4 x₂=0 x₃=0 x₄=2 nel sistema di equazioni lineari $$ \begin{cases} x_1 + x_2 + x_3 = 4 \\ x_1 + x_2 - x_4 = 2 \\ \\ x_1,x_2,x_3,x_4 \ge 0 \end{cases} \begin{cases} 4 + 0 + 0 = 4 \\ 4 + 0 - 2 = 2 \\ \\ x_1,x_2,x_3,x_4 \ge 0 \end{cases} $$ Il sistema è soddisfatto. E' una soluzione di base ammissibile (SBA) del problema.

Soluzione di base 3

$$ x = A^{-1} b $$

$$ x_{(2 \ 3)} = \begin{pmatrix} x_2 \\ x_3 \end{pmatrix} = [A_2 A_3]^{-1} b = \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix}^{-1} \begin{pmatrix} 4 \\ 2 \end{pmatrix} = \begin{pmatrix} 2 \\ 2 \end{pmatrix} $$

Una soluzione di base è x₁=0 x₂=2 x₃=2 x₄=0 ed è ammissibile perché rispetta i vincoli x₁≥0 e x₂≥0

Individua il vertice alle coordinate (x₁;x₂)=(0;2) del grafico.

Verifica. Sostituisco x₁=0 x₂=2 x₃=2 x₄=0 nel sistema di equazioni lineari $$ \begin{cases} x_1 + x_2 + x_3 = 4 \\ x_1 + x_2 - x_4 = 2 \\ \\ x_1,x_2,x_3,x_4 \ge 0 \end{cases} \begin{cases} 0 + 2 + 2 = 4 \\ 0 + 2 - 0 = 2 \\ \\ x_1,x_2,x_3,x_4 \ge 0 \end{cases} $$ Il sistema è soddisfatto. E' una soluzione di base ammissibile (SBA) del problema.

Soluzione di base 4

$$ x = A^{-1} b $$

$$ x_{(2 \ 4)} = \begin{pmatrix} x_2 \\ x_4 \end{pmatrix} = [A_2 A_4]^{-1} b = \begin{pmatrix} 1 & 0 \\ 1 & -1 \end{pmatrix}^{-1} \begin{pmatrix} 4 \\ 2 \end{pmatrix} = \begin{pmatrix} 4 \\ 2 \end{pmatrix} $$

Una soluzione di base è x₁=0 x₂=4 x₃=0 x₄=2 ed è ammissibile perché rispetta i vincoli x₁≥0 e x₂≥0

Individua il vertice alle coordinate (x₁;x₂)=(0;4) del grafico.

Verifica. Sostituisco x₁=0 x₂=4 x₃=0 x₄=2 nel sistema di equazioni lineari $$ \begin{cases} x_1 + x_2 + x_3 = 4 \\ x_1 + x_2 - x_4 = 2 \\ \\ x_1,x_2,x_3,x_4 \ge 0 \end{cases} \begin{cases} 0 + 4 + 0 = 4 \\ 0 + 4 - 2 = 2 \\ \\ x_1,x_2,x_3,x_4 \ge 0 \end{cases} $$ Il sistema è soddisfatto. E' una soluzione di base ammissibile (SBA) del problema.

Soluzione di base 5

$$ x = A^{-1} b $$

$$ x_{(3 \ 4)} = \begin{pmatrix} x_3 \\ x_4 \end{pmatrix} = [A_3 A_4]^{-1} b = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}^{-1} \begin{pmatrix} 4 \\ 2 \end{pmatrix} = \begin{pmatrix} 4 \\ -2 \end{pmatrix} $$

Una soluzione di base è x₁=0 x₂=0 x₃=4 x₄=-2 ma non è ammissibile perché non rispetta il vincolo x₄≥0

E così via.