Formulazione razionale della programmazione intera
La formulazione razionale individua un poliedro nell'area delle soluzioni ammissibili in cui tutti i vertici hanno componenti intere.
A cosa serve
E' una tecnica che mi permette di risolvere un problema di programmazione intera usando gli algoritmi della programmazione lineare.
Come funziona
- Trasformo il problema di programmazione intero in un problema lineare tramite il rilassamento lineare
- Individuo il poliedro P1 dell'area delle soluzioni ammissibili del problema dopo il rilassamento lineare
- Delineo un poliedro P2 più piccolo che contiene tutte le componenti intere dell'area delle soluzioni ammissibili.
Nota. Il poliedro P2 contiene le stesse soluzioni intere del poliedro iniziale P1. Quindi, è del tutto equivalente. Ha però il vantaggio di essere circoscritto in un'area più piccola e avere i vertici con componenti intere. Questo mi permette di trovare una soluzione ottimale usando uno degli algoritmi della programmazione lineare.
Un esempio pratico
Devo risolvere un problema di programmazione intera.
$$ min \ z = x_1+x_2 \\ \begin{cases} x_1+2x_2 \ge 4 \\ 3x_1+x_2 \le 11 \\ x_1-x_2 \ge -1 \\ \\ x_1,x_2 \ge 0 \\ x_1,x_2 \in Z \end{cases} $$
Per risolverlo applico la tecnica del rilassamento lineare rimuovendo il vincolo di interezza.
$$ min \ x_1+x_2 \\ \begin{cases} x_1+2x_2 \ge 4 \\ 3x_1+x_2 \le 11 \\ x_1-x_2 \ge -1 \\ \\ x_1,x_2 \ge 0 \end{cases} $$
In pratica, tratto il problema come se fosse di programmazione lineare.
Questo mi permette di trovare l'area delle soluzioni ammissibili (ABC) del problema in forma lineare.
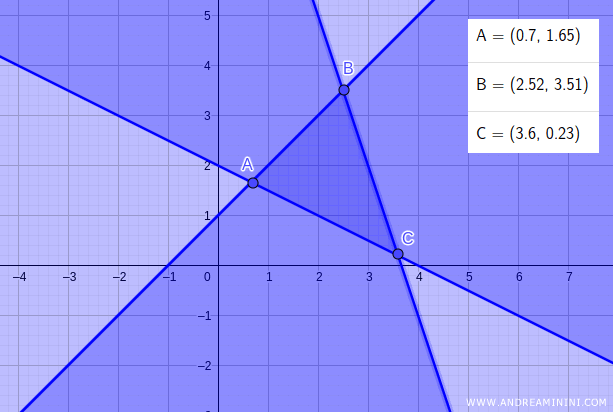
Le soluzioni ammissibili del problema lineare sono comprese nell'area ABC.
Al suo interno sono presenti alcune soluzioni intere (punti neri).

L'area ABC è il poliedro P1 iniziale che ottengo dopo il rilassamento lineare.
Piuttosto che lavorare con l'area ABC, individuo un'area più piccola DEFGH che include tutte le soluzioni intere.

L'area DEFGH individua un secondo poliedro P2 equivalente al primo perché contiene tutte le soluzioni intere del poliedro P1.
Questo secondo poliedro ha però il vantaggio d'essere più piccolo e di avere i vertici con componenti intere.
$$ D(1;2) \\ E(1;3) \\ F(3;2) \\ G(3;1) \\ H(2;1) $$
Sapendo che
- la soluzione ottimale di un problema di programmazione lineare si trova sempre nei vertici del poliedro
- tutti i vertici del poliedro P2 hanno componenti intere
Ne deduco che uno dei vertici del poliedro P2 è la soluzione ottimale del problema di programmazione intera.

In questo caso ci sono due soluzioni ottimali (punti verdi)
- Il vertice D(1;2)
Nel punto D(1;2) le variabili decisionali assumono i valori x1=1 e x2=2. La funzione obiettivo z=x1+x2 del problema è z=3 $$ z = x_1 + x_2 = 1+ 2 = 3 $$ - Il vertice H(2;1)
Nel punto H(2;1) le variabili decisionali assumono i valori x1=2 e x2=1. Anche in questo caso la funzione obiettivo z=x1+x2 del problema è z=3 $$ z = x_1 + x_2 = 2+ 1 = 3 $$
In questo modo ho trovato le soluzioni ottimali del problema di programmazione intera usando uno dei metodi della programmazione lineare.
La differenza tra formulazione razionale e ottimale
La formulazione razionale è un qualsiasi raggruppamento delle soluzioni di un problema lineare in grado di comprendere tutte le soluzioni intere.
Se due formulazioni razionali P1 e P2 comprendono tutte le soluzioni intere, la formulazione razionale più piccola è preferibile perché offre un'approssimazione migliore del problema di programmazione intera.
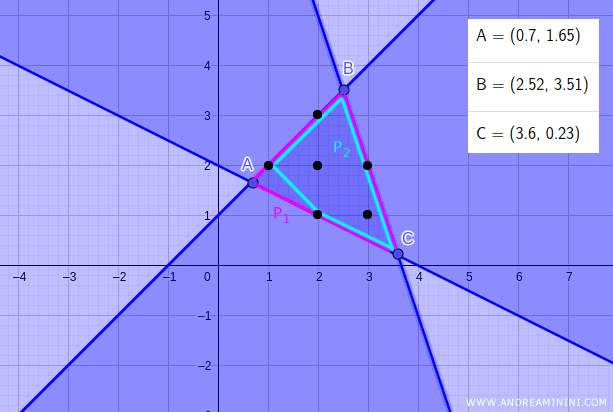
In questo caso P2 è un sottoinsieme di P1, quindi è preferibile.
$$ P_2 ⊆ P_1 $$
Una formulazione razionale è detta formulazione ottimale se non contiene al suo interno altre formulazioni razionali più piccole.
Ad esempio, la formulazione P3 è una formulazione ottimale.

A cosa serve la formulazione ottimale del problema?
Le formulazioni ottimali sono poliedri che hanno tutti i vertici con componenti intere.

Pertanto, la soluzione lineare coincide con la soluzione intera del problema.
Nota. Le soluzioni ottimali del problema lineare si trovano nei vertici del poliedro delle soluzioni ammissibili. Se i vertici hanno tutti le componente intere, la soluzione ottimale lineare è anche una soluzione ottimale intera. Inoltre, se il problema lineare è inammissibile, ossia non ha soluzioni, allora non esistono nemmeno soluzioni intere. E via dicendo.
Questo mi permette di usare i metodi lineari per risolvere i problemi di programmazione intera.
Pro e contro della riformulazione
Vantaggi
La riformulazione del problema mi permette di trovare le soluzioni intere usando gli stessi metodi della programmazione lineare.
E' un approccio semplice ed efficace.
Inoltre, il numero delle variabili del problema resta lo stesso.
Svantaggi
La riformulazione ottimale potrebbe essere molto costosa in termini computazionali perché in alcuni casi il numero dei vincoli del problema cresce in modo esponenziale.
Ad esempio, questo poliedro ha solo 4 vincoli nella programmazione lineare.

Il poliedro ha 4 vertici nessuno dei quali ha componenti intere.
Per riformulare il problema in modo ottimale devo usare 8 vincoli.

Dopo la riformulazione il poliedro ha 8 vertici ognuno dei quali ha componenti intere.
E' un esempio banale ma rende l'idea del problema. Il numero dei vincoli del problema è raddoppiato.
Nota. La riformulazione ottimale è utilizzabile nei casi più semplici e in quelli in cui il poliedro delle soluzioni intere ha una forma semplice. Nei casi in cui le soluzioni intere del problema generano un poliedro con una forma complessa, invece, la riformulazione richiede l'introduzione di molte più disequazioni nel sistema.
E così via.
