L'algoritmo del simplesso rivisto o revisionato
L'algoritmo del simplesso rivisto è una versione dell'algoritmo tradizionale più efficiente che si basa sul calcolo matriciale.
Si parla di versione "rivista" o "revisionata" perché, a parità di risultato, riduce il numero dei calcoli.
Inoltre, è più facile da tradurre in un programma informatico.
Come funziona
L'algoritmo del simplesso si basa sulla matrice di riporto (carry matrix).
$$ \begin{pmatrix} -d-c_B^T A_B^{-1}b & -c_B^T A_B^{-1} \\ A_B^{-1}b & A_B^{-1} \end{pmatrix} $$
Come è composta?
- Il primo elemento in alto a sinistra è il valore della funzione obiettivo.
- Il secondo elemento in alto a destra è il vettore dei coefficienti di costo delle variabili di base.
- Il terzo elemento in basso a sinistra è il vettore dei termini noti (b) delle variabili di base.
- Il quarto elemento in basso a destra è la matrice dei coefficienti tecnici delle variabili di base.
Ogni cambio di base avviene con un'operazione pivot sulla matrice di riporto.
Nota. Nell'algoritmo del simplesso tradizionale ogni operazione pivot modifica tutte le colonne della matrice pivot.
Dopo aver costruito la matrice di riporto, verifico se le variabili fuori base soddisfano le condizioni si ottimalità.
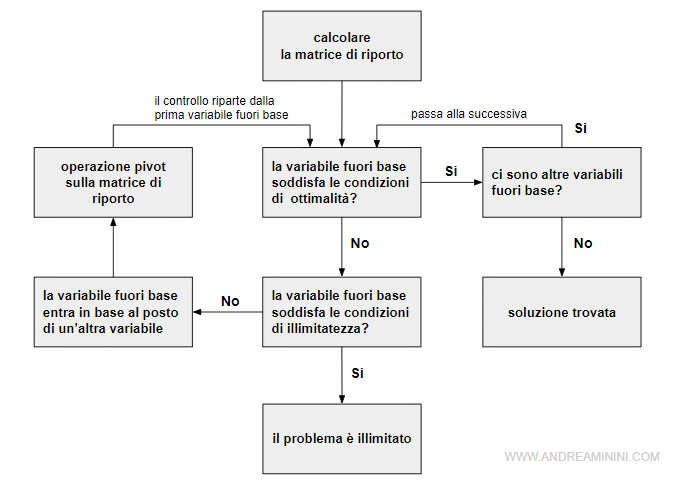
Se le condizioni di ottimalità non sono soddisfatte su una variabile fuori base.
- Verifico se la variabile soddisfa le condizioni di illimitatezza
- Se condizioni di illimitatezza non sono soddisfatte, faccio entrare in base la variabile.
- Aggiorno la matrice di riporto con un'operazione pivot.
Quali sono i vantaggi?
Se una variabile non soddisfa l'ottimalità non devo controllare anche le altre. Verifico subito se soddisfa le condizioni di illimitatezza ed eventualmente la faccio entrare in base al posto di un'altra.
La matrice di riporto viene aggiornata con l'operazione pivot dopo ogni iterazione. Quindi, non devo ricalcolarla daccapo.
Nota. In questo algoritmo non è più necessario calcolare la matrice inversa dei coefficienti di base dopo ogni iterazione. Si calcola soltanto all'inizio. Il che è molto utile. Il calcolo della matrice inversa fa perdere parecchio tempo quando si cerca di risolvere su carta il problema ed è molto facile sbagliarsi.
Un esempio pratico
Devo risolvere questo problema
$$ \min x_1 + 2x_2 - 4x_3 +x_4 - x_6 +2x_7 \\ \begin{cases} x_1 - 2x_2 + x_3 + 4x_6 +x_8 = 10 \\ x_2 - x_3 + x_5 + x_6 + 2x_7 + 4x_8 = 6 \\ 2x_2 + x_3 + x_4 + x_6 + x_7 + x_8 = 4 \\ x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8 \ge 0 \end{cases} $$
E' già in forma standard.
Il vettore dei costi è
$$ c^T = \begin{pmatrix} 1 & 2 & -4 & 1 & 0 & -1 & 2 & 0 \end{pmatrix} $$
La matrice dei coefficienti è
$$ A = \begin{pmatrix} 1 & -2 & 1 & 0 & 0 & 4 & 0 & 1 \\
0 & 1 & -1 & 0 & 1 & 1 & 2 & 4 \\ 0 & 2 & 1 & 1 & 0 & 1 & 1 & 1 \\ \end{pmatrix} $$
Trasformo il modello in forma canonica rispetto alla base B=[1,5,4]
In quanto x1, x5, x4 hanno già coefficienti unitari rispettivamente nel primo, secondo e terzo vincolo.
Inoltre, i tre vettori colonna compongono una matrice identità che agevola i calcoli.
$$ \begin{cases} \min c_B^T A_B^{-1}b + c_N^T x_N \\ x_B = A_B^{-1}b - A_B^{-1} A_N x_N \\ x_B,x_N \ge 0 \end{cases} $$
A questo punto mi basta costruire la matrice di riporto.
$$ \begin{pmatrix} -d-c_B^T A_B^{-1}b & -c_B^T A_B^{-1} \\ A_B^{-1}b & A_B^{-1} \end{pmatrix} $$
La matrice inversa AB-1 della base è
$$ A_B^{-1} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}^{-1} $$
$$ A_B^{-1} = \frac{1}{det(A_B)} \cdot cof(A_b)^T $$
$$ A_B^{-1} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$
Il vettore b è
$$ b = \begin{pmatrix} 10 \\ 6 \\ 4 \end{pmatrix} $$
Il vettore dei costi delle variabili di base è
$$ c_B^T = ( 1, 0, 1 ) $$
Svolgo i calcoli nel primo elemento in alto a sinistra della matrice di riporto
Sapendo che d=0 in quanto nella funzione obiettivo non c'è nessun valore .
$$ \begin{pmatrix} -d-c_B^T A_B^{-1}b & -c_B^T A_B^{-1} \\ A_B^{-1}b & A_B^{-1} \end{pmatrix} $$
$$ \begin{pmatrix} -0-(1, 0, 1) \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 10 \\ 6 \\ 4 \end{pmatrix} & -c_B^T A_B^{-1} \\ A_B^{-1}b & A_B^{-1} \end{pmatrix} $$
$$ \begin{pmatrix} -0-(1, 0, 1) \cdot \begin{pmatrix} 10 \\ 6 \\ 4 \end{pmatrix} & -c_B^T A_B^{-1} \\ A_B^{-1}b & A_B^{-1} \end{pmatrix} $$
$$ \begin{pmatrix} -14 & -c_B^T A_B^{-1} \\ A_B^{-1}b & A_B^{-1} \end{pmatrix} $$
Quindi il valore della funzione obiettivo è -14
Svolgo i calcoli nel secondo elemento in alto a destra
$$ \begin{pmatrix} -14 & -(1, 0, 1) \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \\ A_B^{-1}b & A_B^{-1} \end{pmatrix} $$
$$ \begin{pmatrix} -14 & \begin{pmatrix} -1 &0 & -1 \end{pmatrix} \\ A_B^{-1}b & A_B^{-1} \end{pmatrix} $$
Svolgo i calcoli nel terzo elemento in basso a sinistra.
In questo caso il vettore dei termini noti va calcolato con la base attuale b'=AB-1b
$$ \begin{pmatrix} -14 & \begin{pmatrix} -1 & 0 & -1 \end{pmatrix} \\ \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 10 \\ 6 \\ 4 \end{pmatrix} & A_B^{-1} \end{pmatrix} $$
$$ \begin{pmatrix} -14 & \begin{pmatrix} -1 & 0 & -1 \end{pmatrix} \\ \begin{pmatrix} 10 \\ 6 \\ 4 \end{pmatrix} & A_B^{-1} \end{pmatrix} $$
Svolgo i calcoli nell'ultimo elemento in basso a destra.
Si tratta di copiare la matrice inversa delle variabili di base AB-1.
$$ \begin{pmatrix} -14 & \begin{pmatrix} -1 & 0 & -1 \end{pmatrix} \\ \begin{pmatrix} 10 \\ 6 \\ 4 \end{pmatrix} & \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \end{pmatrix} $$
La prima matrice di riporto è pronta per essere elaborata
$$ C^{0} = \begin{pmatrix} -14 & -1 & 0 & -1 \\ 10 & 1 & 0 & 0 \\ 6 & 0 & 1 & 0 \\ 4 & 0 & 0 & 1 \end{pmatrix} $$
Iterazione 1
Una volta costruita la matrice di riporto l'algoritmo verifica se sono soddisfatte le condizioni di ottimalità in ogni variabile fuori base (x2, x3, x6, x7, x8).
$$ c_j ^{0} = c_j - (c_B^T A_B^{-1})^{(0)} A_j \ge 0 $$
Dove cj è il coefficiente di costo iniziale della variabile fuori base, mentre (cBTAB-1)(0) sono i coefficienti di costo delle variabili di base nella matrice di riporto corrente.
Il vettore Aj è invece il vettore dei coefficienti tecnici iniziali della variabili fuori base.
La prima variabile fuori base è x2 ossia j=2.
$$ c_2 ^{(0)} = c_2 - (c_B^T A_B^{-1})^{(0)} A_2 \ge 0 $$
$$ c_2 ^{(0)} = 2 - (1 , 0 , 1 ) \begin{pmatrix} -2 \\ 1 \\ 2 \end{pmatrix} \ge 0 $$
$$ c_2 ^{(0)} = 2 \ge 0 $$
Soddisfa la condizione di ottimalità, quindi passo alla successiva.
La seconda variabile fuori base è x3 ossia j=3.
$$ c_3 ^{(0)} = c_3 - (c_B^T A_B^{-1})^{(0)} A_3 \ge 0 $$
$$ c_3 ^{(0)} = -4 - (1 , 0 , 1 ) \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \ge 0 $$
$$ c_3 ^{(0)} = -5 \ge 0 $$
La condizione di ottimalità non è soddisfatta dalla variabile x3.
Pertanto, è inutile controllare anche le restanti variabili fuori base.
Considero la variabile x3 come variabile in entrata nella base ossia k=3.
A questo punto verifico se la variabile x3 soddisfa le due condizioni di illimitatezza.
$$ A^{-1}_B \cdot A_k \le 0 \:\:\: con \:\: c_k^{(0)} < 0 $$
ossia
$$ A^{-1}_B \cdot A_3 \le 0 \:\:\: con \:\: c_3^{(0)} < 0 $$
Il coefficiente di costo c3(0)=-5<0. Quindi, una condizione è soddisfatta.
Tuttavia i nuovi coefficienti tecnici di x3 non sono tutti nulli o negativi. Ci sono ancora valori positivi.
$$ A^{(0)}_3 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} \le 0 \:\:\: con \:\: c_3 < 0 $$
$$ A^{(0)}_3 = \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} \le 0 \:\:\: con \:\: c_3 < 0 $$
Quindi, le condizioni di illimitatezza non sono soddisfatte.
Devo decidere quale variabile esce dalla base.
Per farlo applico la regola del minimo rapporto b/a analizzando i nuovi coefficienti positivi di x3 ossia A(0)3 rispetto al vettore b(0).
$$ h = arg \min [ \frac{ \bar{b^{(0)}} }{ \bar{A^{(0)}_k} } ] \:\: con \:\: A^{(0)}_k > 0 $$
$$ h = arg \min [ \frac{10}{1} , - , \frac{ 4 }{ 1} ] $$
$$ h = 3 $$
Esce la terza equazione dalla base b=[1,5,4], quella che definisce la variabile x4.
Ricapitolando, con un'operazione pivot entra in base la variabile x3 al posto di x4.
Nella matrice di riporto aggiungo un orlo a sinistra dove inserisco i dati della variabile entrante x3.
$$ C^{(1)} = \begin{pmatrix} c_3^{(0)} & 14 & -1 & 0 & -1 \\ A^{(0)}_{1,3} & 10 & 1 & 0 & 0 \\ A^{(0)}_{2,3} &6 & 0 & 1 & 0 \\ A^{(0)}_{3,3} & 4 & 0 & 0 & 1 \end{pmatrix} $$
$$ C^{(1)} = \begin{pmatrix} -5 & 14 & -1 & 0 & -1 \\ 1 & 10 & 1 & 0 & 0 \\ -1 &6 & 0 & 1 & 0 \\ 1 & 4 & 0 & 0 & 1 \end{pmatrix} $$
Essendo h=3 e k=3 l'elemento pivot è il primo elemento nella riga h=3 della matrice orlata.
Lo indico tra due simboli <>
$$ C^{(1)} = \begin{pmatrix} -5 & 14 & -1 & 0 & -1 \\ 1 & 10 & 1 & 0 & 0 \\ -1 &6 & 0 & 1 & 0 \\ <1> & 4 & 0 & 0 & 1 \end{pmatrix} $$
Ora calcolo l'operazione pivot sull'elemento pivot <1> sulla colonna orlata (la prima).
Divido la riga pivot (h=3) per l'elemento pivot <1>
$$ C^{(1)} = \begin{pmatrix} -5 & 14 & -1 & 0 & -1 \\ 1 & 10 & 1 & 0 & 0 \\ -1 &6 & 0 & 1 & 0 \\ \frac{1}{1} & \frac{4}{1} & \frac{0}{1} & \frac{0}{1} & \frac{1}{1} \end{pmatrix} $$
$$ C^{(1)} = \begin{pmatrix} -5 & 14 & -1 & 0 & -1 \\ 1 & 10 & 1 & 0 & 0 \\ -1 &6 & 0 & 1 & 0 \\ 1 & 4 & 0 & 0 & 1 \end{pmatrix} $$
Poi modifico le altre righe completando l'operazione pivot
Riga 0
$$ [-5 \:\: 14 \:\: -1 \:\ 0 \:\: -1 ] - (-5) [1 \:\: 4 \:\: 0 \:\ 0 \:\: -1 ] $$
$$ [-5 \:\: 14 \:\: -1 \:\ 0 \:\: -1 ] - [-5 \:\: -20 \:\: 0 \:\ 0 \:\: 5 ] $$
$$ [0 \:\: 34 \:\: -1 \:\ 0 \:\: -6 ] $$
Riga 1
$$ [1 \:\: 10 \:\: 1 \:\ 0 \:\: 0 ] - (1) [1 \:\: 4 \:\: 0 \:\ 0 \:\: -1 ] $$
$$ [1 \:\: 10 \:\: 1 \:\ 0 \:\: 0 ] - [1 \:\: 4 \:\: 0 \:\ 0 \:\: -1 ] $$
$$ [0 \:\: 6 \:\: 1 \:\ 0 \:\: 1 ] $$
Riga 2
$$ [-1 \:\: 6 \:\: 0 \:\ 1 \:\: 0 ] - (-1) [1 \:\: 4 \:\: 0 \:\ 0 \:\: -1 ] $$
$$ [-1 \:\: 6 \:\: 0 \:\ 1 \:\: 0 ] - [-1 \:\: -4 \:\: 0 \:\ 0 \:\: 1 ] $$
$$ [0 \:\: 10 \:\: 0 \:\ 1 \:\: -1 ] $$
Riga 3
E' la riga dell'elemento pivot. Quindi non si modifica.
La matrice orlata dopo l'operazione pivot è la seguente
$$ C^{(1)} = \begin{pmatrix} 0 & 34 & -1 & 0 & -6 \\ 0 & 6 & 1 & 0 & 1 \\ 0 & 10 & 0 & 1 & -1 \\ 1 & 4 & 0 & 0 & 1 \end{pmatrix} $$
Elimino la prima colonna orlata
$$ C^{(1)} = \begin{pmatrix} 34 & -1 & 0 & -6 \\ 6 & 1 & 0 & 1 \\ 10 & 0 & 1 & -1 \\ 4 & 0 & 0 & 1 \end{pmatrix} $$
La matrice di riporto è pronta per la seconda iterazione sulla base B=[1,5,3].
Iterazione 2
Ora la base è [1,5,3].
La matrice di riporto è
$$ C^{(1)} = \begin{pmatrix} 34 & -1 & 0 & -6 \\ 6 & 1 & 0 & 1 \\ 10 & 0 & 1 & -1 \\ 4 & 0 & 0 & 1 \end{pmatrix} $$
Analizzo i costi delle variabili fuori base.
$$ c_j ^{(1)} = c_j - (c_B^T A_B^{-1})^{(0)} A_j \ge 0 $$
La prima variabile fuori base è x2 ossia j=2.
$$ c_2 ^{(1)} = c_2 - (c_B^T A_B^{-1})^{(0)} A_2 \ge 0 $$
$$ c_2 ^{(1)} = 2 - (-1 , 0 , -6 ) \begin{pmatrix} -2 \\ 1 \\ 2 \end{pmatrix} \ge 0 $$
$$ c_2 ^{(1)} = 12 \ge 0 $$
Soddisfa la condizione di ottimalità, quindi passo alla successiva.
La seconda variabile fuori base è x3 ossia j=3.
$$ c_3 ^{(1)} = c_3 - (c_B^T A_B^{-1})^{(0)} A_3 \ge 0 $$
$$ c_3 ^{(1)} = -4 - (-1 , 0 , -6 ) \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} \ge 0 $$
$$ c_3 ^{(1)} = -4 - (-7 ) = 3 \ge 0 $$
Soddisfa la condizione di ottimalità, quindi passo alla successiva.
La terza variabile fuori base è x4 ossia j=4.
$$ c_4 ^{(1)} = c_4 - (c_B^T A_B^{-1})^{(0)} A_4 \ge 0 $$
$$ c_4 ^{(1)} = 1 - (-1 , 0 , -6 ) \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \ge 0 $$
$$ c_4 ^{(1)} = 1 - (-6 ) = 7 \ge 0 $$
Soddisfa la condizione di ottimalità, quindi passo alla successiva.
La quarta variabile fuori base è x6 ossia j=6.
$$ c_6 ^{(1)} = c_4 - (c_B^T A_B^{-1})^{(0)} A_6 \ge 0 $$
$$ c_6 ^{(1)} = -1 - (-1 , 0 , -6 ) \begin{pmatrix} 4 \\ 1 \\ 1 \end{pmatrix} \ge 0 $$
$$ c_6 ^{(1)} = -1 - (-10 ) = 9 \ge 0 $$
Soddisfa la condizione di ottimalità, quindi passo alla successiva.
La quinta variabile fuori base è x7 ossia j=7.
$$ c_7 ^{(1)} = c_7 - (c_B^T A_B^{-1})^{(0)} A_7 \ge 0 $$
$$ c_7 ^{(1)} = 2 - (-1 , 0 , -6 ) \begin{pmatrix} 0 \\ 2 \\ 1 \end{pmatrix} \ge 0 $$
$$ c_7 ^{(1)} = 2 - (-6 ) = 8 \ge 0 $$
Soddisfa la condizione di ottimalità, quindi passo alla successiva.
La sesta variabile fuori base è x8 ossia j=8.
$$ c_8 ^{(1)} = c_8 - (c_B^T A_B^{-1})^{(0)} A_8 \ge 0 $$
$$ c_8 ^{(1)} = 0 - (-1 , 0 , -6 ) \begin{pmatrix} 1 \\ 4 \\ 1 \end{pmatrix} \ge 0 $$
$$ c_8 ^{(1)} = 0 - (-7 ) = 7 \ge 0 $$
Soddisfa la condizione di ottimalità.
Tutte le variabili fuori base soddisfano la condizione di ottimalità.
Pertanto, la soluzione ottimale è
$$ X = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \\ x_6 \\ x_7 \\ x_8 \end{pmatrix} = \begin{pmatrix} 6 \\ 0 \\ 4 \\ 0 \\ 10 \\ 0 \\ 0 \\ 0 \end{pmatrix} $$
E così via.
