Le soluzioni del problema di ottimizzazione
Nella programmazione lineare le soluzioni di un problema di ottimizzazione formano un insieme detto regione ammissibile.
La regione ammissibile è un poliedro P nello spazio.
Se la funzione obiettivo è la minimizzazione dei costi
$$ \min_{ \forall x \in P} f(x) = c^T x $$
Tra le soluzioni della regione ammissibile P potrebbe esserci una soluzione ottimale x*.
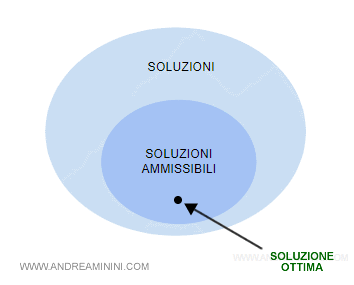
Cos'è una soluzione ottima
Una soluzione ottima del problema è un punto x* di P, tale che
$$ c^Tx* \le c^Tx \:\:\:\text{ per ogni } x \in P$$
Un esempio pratico
Ho un problema di ottimizzazione con la seguente funzione obiettivo
$$ \min z(x) = x_1 + 2x_2 $$
I vincoli del problema sono
$$ \begin{cases} 6x_1+8x_2 \le 30 \\ -2x_1+3x_2 \le 6 \\ x_1+4x_2 \ge 4 \\ x_1 \ge 0 \\ x_2 \ge 0 \end{cases} $$
Rappresento il modello di ottimizzazione nella spazio cartesiano.
Questo mi permette di individuare geometricamente la regione ammissibile delle soluzioni.
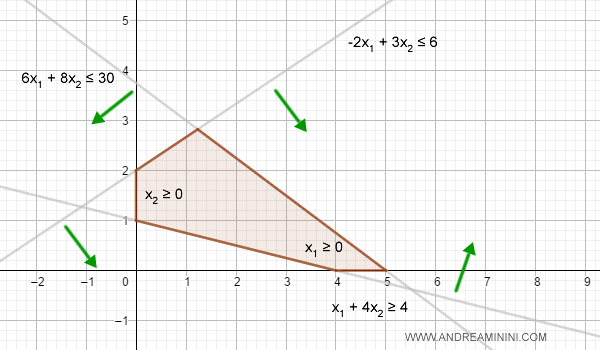
Nota. Se la regione ammissibile non esiste, l'insieme delle soluzioni è vuoto ( P=ø ) e il problema è inammissibile. In questo caso si scrive z*=+∞.
Come trovare la soluzione?
Posso risolvere il sistema lineare oppure trovare la soluzione geometricamente.
Sul diagramma cartesiano aggiungo il gradiente dei costi.
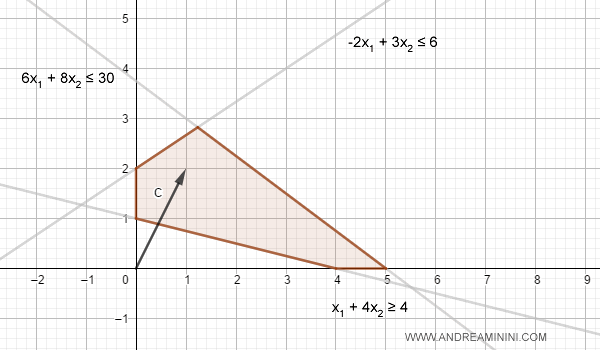
Il gradiente è un vettore con le coordinate del vettore dei costi cT. $$ c = \begin{pmatrix} 1 \\ 2 \end{pmatrix} \\ c^T = ( 1 , 2 ) $$
La soluzione al problema è il punto x* del poliedro P con valore z(x) più basso che si trova sulla retta ortogonale al gradiente.
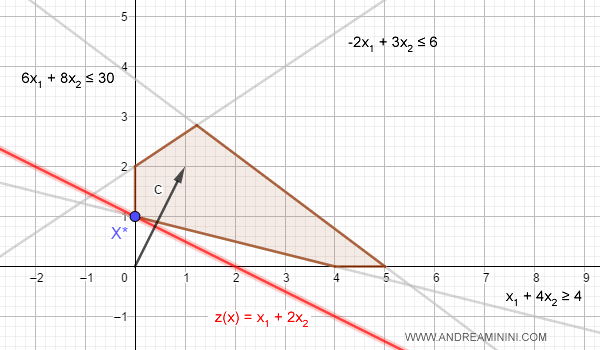
Nota. Se la regione ammissibile esiste ma non è possibile individuare un punto ottimale x*, il problema è illimitato inferiormente. Per ogni soluzione ammissibile x∈P c'è sempre un'altra soluzione migliore. In questo caso non esiste una soluzione ottima x* e si scrive z*=-∞.
Il problema di ottimizzazione in forma standard
- Un problema di ottimizzazione è in forma standard
- se la funzione obiettivo è una funzione min().
- se il poliedro P delle soluzioni è un poliedro in forma standard e non è vuoto.
Esempio
Il precedente sistema
$$ \begin{cases} \min z(x) = x_1 + 2x_2 \\ \\ 6x_1+8x_2 \le 30 \\ -2x_1+3x_2 \le 6 \\ x_1+4x_2 \ge 4 \\ \\ x_1 , x_2 \ge 0 \end{cases} $$
in forma standard diventa
$$ \begin{cases} \min z(x) = x_1 + 2x_2 \\ \\ 6x_1+8x_2 +x_3 = 30 \\ -2x_1+3x_2 +x_4 = 6 \\ x_1+4x_2 -x_5 = 4 \\ \\ x_1, x_2, x_3,x_4,x_5 \ge 0 \end{cases} $$
Perché usare la forma standard?
La forma standard aggiunge alcune proprietà geometriche molto utili per cercare la soluzione di un problema di ottimizzazione.
-
Se la direzione d del poliedro implica cTd < 0, il problema è illimitato inferiormente.
Un problema è illimitato inferiormente se non ammette una soluzione ottima perché per ogni soluzione c'è sempre un'altra soluzione migliore. Ecco un esempio pratico.
Le soluzioni di base e i vertici del poliedro
Dal punto di vista geometrico le soluzioni si trovano ai vertici del poliedro. Queste soluzioni sono dette soluzioni di base.
Non tutte le soluzioni di base sono però valide.
Tra queste occorre selezionare le soluzioni di base ammissibili (SBA) e scartare quelle non ammissibili.
