Il problema illimitato inferiormente

Nella ricerca operativa un problema di ottimizzazione è illimitato inferiormente se per ogni punto x della regione delle soluzioni ammissibili ( poliedro P ) esiste sempre un altro punto x' migliore. $$ c^Tx' < x^Tx $$

Nei problemi illimitati inferiormente non c'è una soluzione ottima.

La funzione di costo f=c^Tx è sempre migliorabile.

Quando una funzione di costo è illimitata inferiormente si scrive

$$ f*=-∞ $$

Come capire se un problema è illimitato inferiormente

Se un problema è illimitato inferiormente il prodotto tra il gradiente dei costi cT e la direzione d del poliedro è inferiore a zero. $$ c^T d < 0 $$

Un esempio pratico

Ho il seguente problema

$$ \begin{cases} \min f(x) = x_1-2x_2 \\ \\ -6x_1+2x_2 \le 6 \\ x_1-2x_2 \le 4 \\ 4x_1 + 16x_2 \ge 25 \\ \\ x_1,x_2 \ge 0 \end{cases} $$

Calcolo il gradiente dei costi ossia il vettore c.

$$ c=\begin{pmatrix} 1 \\ -2 \end{pmatrix} $$

Poi rappresento il vettore c e la regione delle soluzioni ammissibili ( poliedro P ) sugli assi cartesiani.

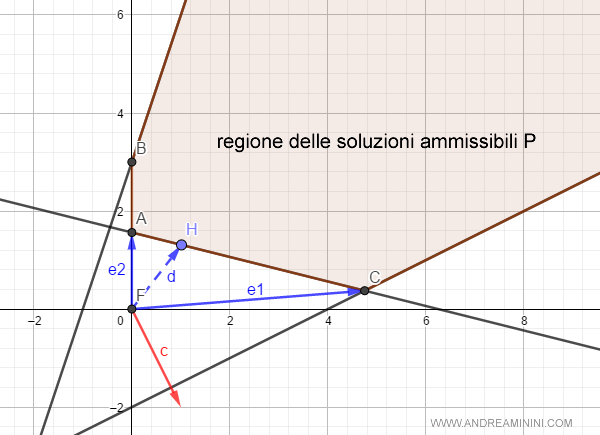
Grazie alla rappresentazione posso individuare gli estremi e₁ e e₂ della direzione.

Scelgo una direzione qualsiasi tra i due estremi.

$$ OH = \begin{pmatrix} 2,27 \\ 1 \end{pmatrix} $$

Poi trasformo il vettore OH in un versore.

Per calcolare il versore devo dividere il vettore per la sua norma euclidea.

$$ d = \frac{OH}{||OH||} = \frac{ \begin{pmatrix} 1 \\ 1,31 \end{pmatrix} }{ \sqrt{1^2+1,31^2} } = \frac{ \begin{pmatrix} 1 \\ 1,31 \end{pmatrix} }{ \sqrt{1,7161} } = \begin{pmatrix} \frac{1}{\sqrt{1,7161}} \\ \frac{1,31}{\sqrt{1,7161}} \end{pmatrix} $$

Infine, calcolo il prodotto tra il vettore dei costi e la direzione.

$$ c^T \cdot = \begin{pmatrix} 1 \\ -2 \end{pmatrix}^T \cdot \begin{pmatrix} \frac{1}{\sqrt{1,7161}} \\ \frac{1,31}{\sqrt{1,7161}} \end{pmatrix} = ( 1 , -2 ) \cdot \begin{pmatrix} \frac{1}{\sqrt{1,7161}} \\ \frac{1,31}{\sqrt{1,7161}} \end{pmatrix} $$

$$ = 1 \cdot \frac{1}{\sqrt{1,7161}} -2 \cdot \frac{1,31}{\sqrt{1,7161}} $$

$$ = \frac{-1,62}{\sqrt{1,7161}} \le 0 $$

Il risultato è minore di zero.

Pertanto, il problema è illimitato inferiormente.

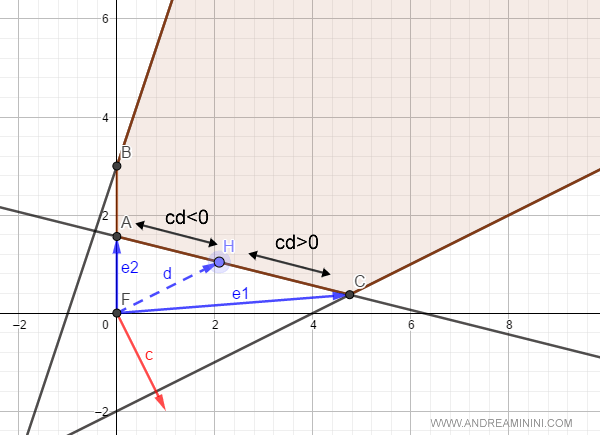
Attenzione. Scegliendo un'altra direzione potrei ottenere anche un risultato positivo. Un problema è illimitato inferiormente se esiste almeno una direzione tale da rendere c^Td<0. E' quindi consigliabile provare entrambe le direzioni vicine agli estremi.

Teorema di illimitatezza

Secondo il teorema di illimitatezza, un problema è illimitato inferiormente se una delle variabili x_N escluse dalla base soddisfa le seguenti condizioni $$ \overline{c_k} \le 0 \\ \overline{A_k} \le 0 $$

Esempio

Un problema di ottimizzazione ha il seguente modello

$$ \begin{cases} \min f(x) = x_1-2x_2 \\ \\ -6x_1+2x_2 \le 6 \\ x_1-2x_2 \le 4 \\ 4x_1 + 16x_2 \ge 25 \\ \\ x_1,x_2 \ge 0 \end{cases} $$

Lo trasformo in forma standard

$$ \begin{cases} \min f(x) = x_1-2x_2 \\ \\ -6x_1+2x_2 +x_3 = 6 \\ x_1-2x_2 + x_4 = 4 \\ 4x_1 + 16x_2 - x_5 = 25 \\ \\ x_1,x_2,x_3,x_4,x_5 \ge 0 \end{cases} $$

Posso esprimere i vincoli in forma matriciale

$$ Ax=b $$ $$ \begin{pmatrix} -6 & 2 & 1 & 0 & 0 \\ 1 & -2 & 0 & 1 & 0 \\ 4 & 16 & 0 & 0 & -1 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{pmatrix} = \begin{pmatrix} 6 \\ 4 \\ 25 \end{pmatrix}$$

Il rango A è uguale al rango A|B.

$$ r(A) = r(A|B) = 3 $$

Secondo il teorema di Rouché-Cappelli il sistema ammette soluzioni.

La matrice ha 5 vettori in colonna, ne selezioni 3 per analizzare una base.

Ad esempio, prendo la combinazione [1,2,3] ossia il primo, il secondo e il terzo vettore della matrice A.

$$ A = [ A_B , A_N ] = [ \begin{pmatrix} -6 & 2 & 1 \\ 1 & -2 & 0 \\ 4 & 16 & 0 \end{pmatrix} , \begin{pmatrix} 0 & 0 \\ 1 & 0 \\ 0 & -1 \end{pmatrix} ] $$

I vettori esclusi x_N sono due. La quarta e la quinta colonna.

Il costo ridotto del quarto vettore (k=4) è

$$ \overline{c_4} = c_4 - c_B^T A_B^{-1}A_k $$

$$ \overline{c_4} = 0 - ( 1, -2, 0 ) A_B^{-1}\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} $$

$$ \overline{c_4} = 0 - ( 1, -2, 0 ) \begin{pmatrix} 0 & 0,67 & 0,08 \\ 0 & -0,17 & 0,04 \\ 1 & 4,33 & 0,42 \end{pmatrix}\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} $$

$$ \overline{c_4} = 0 - ( 1, -2, 0 ) \begin{pmatrix} 0,67 \\ -0,17 \\ 4,33 \end{pmatrix} $$

$$ \overline{c_4} = 0 - ( 1 \cdot 0,67 -2 \cdot ( - 0,17) + 0 \cdot 4,33 )$$

$$ \overline{c_4} = 0 - ( 1,01 )$$

$$ \overline{c_4} = - 1,01 \le 0 $$

Il costo ridotto della variabile è minore di zero.

Ora verifico l'altra condizione di illimitatezza.

$$ \overline{A_k} = A_B^{-1} A_k $$

$$ \overline{A_k} = A_B^{-1} \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} $$

$$ \overline{A_k} = \begin{pmatrix} 0 & 0,67 & 0,08 \\ 0 & -0,17 & 0,04 \\ 1 & 4,33 & 0,42 \end{pmatrix} \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} $$

$$ \overline{A_k} = \begin{pmatrix} 0,67 \\ -0,17 \\ 4,33 \end{pmatrix} $$

Un elemento di A_K è minore di zero.

Quindi, il problema è illimitato inferiormente.