Come costruire un modello nella ricerca operativa
La modellizzazione è la fase in cui si trasforma un problema reale in un modello matematico. In genere, il modello è un sistema con N equazioni / disequazioni e M variabili.
Le variabili del problema
Come prima cosa bisogna individuare tutte le grandezze del problema.
A ogni grandezza si assegna il nome di una variabile.
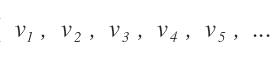
Poi si suddividono le variabili in due gruppi:
- Dati. Sono le variabili del sistema che il decisore non può modificare. Sono fuori dal suo controllo diretto.
- Grandezze decisionali. Sono le variabili che il decisore può controllare e modificare con le sue azioni e decisioni. A loro volta le grandezze decisionali sono classificate in:
- Parametri decisionali. Il valore dei parametri decisionali dipende direttamente dalle azioni del decisore.
- Variabili decisionali. Il valore delle variabili decisionali dipende indirettamente dalle azioni del decisore, è determinato dall'effetto delle azioni sul modello matematico.
I vincoli strutturali del problema
Le variabili non sono indipendenti. Ogni variabile è legata a dei vincoli a seconda della struttura del problema.
Esempio. La variabile Q indica le quantità prodotte da una fabbrica in un giorno. Quindi, la variabile Q può assumere un valore minimo pari a zero e un valore massimo X pari alla capacità produttiva degli impianti della fabbrica.
Le decisioni, gli obiettivi e le preferenze del decision maker
Il decision maker può prendere diverse decisioni.
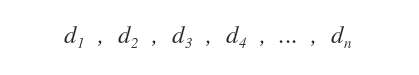
Le decisioni non sono tutte uguali, perché hanno un impatto diverso sulle variabili del sistema.
Per trovarle bisogna individuare gli obiettivi del decisore.
Gli obiettivi sono ordinati secondo le preferenze del decision maker.
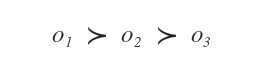
In genere gli obiettivi sono funzioni matematiche f(x) da massimizzare o minimizzare.
Possono essere in funzione di tutte le decisioni o soltanto di alcune.
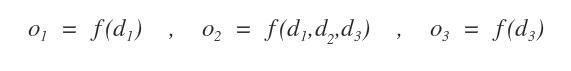
Nota. Gli obiettivi sono altre grandezze del problema che si aggiungono alle variabili del sistema.
In base all'impatto delle decisioni ( d ) sugli obiettivi ( o ), si possono ordinare le decisioni secondo delle relazioni di preferenza.
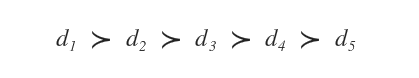
Così facendo è possibile stabile l'ordine di preferenza sia degli obiettivi e sia delle decisioni del decision maker.
Nota. Le preferenze sono soggettive perché dipendono dal decisore. Tuttavia, si possono individuare anche delle relazioni oggettive stabilendo degli assiomi. Ad esempio, ogni agente razionale massimizza la propria utilità. E' infatti irrazionale che faccia del male a se stesso.
A cosa servono le preferenze?
Alcuni obiettivi sono compatibili tra loro e si possono raggiungere contemporaneamente, mentre altri sono conflittuali. L'uno esclude l'altro.
Se gli obiettivi sono conflittuali, il decisore è costretto a sceglierne uno, sacrificando l'altro.
L'ordine delle preferenze consente di stabilire razionalmente quale sarà la sua decisione.
Nota. Dinnanzi a una scelta tra due obiettivi alternativi e conflittuali, un agente razionale sceglie sempre l'obiettivo preferito.
Le preferenze aggiungono nuovi vincoli al sistema matematico.
Sono detti vincoli flessibili perché dipendono dalle scelte del decision maker.
Nota. I vincoli flessibili si distinguono dai vincoli strutturali. I vincoli strutturali sono oggettivi e dipendono dalla natura del problema. I vincoli flessibili, invece, derivano dalle preferenze soggettive del decisore.
Le soluzioni del problema
Una volta costruito il modello matematico, si può cercare la soluzione del problema.
Cos'è una soluzione?
Una soluzione è un vettore di valori da assegnare ai parametri decisionali, nel rispetto dei vincoli strutturali e flessibili del sistema.
A loro volta, i parametri decisionali determinano i valori delle variabili decisionali.
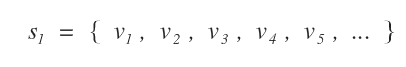
In genere, ogni problema ha molte soluzioni.
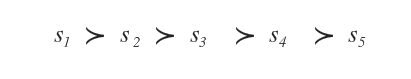
La soluzione ottima è la combinazione di valori che permette di raggiungere gli obiettivi del decisore in modo più efficace ed efficiente ( es. s1 ).
Esempio. Se l'obiettivo dell'impresa è la massimizzazione del profitto, la scelta ottimale è quella che permette di raggiungere il profitto più alto.
A volte non è possibile la decisione ottimale, se il calcolo richiede troppo tempo ( inefficacia ) e costi eccessivi ( inefficienza ).
In questi casi è sufficiente trovare una o più soluzioni accettabili.
Una soluzione è accettabile se raggiunge gli obiettivi in modo soddisfacente ( es. s2 ), senza però avere la certezza che sia la scelta migliore possibile.
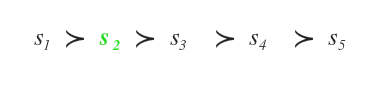
E' una soluzione presa in condizioni di approssimazione e incertezza.
Quali sono i vantaggi delle scelte accettabili?
Le scelte accettabili hanno il vantaggio d'essere trovate in tempi più rapidi e a costi più contenuti rispetto alle scelte ottimali.
Inoltre, le scelte accettabili sono più realistiche, perché si avvicinano di più al comportamento delle persone nel mondo reale.
Esempio. Un consumatore non può calcolare esattamente l'utilità che potrebbe ottenere da tutti i prodotti, perché non ha tutte le informazioni a disposizione e la ricerca diventerebbe troppo costosa. E' quindi portato a scegliere razionalmente il prodott che lo rassicura maggiormente, senza avere la certezza che sia la scelta migliore possibile. E' una scelta "razionalmente emotiva". Per questa ragione la pubblicità è efficace.
La validazione del modello
L'ultima fase della progettazione è la verifica del modello.
Il modello deve essere applicato nel mondo reale per poterne analizzare i feed-back.
Il modello della ricerca operativa è valido soltanto se la soluzione risolve il problema reale.
Se non lo risolve, bisogna ricominciare tutto daccapo.
