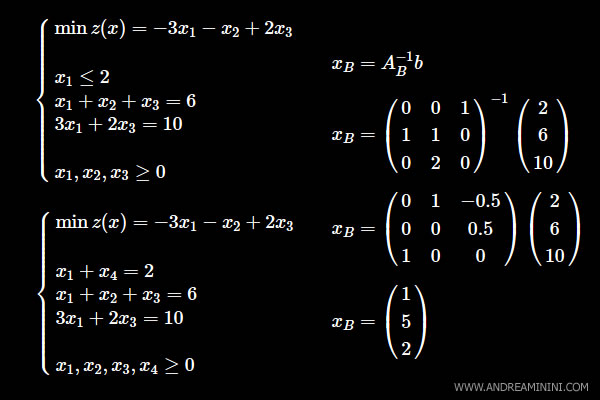Algoritmo del simplesso
Cos'è l'algoritmo del simplesso
L'algoritmo del simplesso è un metodo della programmazione lineare (PL) usato nella ricerca operativa per trovare le soluzioni a un problema di ottimizzazione. E' stato ideato da George Dantzig nel 1947.
Cos'è il simplesso? Il simplesso è un politopo di N+1 vertici in N dimensioni. E' la rappresentazione geometrica su più dimensioni di un problema di ottimizzazione.
L'algoritmo del simplesso massimizza o minimizza una funzione lineare, detta funzione obiettivo, considerando i vincoli sulle variabili decisionali del modello di ottimizzazione.
Un esempio pratico
Ho un problema di ottimizzazione.
$$ \begin{cases} \min z(x)=-3x_1 -x_2 + 2x_3 \\ \\ x_1 \le 2 \\ x_1+x_2+x_3 = 6 \\ 3x_1 + 2x_3 = 10 \\ \\ x_1, x_2, x_3 \ge 0 \end{cases} $$
Lo trasformo in forma standard.
$$ \begin{cases} \min z(x)=-3x_1 -x_2 + 2x_3 \\ \\ x_1 +x_4 = 2 \\ x_1+x_2+x_3 = 6 \\ 3x_1 + 2x_3 = 10 \\ \\ x_1, x_2, x_3, x_4 \ge 0 \end{cases} $$
La matrice dei coefficienti è
$$ A = \begin{pmatrix} 1 & 0 & 0 & 1 \\ 1 & 1 & 1 & 0 \\ 3 & 0 & 2 & 0 \end{pmatrix} $$
Il rango r(A) è uguale a 3.
Il rango r(A) ed è uguale a r(A|B), secondo il teorema di Rouché-Capelli ha una o più soluzioni.
Scelgo tre vettori linearmente indipendenti per formare una base.
Ad esempio, le colonne 2, 3 e 4 che per semplicità indico con [2,3,4].
$$ A_B = \begin{pmatrix} 0 & 0 & 1 \\ 1 & 1 & 0 \\ 0 & 2 & 0 \end{pmatrix} $$
Le variabili escluse dalla selezione (x1) sono poste a zero.
Poi verifico se è una base ammissibile.
$$ x_B = A_B^{-1} b $$
$$ x_B = \begin{pmatrix} 0 & 0 & 1 \\ 1 & 1 & 0 \\ 0 & 2 & 0 \end{pmatrix}^{-1} \begin{pmatrix} 2 \\ 6 \\ 10 \end{pmatrix} $$
$$ x_B = \begin{pmatrix} 0 & 1 & -0.5 \\ 0 & 0 & 0.5 \\ 1 & 0 & 0 \end{pmatrix} \begin{pmatrix} 2 \\ 6 \\ 10 \end{pmatrix} $$
$$ x_B = \begin{pmatrix} 1 \\ 5 \\ 2 \end{pmatrix} $$
Questa base assegna alle variabili della base x2=1, x3=5, x4=2.
E' una soluzione di base ammissibile perché, secondo i vincoli del problema, le variabili x2, x3, x4 ≥ 0.
In corrispondenza di questi valori la funzione obiettivo del modello assume il valore
$$ \min z(x)=-3x_1 -x_2+2x_3 $$
$$ \min z(x)=-3(0) -(1)+2(5) $$
$$ \min z(x)= -1 + 10 $$
$$ \min z(x)= 9 $$
Ora trasformo il modello in una forma canonica rispetto alla base [2,3,4]
$$ \begin{cases} \min c_B^T A_B^{-1}b + c_N^T x_N \\ x_B = A_B^{-1}b - A_B^{-1} A_N x_N \\ x_B,x_N \ge 0 \end{cases} $$
$$ \begin{cases} \min \begin{pmatrix} -2 \\ 1 \\ 0 \end{pmatrix} \begin{pmatrix} 1 \\ 5 \\ 2 \end{pmatrix} + c_N^T x_N \\ \begin{pmatrix} x_2 \\ x_3 \\ x_4 \end{pmatrix} = \begin{pmatrix} 1 \\ 5 \\ 2 \end{pmatrix} - \begin{pmatrix} 0 & 1 & -0.5 \\ 0 & 0 & 0.5 \\ 1 & 0 & 0 \end{pmatrix} A_N x_N \\ x_B,x_N \ge 0 \end{cases} $$
$$ \begin{cases} \min 9 + c_N^T x_N \\ \begin{pmatrix} x_2 \\ x_3 \\ x_4 \end{pmatrix} = \begin{pmatrix} 1 \\ 5 \\ 2 \end{pmatrix} - \begin{pmatrix} 0 & 1 & -0.5 \\ 0 & 0 & 0.5 \\ 1 & 0 & 0 \end{pmatrix} A_N x_N \\ x_B,x_N \ge 0 \end{cases} $$
Aggiungo i coefficienti AN delle variabili escluse dalla base.
In questo caso è solo la x1.
$$ \begin{cases} \min 9 + c_N^T x_N \\ \begin{pmatrix} x_2 \\ x_3 \\ x_4 \end{pmatrix} = \begin{pmatrix} 1 \\ 5 \\ 2 \end{pmatrix} - \begin{pmatrix} 0 & 1 & -0.5 \\ 0 & 0 & 0.5 \\ 1 & 0 & 0 \end{pmatrix} \begin{pmatrix} 1 \\ 1 \\ 3 \end{pmatrix} \begin{pmatrix} x_1 \end{pmatrix} \\ x_B,x_N \ge 0 \end{cases} $$
Poi svolgo i calcoli.
$$ \begin{cases} 9 + c_N^T x_N \\ \begin{pmatrix} x_2 \\ x_3 \\ x_4 \end{pmatrix} = \begin{pmatrix} 1 \\ 5 \\ 2 \end{pmatrix} - \begin{pmatrix} -0.5 \\ 1.5 \\ 1 \end{pmatrix} \begin{pmatrix} x_1 \end{pmatrix} \\ x_B,x_N \ge 0 \end{cases} $$
Trasformo l'equazione vettoriale in parametrica
$$ \begin{cases} \min 9 + c_N^T x_N \\ \\ x_2 = 1 + 0.5 x_1 \\ x_3 = 5 - 1.5 x_1 \\ x_4 = 2 - x_1 \\ \\ x_B,x_N \ge 0 \end{cases} $$
Poi calcolo i costi cN delle variabili escluse xN dalla base.
$$ c - c_B A^{-1}_B A $$
$$ ( -3 , -1 , 2 , 0 ) - ( -1, 2, 0 ) \begin{pmatrix} 0 & 1 & -0.5 \\ 0 & 0 & 0.5 \\ 1 & 0 & 0 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 1 \\ 1 & 1 & 1 & 0 \\ 3 & 0 & 2 & 0 \end{pmatrix} $$
$$ ( -3 , -1 , 2 , 0 ) - ( -1, 2, 0 ) \begin{pmatrix} -0.5 & 1 & 0 & 0 \\ 1.5 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 \end{pmatrix} $$
$$ ( -3 , -1 , 2 , 0 ) - ( 3.5, -1, 2, 0 ) $$
$$ ( -6.5 , 0 , 0 , 0 ) $$
Ho così' trovato il costo (c1=-6.5) delle variabili escluse xN.
Nota. Quando tutti i coefficienti di costo sono maggiori o uguali a zero si tratta di un ottimo. L'algoritmo cessa la ricerca delle soluzioni in altre SBA ammissibili. In questo caso, un coefficiente è negativo. Pertanto, non è un ottimo.
Ora sostituisco i valori nel modello in forma canonica.
$$ \begin{cases} \min 9 + c_N^T x_N \\ \\ x_2 = 1 + 0.5 x_1 \\ x_3 = 5 - 1.5 x_1 \\ x_4 = 2 - x_1 \\ \\ x_B,x_N \ge 0 \end{cases} $$
$$ \begin{cases} \min 9 - 6.5 x_1 \\ \\ x_2 = 1 + 0.5 x_1 \\ x_3 = 5 - 1.5 x_1 \\ x_4 = 2 - x_1 \\ \\ x_1,x_2,x_3,x_4 \ge 0 \end{cases} $$
A questo punto assegno un valore nullo a tutte le variabili escluse xN.
Quindi x1=0.
$$ x_N = 0 $$
Infine, aspetto importante da non dimenticare, sposto i termini noti dei vincoli a destra e tutto il resto a sinistra.
$$ \begin{cases} \min 9 - 6.5 x_1 \\ \\ x_2 - 0.5 x_1 = 1 \\ x_3 + 1.5 x_1 = 5 \\ x_4 + x_1 = 2 \\ \\ x_1,x_2,x_3,x_4 \ge 0 \end{cases} $$
A questo punto seleziono una variabile della funzione obiettivo con coefficiente che mi permetta di ridurla più rapidamente.
E' la variabile x1 perché ha coefficiente -6.5.
$$ \min z(x)=- \min 9 - 6.5 x_1 $$
Essendo la prima variabile memorizzo nella variabile k il numero 1.
$$ k=1 $$
Questo però non basta devo anche verificare che la variabile compaia nel sistema e abbia almeno un coefficiente maggiore di zero.
Nota. Se nelle equazioni dei vincoli tutti i coefficienti della variabile sono negativi, la ricerca delle soluzioni termina qui perché si tratta di un problema illimitato.
In questo caso la variabile x1 ha coefficiente positivo nella seconda e terza equazione.
$$ \begin{cases} x_2 - 0.5 x_1 = 1 \\ x_3 + 1.5 x_1 = 5 \\ x_4 + x_1 = 2 \end{cases} $$
Quale variabile far uscire dalla base?
Ora cerco la variabile da far uscire dal sistema usando questa formula.
$$ h = \arg \min ( \frac{b_i}{a_{ik}}: a_{ik} \ge 0) $$
Dove il valore h è l'indice dell'equazione del modello in cui si trova il coefficiente, ossia il numero di riga.
In pratica, cerco l'equazione in cui il coefficiente a1 della x1 è positivo e il rapporto bi/ai1 è più basso.
Considerando le equazioni dei vincoli $$ \begin{cases} x_2 - 0.5 x_1 = 1 \\ x_3 + 1.5 x_1 = 5 \\ x_4 + x_1 = 2 \end{cases} $$
Il rapporto b\a è il seguente:
$$ h = \arg \min ( \frac{5}{1.5} , \frac{2}{1}: a_{ik} \ge 0) $$
$$ h = \arg \min ( \frac{2}{1}: a_{ik} \ge 0) $$
$$ h = \arg ( 2 ) $$
Il valore minimo x1=2 si trova nella terza equazione (h=3) che determina la variabile di base x4.
$$ h = \arg ( 2 ) = 3 $$
Ho così trovato il nuovo valore della variabile x1 (entrante in base) e la variabile x4 da far uscire dalla base [2,3,4]
$$ x_1 = 2 $$ $$ h = 3 $$
Nota. La colonna uscente dalla base [2,3,4] è quella con indice 4 ossia la variabile x4 perché il rapporto b/a positivo minimo si trova nella terza equazione (h=3) del modello che determina la variabile x4.
La base successiva da considerare passa da [2,3,4] a [2,3,1] dove la variabile x1 sostituisce la variabile x4.
E indirettamente ho trovato anche il costo z(x) della funzione obiettivo.
$$ \min z(x)= \min 9 - 6.5 x_1 $$
$$ \min z(x)= \min 9 - 6.5 (2) $$
$$ z(x)= -4 $$
Sostituendo la variabile x1 nel sistema, ottengo anche il valore delle variabili della base [2,3,1].
$$ \begin{cases} x_2 = 1 + 0.5 x_1 \\ x_3 = 5 - 1.5 x_1 \\ x_4 = 2 - x_1 \end{cases} $$
$$ \begin{cases} x_2 = 1 + 0.5 (2) \\ x_3 = 5 - 1.5 (2) \\ x_4 = 2 - (2) \end{cases} $$
$$ \begin{cases} x_2 = 2 \\ x_3 = 2 \\ x_4 = 0 \end{cases} $$
Pertanto, i valori delle variabili decisionali sono:
$$ x = ( x_1, x_2, x_3, x_4) = ( 2, 2, 2, 0 ) $$
La nuova base da considerare è [2,3,1].
Ora devo trasformare il modello in una forma canonica rispetto alla nuova base [2,3,1]. tramite un'operazione pivot sul coefficiente ah,k ossia a3,1.
Per prima cosa costruisco la seguente matrice
$$ \begin{pmatrix} -d & c \\ b & A \end{pmatrix} $$
Dove d è il termine noto della funzione obiettivo mentre b è quello dei vincoli, mentre c è il vettore dei coefficienti di costo e A la matrice dei coefficienti.
$$ \begin{cases} \min 9 - 6.5 x_1 \\ \\ x_2 - 0.5 x_1 = 1 \\ x_3 + 1.5 x_1 = 5 \\ x_4 + x_1 = 2 \\ \\ x_1,x_2,x_3,x_4 \ge 0 \end{cases} $$
Quindi
$$ \begin{pmatrix} -9 & -6.5 & 0 & 0 & 0 \\ 1 & -0.5 & 1 & 0 & 0 \\ 5 & 1.5 & 0 & 1 & 0 \\ 2 & 1 & 0 & 0 & 1 \end{pmatrix} $$
La prima riga e la prima colonna hanno indice uguale a zero.
L'elemento pivot ah,k = a3,1 = 1
Divido la riga h=3 per il pivot a3,1.
$$ \begin{pmatrix} -9 & -6.5 & 0 & 0 & 0 \\ 1 & -0.5 & 1 & 0 & 0 \\ 5 & 1.5 & 0 & 1 & 0 \\ \frac{2}{1} & \frac{1}{1} & \frac{0}{1} & \frac{0}{1} & \frac{1}{1} \end{pmatrix} $$
$$ \begin{pmatrix} -9 & -6.5 & 0 & 0 & 0 \\ 1 & -0.5 & 1 & 0 & 0 \\ 5 & 1.5 & 0 & 1 & 0 \\ 2 & 1 & 0 & 0 & 1 \end{pmatrix} $$
Per calcolare le altre righe uso questa formula
$$ a_i - a_{h,k}a_{h}$$
Essendo h=3 e k=1
$$ a_i - a_{3,1}a_1$$
Dove ah=a3 è la riga
$$ ( 2 , 1 , 0 , 0 , 1 ) $$
Quindi la prima riga si calcola
$$ ( -9 , -6.5 , 0 ,0 , 0 ) - (-6.5) ( 2 ,1 , 0 , 0 , 1 ) $$
$$ ( -9 , -6.5 , 0 ,0 , 0 ) - ( -13 , -6.5 , 0 , 0 , -6.5 ) $$
$$ ( 4 , 0 , 0 ,0 , 6.5 ) $$
La seconda riga
$$ ( 1 , 0.5 , 1 ,0 , 0 ) - (-0.5) ( 2 ,1 , 0 , 0 , 1 ) $$
$$ ( 1 , 0.5 , 1 ,0 , 0 ) - ( -1 , -0.5 , 0 , 0 , -0.5 ) $$
$$ ( 2 , 0 , 1 ,0 , 0.5 ) $$
La terza riga diventa
$$ ( 5 , 1.5 , 0 , 1 , 0 ) - (1.5) (2 ,1 , 0 , 0 , 1 ) $$
$$ ( 5 , 1.5 , 0 , 1 , 0 ) - ( 3 , 1.5 , 0 , 0 , 1.5 ) $$
$$ ( 2 , 0 , 0 , 1 , -1.5 ) $$
La quarta riga è quella dell'elemento pivot ed è già stata calcolata.
Dopo queste modifiche la nuova matrice è
$$ \begin{pmatrix} 4 & 0 & 0 & 0 & 6.5\\ 2 & 0 & 1 & 0 & 0.5 \\ 2 & 0 & 0 & 1 & -1.5 \\ 2 & 1 & 0 & 0 & 1 \end{pmatrix} $$
Nota. Per raggiungere lo stesso risultato avrei potuto usare la matrice pivot. E' forse il metodo più semplice, secondo me, per calcolare il nuovo modello dopo un cambio di base.
che equivale al modello
$$ \begin{cases} \min 4 + 6.5x_4 \\ \\ 2= x_2+0.5x_4 \\ 2=x_3-1.5x_4 \\ 2 = x_1 +x_4 \\ \\ x_1,x_2,x_3,x_4 \ge 0 \end{cases} $$
ossia
$$ \begin{cases} \min 4 + 6.5x_4 \\ \\ x_2+0.5x_4 = 2\\ x_3-1.5x_4 = 2 \\ x_1+x_4 = 2 \\ \\ x_1,x_2,x_3,x_4 \ge 0 \end{cases} $$
E' il modello in forma canonica rispetto alla nuovo base [2,3,1].
Il ciclo ricomincia daccapo e continua finché non si verificano due situazioni
- si trova la soluzione ottimale (tutti i coefficienti di costo sono positivi)
- si stabilisce che il problema è illimitato inferiormente (coefficienti negativi della variabile entrante).
E così via.
Nota. Nel ciclo successivo la soluzione appena trovata x(2,2,2,0) è un ottimo perché la nuova funzione obiettivo 4 + 6.5x4 non ha coefficienti di costo negativi. Quindi, la minimizzazione del problema è z=-4.