Il modello di ottimizzazione
Nella ricerca operativa i problemi sono formalizzati in modelli logico-matematici, detti modelli di ottimizzazione, che aiutano la ricerca della soluzione.
A cosa servono? I modelli di ottimizzazione sono molto utili perché consentono la ricerca automatica della soluzione tramite appositi algoritmi detti risolutori.
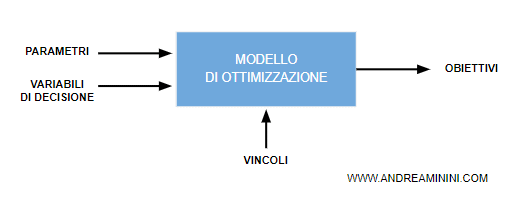
Le caratteristiche di un modello
Un modello di ottimizzazione è un sistema composto da
Gli obiettivi
Un modello ha almeno un obiettivo da raggiungere. Se ha più obiettivi è detto multiobiettivo.
La funzione obiettivo misura l'efficacia delle soluzioni.
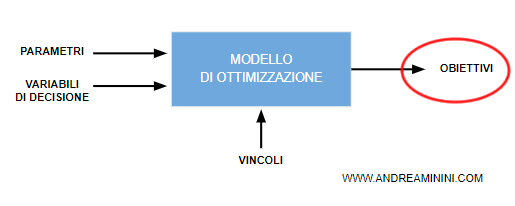
In genere l'obiettivo si presenta come una funzione obiettivo da minimizzare min f(x).
Nota. Non occorre distinguere tra modelli di minimizzazione e massimizzazione. Posso trasformare un obiettivo di minimizzazione min f(x) in uno di massimizzazione, semplicemente ribaltando il segno della funzione min -f(x). Anche l'uguaglianza può essere ottenuta con due condizioni di minimizzazione min f(x)≤y e -min f(x)≤-y .E così via.
La soluzione ammissibile che minimizza la funzione obiettivo è detta soluzione ottima.
Se invece non esiste alcuna soluzione, il problema è detto inammissibile.
Quando ogni soluzione ammissibile è ottimale, il problema è detto illimitato.
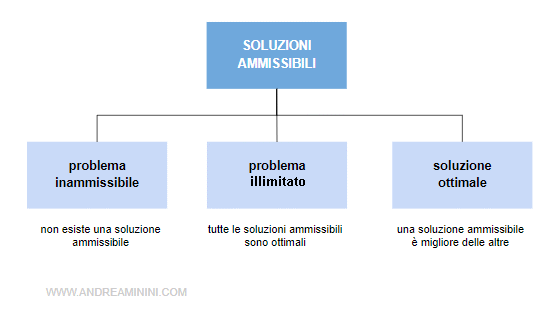
Per un approfondimento rimando alla lettura delle soluzioni del problema di ottimizzazione.
Nota. Se un modello non ha obiettivi da raggiungere, qualsiasi soluzione ammissibile va bene per risolvere il problema.
Le variabili
Un sistema è composto da due tipologie di variabili
- Parametri. Sono variabili esogene che descrivono i dati del problema. Non sono modificabili dall'agente decisore.
- Variabili di decisione. Sono variabili endogene del sistema che formalizzano la decisione per risolvere il problema. Sono controllabili dall'agente decisore.
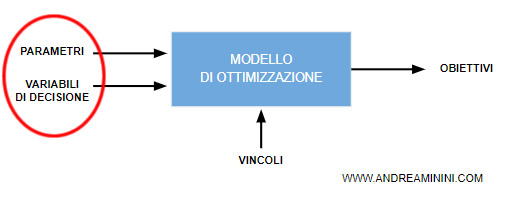
Generalmente, in un modello di ottimizzazione le variabili di decisione sono indicate con la lettera x.
xi
Dove i è l'indice delle variabili del modello i=1...n
Tipi di variabili
In un modello esistono diverse tipologie di variabili
- Variabili intere. Le variabili intere possono assumere soltanto valori discreti nell'insieme dei numeri interi Z. Ad esempio, la variabile decisionale può assumere i valori [0,1,2,3,4,5]. Sono alla base della cosiddetta "programmazione intera" ( PI ).
- Variabili reali. Le variabili reali possono assumere valori reali R continui o non continui. Ad esempio, la variabile decisionale può assumere valori nel range da 0 a 5. Quindi, anche i valori decimali come 4.5, 3.11, ecc. Le variabili reali sono alla base della "programmazione lineare" (PL) e della "programmazione non lineare" (NPL).
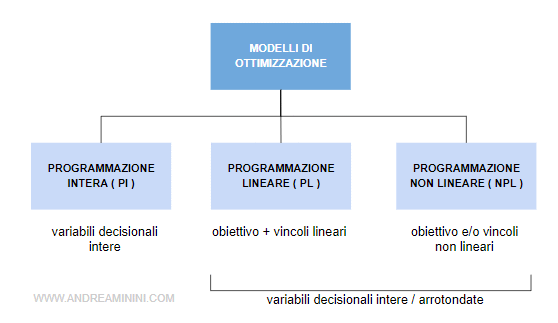
La differenza tra PL e NPL. Nella PL la funzione obiettivo e i vincoli sono funzioni/espressioni lineari. Nella NPL invece la funzione obiettivo e/o alcuni i vincoli sono funzioni/espressioni non lineari. In entrambi i casi, sia nella PL e sia nella NPL, le variabili decisionali x sono reali. Tuttavia, a volte mi conviene arrotondare le variabili a valori interi anche nella PL e nella NPL. Ad esempio, se una funzione obiettivo e vincoli lineari sono usati per decidere un piano di produzione su grandi numeri, non ha senso avere valori decimali per indicare il numero di unità da produrre, in questo caso è opportuno arrotondare ( es. 111,3 automobili diventa 111 automobili ). Il dato è più significativo e non si perde alcuna informazione.
I vincoli
I vincoli sono le condizioni che il modello deve rispettare per trovare le soluzioni.
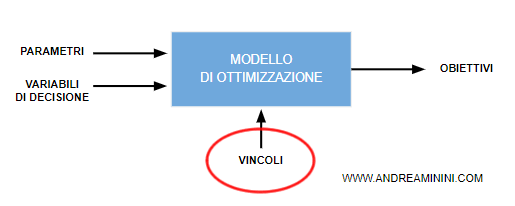
I vincoli riducono l'insieme delle soluzioni ammissibili del problema.
L'insieme di tutte le soluzioni ammissibili è detta regione ammissibile.
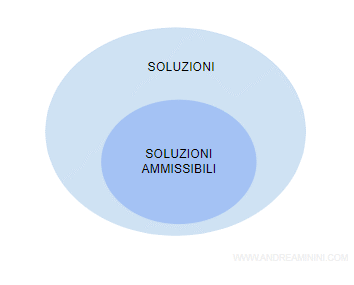
Un modello di ottimizzazione può anche non avere vincoli.
Nota. Se il modello è privo di vincoli, l'insieme delle soluzioni ammissibili ( regione ammissibile ) include tutte le soluzioni possibili.
Dal punto di vista matematico, per rendere più leggibile il modello, posso formalizzare i vincoli usando soltanto l'operatore maggiore-uguale (≥).
vj(x) ≥ αj
Dove v(x) è il vincolo e j è l'indice dei vincoli del modello j=1...m
La variabile α è invece il valore del vincolo da rispettare.
Infatti, qualsiasi relazione può essere trasformata in un vincolo di disuguaglianza.
Esempi
| v(x)≥11 | Maggiore di 10 |
| v(x)≥10 | Maggiore uguale a 10 |
| -v(x)≥-11 | Minore di 10 |
| -v(x)≥-10 | Minore uguale a di 10 |
| -v(x)≥-10 ∪ v(x)≥10 | Uguale a 10 |
E così via
Domande/Risposte
- A cosa serve il modello di ottimizzazione?
Un modello di ottimizzazione trova automaticamente la soluzione a un problema. E' uno strumento della ricerca operativa. - Quali sono le componenti del modello di ottimizzazione?
Un modello di ottimizzazione č composto da obiettivi, vincoli e variabili. - Quali sono le variabili del modello?
Le variabili del modello sono i parametri (esogene) e le variabili decisionali (endogene) - Un modello puņ essere privo di vincoli?
Si, un modello puņ anche non avere vincoli. In questo caso l'insieme delle soluzioni ammissibili comprende tutte le soluzioni possibili del problema - Cos'č la soluzione ottimale?
E' la soluzione che minimizza la funzione obiettivo. E' la migliore possibile tra le soluzioni ammissibili - Un modello puņ essere privo di obiettivo?
Si, un modello puņ anche non avere un obiettivo. In questo caso, qualsiasi soluzione ammissibile va bene per risolvere il problema
