Neuroni artificiali
In informatica i neuroni artificiali sono le unità di base delle reti neurali artificiali. Sono utilizzati nel machine learning e nell'intelligenza artificiale.
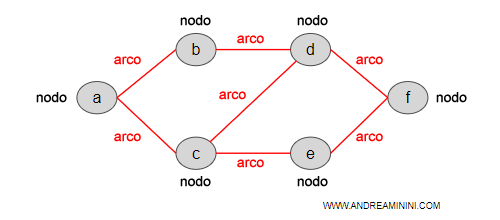
Cos'è una rete neurale artificiale? E' uno strumento informatico usato come classificatore oppure come modello di simulazione del cervello. Una rete neurale è ben rappresentata con un grafo composto da nodi e archi ed è simile al cervello umano dove i neuroni sono collegati tra loro dalle sinapsi.
La storia
Il concetto di neurone artificiale nacque nel 1943, quando Warren McCullok e Walter Pitts costruirono un modello biofisico per spiegare il funzionamento delle cellule nervose (neuroni) del cervello umano.
Lo studio è "A Logical Calculus of the Ideas Immanent in Nervous Activity. The bulletin of mathematical biophysics", 5:4 , 115-133, 1943
In biologia un neurone è un unità computazionale elementare composta da dendriti, soma e assoni.

- I dendriti sono i recettori (x). Sono i collegamenti di entrata ( input ) in cui arrivano i segnali esterni e le informazioni ( micro scariche elettriche ) provenienti dagli altri neuroni.
- La soma è il corpo cellulare del neurone. Riceve i segnali dai recettori e li elabora per prendere una decisione da trasmettere agli effettori. Quando le scariche elettriche superano una certa soglia minima, detta potenziale di azione, il neurone si eccita e trasmette un segnale diverso agli effettori.
- Gli assoni sono gli effettori (y). Sono i collegamenti di uscita ( output ) tramite i quali il neurone invia i segnali verso l'esterno e gli altri neuroni.
Le sinapsi ( dendriti e assoni ) hanno un peso sinaptico (w) che varia nel tempo.
Non è mai lo stesso.
Esempio. A parità di scarica elettrica in entrata, una stessa sinapsi potrebbe avere un peso wt1 nell'istante t1 e wt2 nell'istante t2. Pertanto, in momenti e pesi diversi, la stessa sinapsi fa passare una scarica elettrica differente. Questa variabilità dei pesi sinaptici consente al cervello la funzione plastica di adattarsi alle situazioni esterne.
I pesi sinaptici sono dette:
- sinapsi eccitatorie se w>0
- sinapsi attenuatrici se 0<w<1
- sinapsi amplificatrici se w>1
- sinapsi inibitorie se w<0
Il modello MCP
Lo studio di McCullock-Pitts fu ripreso nel 1957 da Frank Rosenblatt per costruire un modello più evoluto basato sugli stessi principi di funzionamento.
Lo studio di Rosenblatt è "The Perceptron, a Perceiving and Recognizing Automaton", Cornell Aeronautical Laboratory, 1957
Questo modello è detto neurone MCP ( McCullock, Pitts, Rosenblatt ).
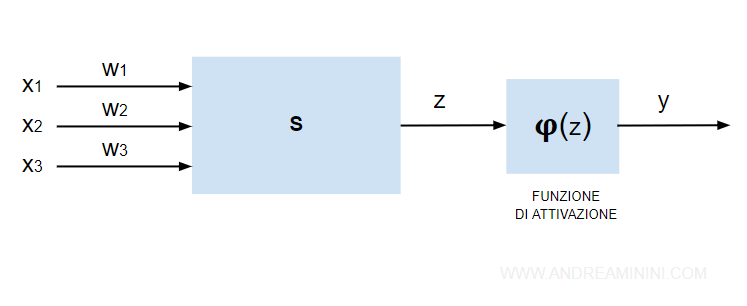
Il segnale in uscita (z) dal sommatore è detto potenziale di attivazione.
Nel neurone MCP il segnale in output (y) è limitato da una funzione di attivazione φ(z).
La funzione φ(z) assume due valori a seconda del valore di z.

La funzione di attivazione è una funzione a gradini ( o funzione di passo ).
Pertanto, è una funzione non lineare.

Il sistema centrale S ( Sommatore ) somma tra loro i vari segnali di input (x) per i relativi pesi (w).

Il neurone MCP è un modello non lineare. Una componente del modello è lineare ( funzione somma o sommatore ) mentre un'altra è non lineare ( funzione di attivazione ). Pertanto, complessivamente il neurone MCP è un modello non lineare.
Nel modello MCP il neurone trasmette all'esterno un segnale, quando il segnale accumulato supera una certa soglia.
Questa regola di apprendimento detta perceptron.
Il modello di Rosenblatt può essere usato nelle attività di machine learning per risolvere i problemi di classificazione.
L'algoritmo Perceptron
L'algoritmo di apprendimento del neurone MCP di Rosenblatt è il Perceptron.
Come funziona
Inizialmente assegno il valore zero oppure un valore infinitesimale molto basso a tutti i pesi w del neurone.

Poi eseguo l'algoritmo di apprendimento del perceptron.
- Calcolo l'output y del neurone in base ai vettori X e W attuali

- Aggiorno il vettore dei pesi (W) del neurone tramite la regola di aggiornamento dei pesi del perceptron

Nota. La variabile y è l'output della funzione di attivazione del neurone ( etichetta calcolata ). La variabile y* è l'etichetta corretta dell'esempio di apprendimento, quella che il neurone dovrà imparare a restituire. La variabile x è il valore in input dell'i-esimo dendrite. La costante η è una costante di apprendimento assegnata a un valore compreso tra 0 e 1.
- Reiterazione del processo per N epoch. Il processo di apprendimento torna al punto (1) e viene ripetuto per N cicli ( epoch ).
Un esempio pratico
L'algoritmo deve risolvere un problema di classificazione binaria ( due classi ).
Le classi sono +1 e -1.

Il modello MCP è un sistema non lineare
Il sistema può essere semplificato e riscritto in questa forma:

Ora posso riscrivere il sistema in forma più semplice ponendo z>0 come condizione della funzione di attivazione.

Quindi, se il valore di soglia è uguale a due ( θ = 2 ) la funzione di attivazione diventa:

Ora ipotizzo che ci siano soltanto due dendriti ( x1 e x2 ) in entrata sul neurone con i seguenti valori X = { 1, 0 }.
L'etichetta corretta dell'esempio è y*=1.

Il vettore W dei pesi è invece nullo all'inizio.

Per semplicità imposto la costante di apprendimento a uno ( η = 1 )
A questo punto comincia il processo di apprendimento.
Ciclo 1
Nel primo ciclo la sommatoria è uguale a z=-2.
Quindi la funzione di attivazione è φ= -1 perché non si verifica z>0.

Essendosi verificato un errore di previsione ( y* - y ) ≠ 0 , il perceptron ricalcola i pesi W degli input. Ora w1=2.

Il neurone restituisce l'etichetta -1 .
Ciclo 2
Nel secondo ciclo la sommatoria è uguale a z=0.
La funzione di attivazione è ancora φ= -1 perché non si verifica z>0.

Il perceptron aggiorna di nuovo i pesi sinaptici. Ora w1=4.

Il neurone restituisce l'etichetta -1 .
Ciclo 3
Nella terza iterazione z=2.
Poiché z>0, ora la funzione di attivazione φ= 1.

In questa iterazione il perceptron non aggiorna i pesi sinaptici (W) perché non c'è alcun errore di previsione.
Ora il neurone classifica l'esempio con l'etichetta corretta ( y = y* = 1 ).

L'algoritmo perceptron ha modificato i pesi sinaptici addestrando il neurone a classificare l'esempio con l'etichetta corretta.
In un problema di classificazione supervisionata lo stesso processo di apprendimento è eseguito in ogni ciclo su tutti gli N nodi della rete neurale.

Dopo k cicli il perceptron trova l'equilibrio su tutti i nodi ( neuroni ) se le etichette sono separabili in modo lineare.
In una condizione di equilibrio generale nessun neurone modifica più i pesi W dei suoi dendriti.
E così via.
Il parametro epoch
Se la classificazione dei dati non è lineare, l'algoritmo Perceptron entra in un loop infinito.
A ogni ciclo almeno un neurone a cambia i propri pesi W.

In questo caso la rete neurale non raggiungerà mai l'equilibrio generale dei neuroni.
Per questa ragione, prima di elaborare il perceptron fisso un numero massimo di reiterazioni detto epoch.
Se la rete neurale non raggiunge l'equilibrio generale dopo K cicli ( epoch ), il perceptron restituisce il modello con l'equilibrio parziale più efficace.
In questo modo l'algoritmo evita il loop infinito, restituendo comunque un modello predittivo accettabile.
