La programmazione lineare

Cos'è la programmazione lineare? La programmazione lineare (PL) risolve problemi di ottimizzazione nei modelli in cui la funzione obiettivo e i vincoli sono espressioni lineari e le variabili di decisione sono reali.

E' uno dei metodi di ottimizzazione alla base della ricerca operativa.

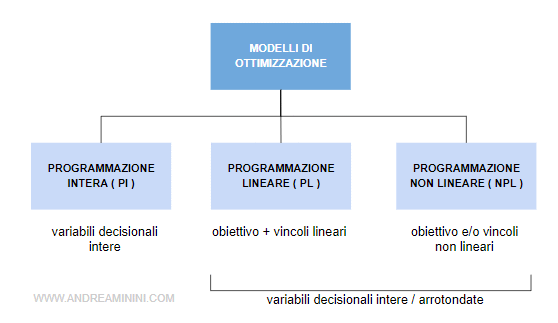
Si distingue dalla programmazione non lineare ( NPL ) e dalla programmazione intera ( PI ).

Qual è la differenza tra programmazione lineare, non lineare e intera? La programmazione non lineare ( NPL ) ha una funzione obiettivo e/o almeno un vincolo non lineare. La programmazione intera ( PI ), invece, usa variabili decisionali di tipo intero.

Il modello di ottimizzazione lineare

Un modello di ottimizzazione lineare consiste in tre elementi

• Funzione obiettivo

  min f(x) = c₁x₁ + ... + c_nx_n

  Dove c = coefficienti di costo della funzione obiettivo e x = variabili decisionali
• Variabili decisionali

  x₁,...,x_n

  Nella programmazione lineare le variabili decisionali possono essere reali o intere arrotondate.
• Vincoli del problema

  v_i = α₁x₁ + ... + α_nx_n ≥ b_i con i=1,...,m

  Dove α = coefficienti tecnologici e b = termini noti dei vincoli ( o risorse )

Non necessariamente devono esserci tutti e tre.

Pertanto, un modello è composto da n variabili decisionali (x), n coefficienti di costo (c), m vincoli (v), m coefficienti tecnologici (α) e m termini noti (b).

Nota. Per semplicità ipotizzo che il modello di ottimizzazione abbia un solo obiettivo da raggiungere. In realtà, un modello PL potrebbe avere anche due o più obiettivi ( modelli multiobiettivo ). La spiegazione però si complicherebbe inutilmente.

Posso formalizzare il modello in forma matematica tramite un sistema lineare.

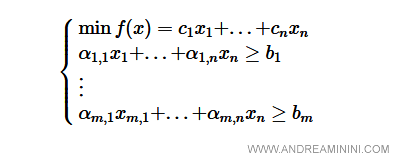
A sua volta posso rappresentare il sistema lineare in una forma matriciale e vettoriale più compatta

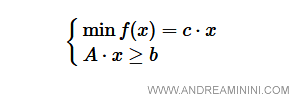
In questo caso le lettere minuscole indicano dei vettori e le lettere maiuscole delle matrici.

• c = vettore dei coefficienti [ c₁,...,c_n ]
• x = vettore delle variabili decisionali [ x₁,...,x_n ]
• b = vettore delle risorse / termini noti [ b₁,...,b_n ]
• A = matrice dei coefficienti tecnologici

Quindi

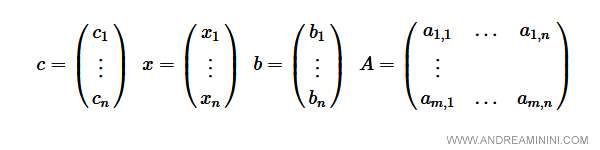
Per completezza aggiungo anche un vincolo di non negatività delle variabili decisionali ( x ≥ 0 ).

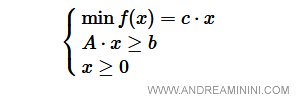
L'arrotondamento delle variabili di decisione

In un modello PL le variabili di decisione (x) sono generalmente di tipo reale.

Tuttavia, posso comunque arrotondare le variabili di decisione a valori interi se necessario.

Se la scala è molto grande, non si perde alcuna informazione e il valore intero è più significativo di quello reale.

Esempio. Se devo decidere la produzione mensile di matite, non ha senso fissarlo a un valore reale ( es. 120,4 matite ). In questi casi è meglio arrotondarlo a un valore intero ( es. 120 matite ).

Viceversa, se il range di variazione delle variabili decisionali è molto piccolo, è meglio evitare l'arrotondamento perché la perdita di informazioni potrebbe diventare eccessiva.

Esempio. Se devo decidere il margine di rischio di un investimento ( es. 3.44% ), arrotondare questo valore ( 3% ) implica una notevole perdita di informazione perché, una volta moltiplicato per il capitale investito, può causare enormi differenze. In questi casi è meglio evitare l'arrotondamento.

In conclusione, si può usare un modello di programmazione lineare anche con variabili intere arrotondate.

Il funzionamento è sempre lo stesso.

E così via.