Come scrivere un problema di programmazione lineare
Per scrivere un problema di programmazione lineare devo
- Analizzare i dati del problema
- Trovare le variabili
- Trovare i vincoli
- Scrivere la funzione obiettivo
A parte l'analisi iniziale dei dati, i passi successivi possono avvenire in ordine diverso.
Ad esempio, a volte l'obiettivo del problema è subito chiaro e aiuta a trovare le variabili. Altre volte sono i vincoli a chiarire subito quali siano le variabili del problema.
Un esempio pratico
Un progetto è composto da 14 attività.
Ogni attività ha una durata certa ed eventualmente dei vincoli di precedenza con altre attività.
Devo individuare la durata minima del progetto.
| Attività | Durata | Attività precedenti |
|---|---|---|
| A1 | 3 | -- |
| A2 | 8 | -- |
| A3 | 9 | A1 |
| A4 | 9 | A1 |
| A5 | 12 | A1 |
| A6 | 7 | A1, A2, A3 |
| A7 | 4 | A5 |
| A8 | 8 | A7, A6 |
| A9 | 6 | A3, A5 |
| A10 | 10 | A4, A7 |
| A11 | 6 | A9 |
| A12 | 4 | A9, A11 |
| A13 | 17 | A2 |
| A14 | 3 | A9, A13 |
Lo scopo è la durata del progetto.
Poiché ogni attività ha una durata certa (costanti).
Quello che io posso decidere sono gli istanti di inizio delle attività nel tempo.
Gli istanti di tempo di inizio attività sono le variabili del problema.
$$ x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \\ x_6 \\ x_7 \\ x_8 \\ x_9 \\ x_{10} \\ x_{11} \\ x_{12} \\ x_{13} \\ x_{14} $$
Ad esempio, la variabile x1 indica l'istante in cui inizia l'attività A1, la variabile x2 di A2, ecc.
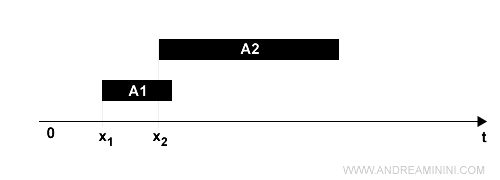
Per ipotesi il tempo comincia da t=0 e, poiché scorre solo in avanti, tutte le variabili devono essere non negative.
Pertanto, aggiungo nel sistema lineare dei vincoli di non negatività alle variabili.
$$ x_1 , x_2 , x_3 , x_4 , x_5 , x_6 , x_7 , x_8 , x_9 , x_{10} , x_{11} , x_{12} , x_{13} , x_{14} \ge 0 $$
Devo però considerare che alcune attività non possono cominciare in qualsiasi istante di tempo, perché devono aspettare che siano finite le attività precedenti a cui sono vincolate.
Ci sono dei vincoli di precedenza da rispettare.
Ad esempio l'attività A3 può cominciare solo dopo che l'attività A1 è finita.
L'attività A1 dura 3 e parte dall'istante x1.
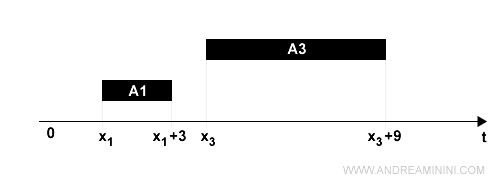
Quindi, l'istante iniziale di A3 ossia x3 deve essere maggiore o uguale alla durata di A1 a partire dal suo istante iniziale x1.
$$ x_3 \ge x_1 + 3 $$
Posso riscrivere la precedente disequazione in questa forma equivalente
$$ x_3 - x_1 \ge 3 $$
E' il primo vincolo di precedenza.
Allo stesso modo posso scrivere tutti i vincoli di precedenza delle attività con predecessore (A3, A4, A5, A6, A7, A8, A9, A10, A11, A12, A13, A14).
$$ x_3 - x_1 \ge 3 \\ x_4 - x_1 \ge 3 \\ x_5 - x_1 \ge 3 \\ x_6 - x_1 \ge 3 \\ x_6 - x_2 \ge 8 \\ x_6 - x_3 \ge 9 \\ x_7 - x_5 \ge 12 \\ x_8 - x_7 \ge 4 \\ x_8 - x_6 \ge 7 \\ x_9 - x_3 \ge 9 \\ x_9 - x_5 \ge 12 \\ x_{10} - x_4 \ge 9 \\ x_{10} - x_7 \ge 4 \\ x_{11} - x_9 \ge 6 \\ x_{12} - x_9 \ge 6 \\ x_{12} - x_{11} \ge 6 \\ x_{13} - x_2 \ge 8 \\ x_{14} - x_9 \ge 6 \\ x_{14} - x_13 \ge 3 $$
Nota. Nelle attività in cui ci sono più predecessori (es. A6, A8, A9, A10, A12, A14) devo scrivere un vincolo per ogni predecessore.
A questo punto resta da capire quando finisce il progetto.
Per indicarlo aggiungo al sistema un'altra variabile di fine progetto.
$$ x_{15} $$
La variabile x15 indica l'istante in cui termina il progetto.
Anche x15 è una variabile di tempo non negativa.
Quindi, aggiungo un ulteriore vincolo di non negatività al sistema
$$ x_{15} \ge 0 $$
Il progetto termina quando tutte le attività sono elaborate.
Tuttavia, sarebbe ridondante verificare che x15 sia superiore alla fine di tutte le 14 attività.
E' sufficiente che lo sia nei confronti delle attività terminali del progetto.
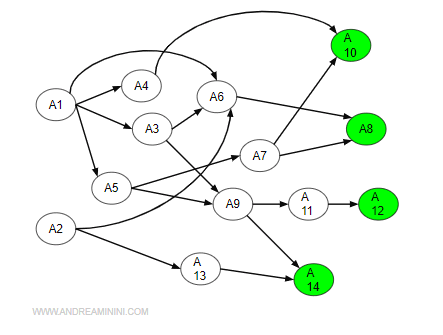
Individuo le attività a cui non seguono altre attività (A8, A10, A12, A14) con i rispettivi tempi iniziali e durate.
Quando sono finite queste attività, il progetto è concluso.
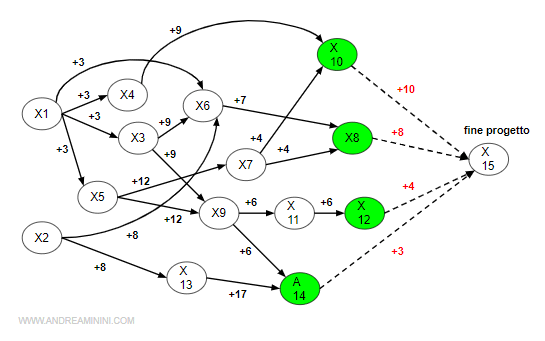
Pertanto, aggiungo altri quattro vincoli di fine progetto al problema
$$ x_{15} - x_8 \ge 8 $$
Nota. Questo vincolo impone che l'istante x15 sia uguale o maggiore all'istante iniziale x8 dell'attività A8 più la sua durata pari a 8.
Ripeto lo stesso ragionamento con le attività A10, A12 e A14
$$ x_{15} - x_{10} \ge 10 $$
$$ x_{15} - x_{12} \ge 4 $$
$$ x_{15} - x_{14} \ge 3 $$
A questo punto mi manca soltanto da definire la funzione obiettivo.
Poiché lo scopo è minimizzare la durata del progetto (x15), la funzione obiettivo è una funzione di minimizzazione di x15
$$ f(z): \: \min \: x_{15} $$
Ho tutti gli elementi per scrivere il problema nella programmazione lineare.
$$ f(z): \: \min \: x_{15} $$
$$ \begin{cases} x_3 - x_1 \ge 3 \\ x_4 - x_1 \ge 3 \\ x_5 - x_1 \ge 3 \\ x_6 - x_1 \ge 3 \\ x_6 - x_2 \ge 8 \\ x_6 - x_3 \ge 9 \\ x_7 - x_5 \ge 12 \\ x_8 - x_7 \ge 4 \\ x_8 - x_6 \ge 7 \\ x_9 - x_3 \ge 9 \\ x_9 - x_5 \ge 12 \\ x_{10} - x_4 \ge 9 \\ x_{10} - x_7 \ge 4 \\ x_{11} - x_9 \ge 6 \\ x_{12} - x_9 \ge 6 \\ x_{12} - x_{11} \ge 6 \\ x_{13} - x_2 \ge 8 \\ x_{14} - x_9 \ge 6 \\ x_{14} - x_13 \ge 3 \\ x_{15} - x_8 \ge 8 \\ x_{15} - x_{10} \ge 10 \\ x_{15} - x_{12} \ge 4 \\ x_{15} - x_{14} \ge 3 \\ x_1 , x_2 , x_3 , x_4 , x_5 , x_6 , x_7 , x_8 , x_9 , x_{10} , x_{11} , x_{12} , x_{13} , x_{14} \ge 0 \end{cases}
Una volta scritto in questa forma posso risolverlo con l'algoritmo del simplesso o altro modo.
E così via.
