Il modello di pianificazione della produzione
Il modello di pianificazione della produzione è un modello di programmazione lineare usato nella ricerca operativa per risolvere problemi di allocazione delle risorse nei processi produttivi.
Cos'è il processo produttivo
Un processo produttivo è un sistema con m input ( risorse ) e n output ( prodotti ).
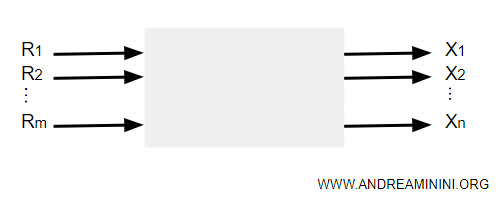
Dove R sono le quantità disponibili delle m risorse e X sono le quantità degli n prodotti.
Esempio. Le risorse ( input ) di un'azienda vinicola sono i macchinari, i lavoratori e le materie prime ( uva ) a disposizione. Gli input sono lavorati per produrre dei prodotti finiti ( es. vino, aceto ) da vendere sul mercato.
Come costruire il modello di pianificazione della produzione
L'azienda decide di produrre le quantità degli n-prodotti.
Sono le variabili decisionali del modello.
$$ x_j \:\:\:\:\:\: j = 1,...,n$$
La produzione di ciascun prodotto non può però essere negativa ( xj ≥ 0 ).
Quindi, le variabili decisionali devono rispettare il vincolo di non negatività.
$$ x_j \ge 0 $$
Per produrre un'unità di un prodotto xi il processo produttivo impiega diverse risorse R ( es. lavoro, materie prime, ecc. ).
La quantità consumata di ogni risorsa per produrre l'i-esimo prodotto è misurata dai coefficienti di produzione aij.
Dove l'indice i indica la risorsa e l'indice j il prodotto.
$$ \begin{array}{c|lcr} & x_1 & ... & x_n \\ \hline R_1 & a_{1,1} & ... & a_{1,n} \\ \vdots & \vdots & & \vdots \\ R_m & a_{m,1} & ... & a_{m,n} \end{array} $$
Poiché l'azienda produce xj unità dello stesso prodotto, consuma aj,n·xj quantità delle risorse.
La quantità impiegata di ogni i-esima risorsa non deve oltrepassare la disponibilità Ri della stessa.
$$ \sum_{j=1}^n a_{i, j} x_j \le R_i $$
Da ciascuna unità di prodotto l'azienda ottiene un profitto pj.
Quindi, il profitto ottenuto producendo xj quantità del j-esimo prodotto è
$$ x_j \cdot p_j $$
Considerando tutti i prodotti, il profitto complessivo dell'azienda è
$$ \sum_{j=1}^n x_j \cdot p_j $$
Uno degli obiettivi di un'impresa privata è la massimizzazione del profitto.
E' la funzione obiettivo del modello.
$$ \max f(x) = \sum_{j=1}^n x_j \cdot p_j $$
Ricapitolando, il modello formale di pianificazione della produzione è il seguente:
$$ \begin{cases} \max f(x) = \sum_{j=1}^n x_j \cdot p_j \\ \\ \sum_{j=1}^n a_{i, j} x_j \le R_i \:\:\:\:\:\: i = 1,...,m \\ \\ x_j \ge 0 \:\:\:\:\:\: j = 1,...,n \end{cases} $$
Un esempio pratico
Esercizio 1
Un'azienda ha 10 lavoratori che, considerando una giornata di lavoro di 8 ore, equivalgono a 80 ore di lavoro al giorno.
Inoltre, ha un approvvigionamento giornaliero di 1000 kg di legno.
Nota. Le ore lavoro e il legno sono le risorse e i relativi vincoli sono 80 e 1000 al giorno.
L'azienda produce tavoli, sedie e sgabelli.
Per costruire i tre prodotti sono necessari tempi di lavorazione e un impiego di legno diversi.
$$ \begin{array}{c|lcr} & Tavolo & Sedia & Sgabello \\ \hline \text{Ore lavoro (h)} & 4 & 1 & 0.5 \\ \text{Legno (kg)} & 30 & 10 & 5 \end{array} $$
Esempio. Per costruire un tavolo sono necessarie 4 ore di lavoro, 1 ora per una sedia e mezz'ora per uno sgabello.
Da ciascuna unità di prodotto ottiene un profitto diverso.
$$ \begin{array}{c|lcr} & Tavolo & Sedia & Sgabello \\ \hline \text{Profitto (€)} & 10 & 5 & 2 \end{array} $$
Esempio. Dalla vendita di un tavolo l'azienda ottiene 10 euro di profitto, 5 euro da una sedia e 2 euro da uno sgabello.
Ora, l'impresa deve pianificare la produzione giornaliera per massimizzare il profitto.
Quanti tavoli, sedie e sgabelli deve produrre?
Formalizzo il problema di ottimizzazione in un modello matematico.
$$ \begin{cases} \max p_1x_1 + p_2x_2 + p_3x_3 \\ \\ 4x_1 + 1x_2 + 0.5x_3 \le 80 \\ 30x_1 + 10x_2 + 5x_3 \le 1000 \\ \\ x_1,x_2,x_3 \ge 0 \end{cases} $$
Dove x1, x2 e x3 sono rispettivamente le quantità di tavoli, sedie e sgabelli da produrre. Sono le variabili decisionali del modello.
Poi lo trasformo in un foglio di calcolo.
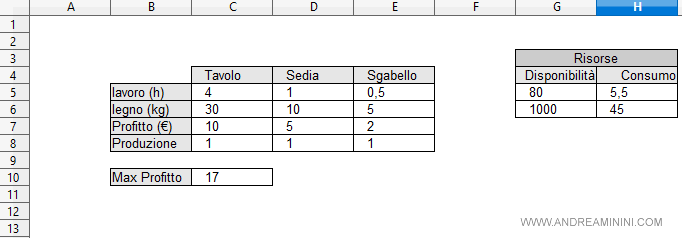
Infine configuro il risolutore del foglio elettronico per trovare la soluzione ottimale del problema.
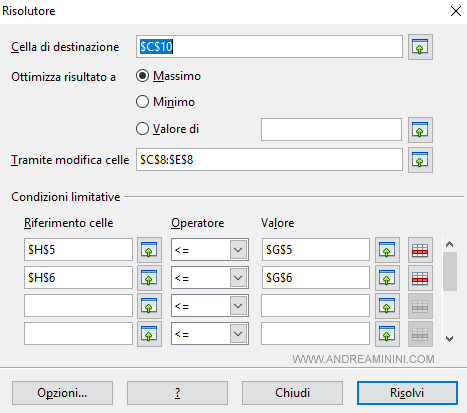
Il risolutore trova la pianificazione ottimale della produzione.
Per massimizzare il profitto l'azienda deve produrre 80 sedie al giorno.
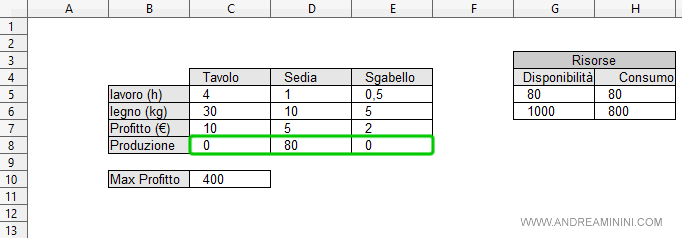
Nota. In questo modo l'azienda ha allocato in modo ottimale le 80 ore di lavoro giornaliere massimizzando il profitto della giornata. La pianificazione riduce il consumo di legno da 1000 (disponibilità max.) a 800.
Esercizio 2
Ora aggiungo un'ipotesi. Ogni giorno l'azienda vende 30 sedie e 50 sgabelli e 1 tavolo.
L'invenduto di sedie e sgabelli va in magazzino, mentre l'invenduto dei tavoli viene venduto ad altre aziende.
$$ \begin{array}{c|lcr} & Tavolo & Sedia & Sgabello \\ \hline \text{Vendite} & 1 & 30 & 50 \end{array} $$
L'azienda deve cercare di limitare l'invenduto in magazzino di sedie e sgabelli.
Al modello aggiungo i vincoli della produzione massima.
$$ \begin{cases} \max p_1x_1 + p_2x_2 + p_3x_3 \\ \\ 4x_1 + 1x_2 + 0.5x_3 \le 80 \\ 30x_1 + 10x_2 + 5x_3 \le 1000 \\ \\ x_1,x_2,x_3 \ge 0 \\ x_2 \le 30 \\ x_3 \le 50 \end{cases} $$
Lo traduco in un modello sul foglio elettronico.
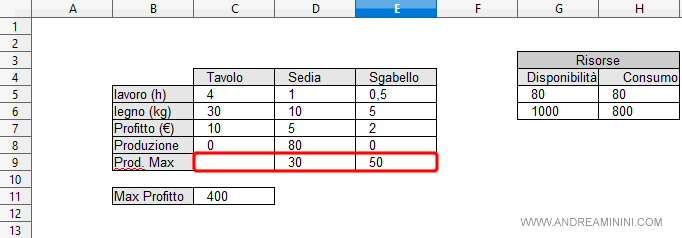
Poi modifico il risolutore aggiungendo i nuovi vincoli.

Nota. La produzione di sedie (D8) deve essere inferiore a 30 (D9) e la produzione di sgabelli (E8) deve essere inferiore a 50 (E9).
Infine, avvio il risolutore per trovare la soluzione ottimale del problema.
Per massimizzare il profitto e limitare l'invenduto in magazzino, l'azienda deve produrre 30 sedie, 50 sgabelli e 6 tavoli ogni giorno.

E così via.
