Come risolvere il problema del cammino orientato al costo minimo
Il problema del cammino orientato al costo minimo è un tipo di problema della programmazione lineare risolvibile con un modello di flusso a rete.
L'obiettivo del modello consiste nel trovare il percorso con minore costo per spostarsi da un nodo iniziale O a un nodo di destinazione Z in un grafo orientato.
E' quindi necessario avere un grafo orientato G(N,A) con un insieme N di nodi e un insieme A di archi.
Dove N è l'insieme dei nodi { 1,2,..., n } e A è l'insieme degli archi { 1,2,...,m }
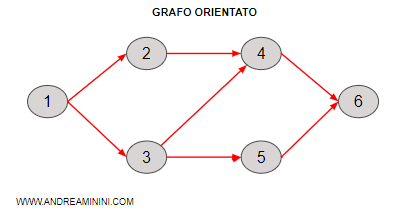
Nota. In questo esempio ho disegnato un grafo orientato con sei nodi e 7 archi. Tutti gli archi hanno una direzione.
A ogni arco è associato un costo cij e una variabile decisionale xij.
Il costo indica il prezzo da pagare per spostarsi dal nodo i al nodo j.
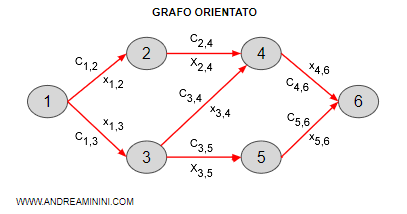
Nota. Gli indici i e j indicano il nodo i-esimo di partenza e il nodo j-esimo di destinazione che l'arco congiunge. Per ipotesi, gli indici devono essere diversi (i≠j) e contigui(j=i+1). Nel caso in cui gli indici possono essere anche uguali ( i=j) non si parla più di cammino ma di percorso.
Se la variabile decisionale xij è maggiore di zero, l'arco fa parte del cammino ottimale.
Viceversa, se la variabile decisionale xij è nulla, l'arco è inutilizzato.
Esempio. Se le variabili decisionali x1,2=x3,5=x5,6=1 e tutte le altre sono uguali a zero, il cammino passa per i nodi 1, 3, 5, 6.
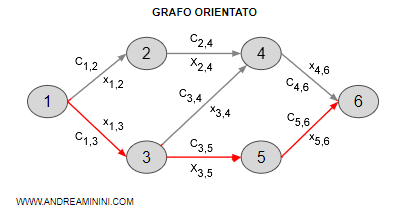
Ogni cammino è una sequenza concatenata di nodi e archi che congiunge il nodo di partenza con quello di destinazione.
A ciascun cammino è associato un costo, pari alla somma dei costi degli archi usati per formare il cammino.
Esempio. Il cammino che passa per i nodi 1,3,5,6 ha un costo pari a $$ C(x) = c_{1,3}+c_{3,5}+c_{5,6} $$
Esistono diversi cammini possibili per congiungere il nodo O con il nodo Z.
Il cammino ottimale è quello che minimizza il costo di spostamento.
$$ \min C(x) = \sum_{(i,j)} c_{i,j} x_{i,j} $$
E' l'obiettivo del modello di ottimizzazione.
Ovviamente, nel modello possono esserci anche dei vincoli che influiscono sulla soluzione ottimale.
Esempio. Un vincolo potrebbe essere quello di evitare il nodo 5. Per farlo devo soltanto imporre nel modello matematico un vincolo con la variabile x3,5 = 0. Per imporre il passaggio nel nodo 4, invece, mi basta inserire il vincolo x2,4 + x3,4 > 0.
Un vincolo molto comune è il vincolo di non negatività delle variabili decisionali.
$$ x_{1,1} , ... , x_{i,j} \ge 0 $$
Nota. Essendo le variabili decisionali di tipo intero e l'obiettivo del modello è la minimizzazione del costo, le variabili decisionali assumono automaticamente il valore più basso possibile, ossia il numero 1 ( attive ) o il numero 0 ( disattive ).
Altri vincoli necessari per il funzionamento della rete sono i vincoli di conservazione del flusso.
$$ \sum_{(i,j)} x_{i,j} - x_{j,i} = b_i $$
Dove bi è la differenza tra gli archi in entrata e in uscita nel nodo i-esimo.
Esempio. Il nodo 2 ha un nodo in entrata e un nodo in uscita. Pertanto, il fattore b del nodo deve essere uguale a 0. E' un nodo di transito. Viceversa, il nodo iniziale ha un fattore b uguale a 1 mentre il nodo terminale a -1.
I vincoli di conservazione del flusso vanno espressi per ciascun nodo.
E così via.
Un esempio pratico
Ho un grafo orientato e devo spostarmi dal nodo 1 al nodo 6.
Il grafo ha i seguenti costi.
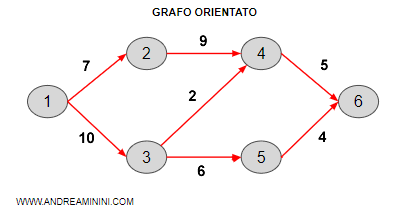
Per trovare il cammino al costo minimo elaboro un modello matematico.

Inserisco i dati nel risolutore del foglio elettronico e calcolo la soluzione.
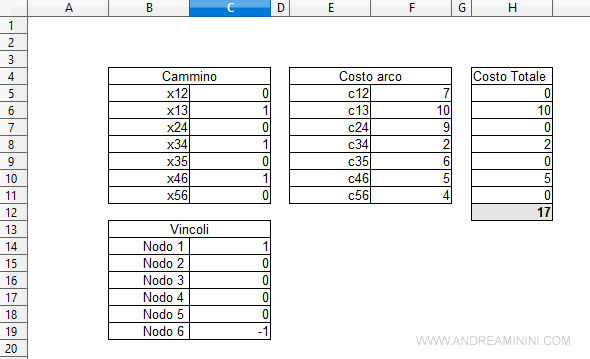
Il cammino minimo è quello che passa per i nodi 1, 3, 4, 6.
Il cammino ha un costo pari a 17 ed è inferiore a tutti i cammini alternativi.
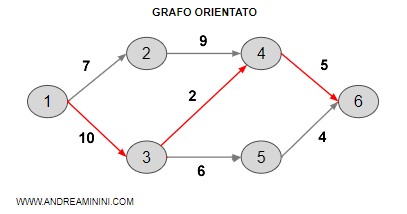
E' la soluzione ottimale del problema.
