Il problema di flusso a costo minimo
Nella ricerca operativa il problema di flusso a costo minimo è uno dei modelli di flusso di rete della programmazione lineare. Questi problemi di ottimizzazione sono rappresentabili tramite una struttura a rete.
Una struttura a rete è composta da un grafo orientato con n nodi e a archi.
$$ G(n,a) $$
L'insieme di tutti i nodi è indicato con la lettera N maiuscola, mentre l'insieme di tutti gli archi con la lettera A.
Ecco un esempio pratico di grafo orientato D(6,8) con 6 nodi e 8 archi.
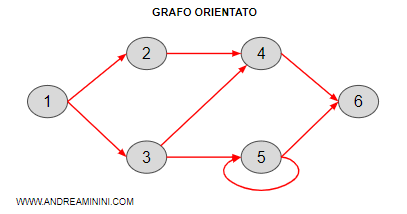
Ogni nodo ha un determinato numero di archi in entrata e in uscita.
La differenza tra gli archi in uscita e in entrata del nodo i è indicata con la variabili bi.
- Se b è negativo ( b<0 ) il nodo è un nodo di domanda
- Se b è positivo ( b>0 ) il nodo è di fornitura
- Se b è nullo ( b = 0 ) il nodo è di transito
Esempio. Nell'esempio precedente il nodo 3 ha un arco in uscita e due archi in entrata, quindi il valore è b3=1-2=-1. Si tratta di un nodo di domanda.
La quantità di flusso in entrata e uscita in ciascun nodo è uguale al valore b del nodo.
Questo vincolo è detto vincolo di conservazione della rete.
Nota. Se il vincolo di conservazione è rispettato, la somma algebrica di tutti i valori b della rete è uguale a zero.
Ogni arco del grafo è indicato con (i,j) dove i e j sono i nodi che congiunge.
$$ a(i,j) $$
Inoltre, ogni arco ha un costo, una capacità minima e massima
- Il costo del passaggio nell'arco (c).
- La capacità è la quantità minima e massima di elementi che possono transitare nell'arco in un determinato periodo di tempo. Sono detti vincoli di capacità degli archi della rete.
$$ min(i,j) \le x_{i,j} \le max(i,j) $$
Esempio. Per comprendere questo concetto è molto utile pensare a un tubo idraulico. La sezione del tubo idraulica determina la portata minima e massima, ossia la quantità d'acqua che può passare nel tubo in un'ora a parità di pressione.
Le variabili decisionali x determinano il flusso negli archi della rete.
Ovviamente, esistono diversi cammini e combinazioni di flusso tra cui scegliere.
L'obiettivo del modello di ottimizzazione consiste nel determinare il flusso tra gli archi con l'obiettivo di minimizzare il costo, tenendo conto degli eventuali vincoli del problema. $$ \min c(x) = \sum_{(i-j) \in A } c_{i,j} x_{i,j} $$
Il costo minimo è il cammino nel grafo con costo totale minore.
E' l'obiettivo del modello di ottimizzazione.
